2. 中国科学院大学, 北京 100049
岩石和土壤都是多重因素交互作用下的产物,具有明显的空间变异特征[1]。充分掌握其空间分布及变化情况是工程设计、土地资源管理等生产实践活动实施精准决策的前提。由于完整空间数据的测量难以实现,学者们将测量数据与数学理论模型相结合,提出了多种空间数据重构方法。
地质统计学(geostatistics)是地学领域主流的空间数据重构方法之一。该方法在二阶平稳假设的基础上,利用样本的空间位置信息计算半方差函数,通过克里格法得到预测点的无偏估计,能够有效避免数据强行拟合多项式产生的边缘效应[2]。然而,实际的地学特性通常不满足二阶平稳假设,而且半方差函数模型的选择和邻域样本数量的定义都具有主观性。半方差函数的质量受到实测数据量及数据采集规则的影响[3],有限的样本数量会降低半方差函数中相关参数的准确性,进而影响重构的精度和有效性[4]。作为表达空间结构的工具,半方差函数仅能把握空间上两点之间的相关性,而无法表征复杂的空间结构和几何形态的地质特征[5]。此外,尽管克里格法提供了方差作为预测点误差和不确定性的度量指标,但由于它与数据值无关,且与估计误差的相关性很差,因此在实际中难以应用[6]。多点地质统计学(multiple-point simulation)是在地质统计学基础上提出的一种随机模拟方法,该方法以马尔科夫随机场(Markov random fields)为支撑,使用“训练图像”代替半方差函数重构空间数据,可以看作是地质学中的标准方法。“训练图像”能够有效描述多点之间的结构性和相关性,克服了传统地统计学在复杂结构特征表征方面的不足,但模拟过程中随机性强,难以控制其模拟效果[7-8]。
为了克服传统方法的不足,探索一种对样本采集要求较低且兼顾数据空间相关性的空间数据重构方法成为地学领域研究的热门方向之一。压缩感知(compressive sensing)[9-12]是21世纪信号处理领域的重大突破,该理论证明:只要信号在原始域或某种变换域中能够被稀疏表达,就可以用一个与变换基不相关的观测矩阵将变换所得高维信号投影到一个低维空间上,然后通过求解优化问题即可从这些少量的投影中以高精度重构出原信号[13]。在压缩感知理论的诸多应用中,基于单像素的图像恢复为空间数据重构提供了新思路。
目前,基于压缩感知的空间数据重构方法已经被应用于流体运动模型的静态参数反演和土力学性质重构的相关研究,并取得了一定的研究成果,然而针对污染物浓度、水盐含量以及养分状况等土壤特性的相关研究尚未展开。本文将在简要介绍压缩感知数学模型的基础上,阐述该方法在地学领域的研究进展,分析该方法在土壤特性空间数据重构中的可行性,并提出几点潜在的研究方向。
1 压缩感知数学理论基础 1.1 信号采集模型压缩感知作为一种全新的信号处理框架,其目标是利用信号的稀疏性或可压缩性减少描述完整信号所需的测量次数[14],其测量过程可以被看作是一个线性投影过程。对于长度为N的稀疏信号X,通过N组长度为M(M
| $ \boldsymbol{Y} = \boldsymbol{\varPhi X} $ | (1) |
值得注意的是,测量过程是非自适应(non- adaptive)的,也就是说,Φ不以任何方式依赖于信号X。
1.2 限制条件 1.2.1 信号稀疏性和可压缩性大多数信号无法满足稀疏性或可压缩性这一基本要求,但通常可以对原始信号进行变换,从而达到这一目的。假设给定一条长度为N的离散信号X,可将其看作N×1维的列向量,记作
| $ \boldsymbol{X} = \sum\limits_{i = 1}^N {{\omega _i}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }} _i} = } \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} \bf{\Omega }$ | (2) |
式中:
整合式(1)、式(2),得到下式:
| $ \mathit{\boldsymbol{Y}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} X}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} \boldsymbol{\varPsi} \boldsymbol{\varOmega} }} = \mathit{\boldsymbol{ \boldsymbol{\varTheta} \boldsymbol{\varOmega} }} $ | (3) |
| $ \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} \boldsymbol{\varPsi} }} $ | (4) |
将矩阵Θ称为感知矩阵,Candès等[10]证明压缩感知框架下信号准确重构的前提条件是Θ符合RIP(restricted isometry property)条件,即任意稀疏信号X∈RN与常数δ∈(0, 1)使得式(5)成立:
| $ (1 - {\delta _K})\left\| \boldsymbol{X} \right\|_2^2 \leqslant \left\| {{\bf{\Theta }} \boldsymbol{X}} \right\|_2^2 \leqslant (1 + {\delta _K})\left\| \boldsymbol{X} \right\|_2^2 $ | (5) |
而Baraniuk等[16]则证明,测量矩阵Φ与稀疏矩阵Ψ不相关是Θ符合RIP条件的等价条件。定义Φ与Ψ之间的相关性为:
| $ \mu (\boldsymbol{\varPhi} ,\mathit{\boldsymbol{ \boldsymbol{\varPsi} }} )\text{=}\sqrt{n}{\cdot }_{1\le i,j\le N}^{\text{max}}\left|\langle {\boldsymbol{\varphi} }_{i}\cdot {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }} }_{j}\rangle \right| $ | (6) |
式中:
压缩感知信号重构过程如下:由测量值Y和感知矩阵Θ,求解方程组Y=ΘΩ,得到稀疏向量Ω*,再由X*=ΨΩ*得到恢复信号。而由于
定义系数向量
| $ {\left\| \boldsymbol{\varOmega} \right\|_p} = (\sum\limits_{i = 1}^N {{{\left| {{\boldsymbol{\omega} _i}} \right|}^p}} )1/p $ | (7) |
当p = 0时,得到0-范数,即Ω中非零项的个数。当信号X满足稀疏或可压缩条件时,可将欠定方程组的求解问题转化为最小化0-范数问题[18]:
| $ {\text{min}}{\left\| {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }} ^T}\boldsymbol{X}} \right\|_0}s.t.\boldsymbol{Y} = \boldsymbol{\varPhi} \mathit{\boldsymbol{ \boldsymbol{\varPsi} \boldsymbol{\varOmega}}} = \mathit{\boldsymbol{ \boldsymbol{\varTheta} \boldsymbol{\varOmega}}} $ | (8) |
求解式(8)的数值计算极不稳定,而且是一个NP难问题,Chen等[19]指出,在Φ和Ψ不相关的前提下,求解相同条件下的L1优化问题能得到与式(8)相同的解,即上式转化为:
| $ \min {\left\| {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }} ^T}\boldsymbol{X}} \right\|_1}s.t.\boldsymbol{Y} = \boldsymbol{\Phi} \mathit{\boldsymbol{ \boldsymbol{\varPsi} \boldsymbol{\varOmega} }} = \mathit{\boldsymbol{ \boldsymbol{\varTheta} \boldsymbol{\varOmega}}} $ | (9) |
在信号满足稀疏性和RIP条件的前提下,原本难以解决的欠定方程组求解被转换为凸优化问题[20],可以将其作为线性规划问题使用BP算法、OMP算法[21]等诸多方法求解。
除满足上述两个要求外,测量矩阵的维数M需要满足式(10)[22]:
| $ \boldsymbol{M} \geqslant C \cdot {\mu ^2}(\mathit{\boldsymbol{ \boldsymbol{\varPsi} }} ,\;\boldsymbol{\varPhi} ) \cdot K \cdot {\text{log}}N $ | (10) |
式中:C > 0为某个固定常数。
2 空间数据重构应用及展望 2.1 流体运动模型的静态参数反演反演问题是石油工程、水文地质等领域建立地下环境流体驱替行为预测数学模型的重要组成部分,主要包含模型参数反演、初始条件反演、边界条件反演、源或汇反演及混合反演5类,其中静态模型参数(储层或含水层水力特性)的反演是主要研究方向[23]。由于未知参数的数量远大于已知的观测数据,这一反演过程是不适定的(Ill-posedness),由此导致反演结果的不稳定性和非唯一性[24]。
2.1.1 反演问题的参数化与正则化为减轻不适定性的影响,参数化(parameterization)和正则化(regularization)被引入反演问题。参数化的目的是减少未知参数的数量,主要有空间域参数化和变换域参数化两种形式。空间域参数化以分区(zonation)为代表,将合并类似区域并为其赋值作为参数化手段,具有较大的局限性[25]。变换域参数化是近年来参数反演研究的新趋势之一,其本质是数据的压缩。在空间相关性的前提下,该方法通过特殊的变换函数将空间域参数投影至变换域,实现模型参数的降维表达,从而有效降低反演过程中的不适定性。参数化变换形式主要有基于协方差的正交分解以及特殊函数两种,前者主要包括截断奇异值分解(TSVD)、主成分分析(PCA)和Karhunen-Loeve变换(KLT)[26-27],后者主要包括离散余弦变换(DCT)和离散小波变换(DWT)[28-29],其中基于特殊函数的变换更加高效且鲁棒性更强。正则化以先验模型、静态数据或参数平滑度等要素对不适定问题的解施加限制,从而稳定不适定问题的解,并约束解在合理条件下再现观测数据[30]。Tikhonov正则化是反演中常用的方法,通过L2范数对解施加约束。此外,在压缩感知理论提出之前,以全变分(total variation)为代表的L1范数约束主要被应用于边缘检测问题和分段平滑特性的重建[31]。
2.1.2 基于压缩感知的反演框架压缩感知的出现,为参数化和正则化的结合提供了理论基础。Jafarpour等[32]将基于参数化和正则化的地质参数反演问题表达为:
| $ \mathop {\arg \min }\limits_{\varOmega \in {R^N}} {\left\| {\boldsymbol{C}_u^{ - 1/2}(\boldsymbol{Y} - \boldsymbol{\varTheta \varOmega} {\text{)}}} \right\|_p} + \lambda {\left\| {\boldsymbol{W\varOmega }} \right\|_q} $ | (11) |
式中:
参数化方法是压缩感知框架下的主要研究内容之一。在使用参数化方法进行反演时,传统方法利用先验信息构建固定的基向量空间,而压缩感知框架下的参数化则是由算法从较大的低频基向量空间中构建出与观测数据相适应的动态子空间。DCT和DWT是压缩感知框架下两种主流的参数化方法,Jafarpour等[33]首先利用DCT验证了压缩感知框架在动态数据集成反演问题中的可行性,随后将DWT与融合卡曼滤波(ensemble Kalman filter)结合,实现了DWT条件下的反演[29]。Calderón等[34]发现,DCT比DWT更加符合压缩感知理论中的RIP条件,从而能够获得更优的反演结果。但是,另有研究发现,基于结构化压缩感知理论,DWT域参数的群稀疏结构与标准稀疏正则化相比具有更强的约束性,能够获得更加准确的反演结果[35-37]。此外,由于不适定反演无法考虑表示复杂结构的高频基向量,因此DCT和DWT均存在无法捕捉参数场复杂结构的问题。Khaninezhad等[38-39]通过字典学习(dictionary learning)构造地质字典,解决了这一问题;并用实例展示了基于稀疏字典的参数正则化方法在储层性质估计方面相比于TSVD参数化反演的优越性[40-41]。
2.1.4 压缩感知框架下的反演算法研究在反演算法方面,模型参数反演算法的研究主要包含:基于压缩感知本身进展的算法研究和与传统方法结合的研究。除结构化压缩感知外,学者们对加权压缩感知[42]、贝叶斯压缩感知[43-44]等理论在不同参数反演场景下的适用性展开了研究。加权压缩感知的思想在参数正则化方法提出时就被纳入反演过程,而直到最近Calderon等[45]的研究才发现其实质是对于反演过程中样本数量要求的降低。不确定性量化是参数反演研究的一个新趋势,通常在贝叶斯压缩感知框架下对先验信息和观测数据进行概率处理,进而获取反演结果及其统计分布[46]。Li和Jafarpour[47]通过假设变换域参数服从普拉斯分布,通过相关向量机(relevance vector machine)算法实现了压缩感知框架下的贝叶斯反演及不确定性量化[48],这种基于稀疏贝叶斯估计的思想促进了参数反演不确定性量化的进一步发展[49]。此外,压缩感知与传统反演方法的结合正在成为一个新的研究热点,压缩感知与EnKF的结合解决了传统的EnKF框架无法整合参数空间结构先验信息及无法恢复地质沟道结构的不足[50-51];地质字典与随机最大似然法结合形成了一种计算复杂度较低且量化不确定性的新方法[52]。
图 1总结了流体运动模型静态参数反演中的压缩感知反演框架,该框架是传统参数化方法与正则化方法的融合,主要包含参数化方法、反演算法等相互关联的研究内容。实践表明,该框架能有效提高反演速度和反演精度,其核心思想“稀疏重构”也为传统参数化和正则化反演方法提供了新的发展思路。
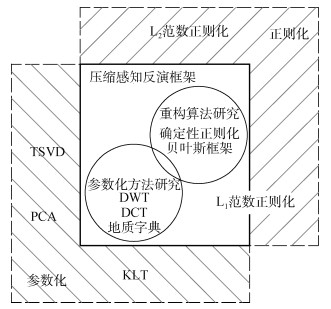
|
图 1 基于压缩感知的流体运动模型静态参数反演框架 Fig. 1 Inversion framework of static parameter in flow model based on compressive sensing |
土力学性质的空间分布和变化情况是岩土工程设计与分析的重要参数。在工程实践中,由于样本采集的局限性,通常将有限的样本数据与经验判断或统计假设相结合,对土力学性质的空间变化情况做出推断,这使得推断结果有着极大的不确定性。
在流体运动模型参数反演的基础上,压缩感知作为一种客观、合理的土力学性质空间数据重构方法被Wang和Zhao[53]引入岩土工程领域。尽管该方法在数据重构的过程中是完全客观的,但有限样本自身在统计上的不确定性无法消除,这会进一步传播并影响工程的设计和分析。因此,拥有不确定性量化能力的贝叶斯压缩感知在该领域得到了充分的研究。与石油工程、地质水文等领域针对参数化方法、重构算法展开的研究不同,压缩感知岩土工程领域的研究内容主要集中于不同维数的空间数据重构和模拟两个方面。
2.2.1 土力学性质的空间数据重构在空间数据重构方面,土力学性质随深度的变化(一维空间)是最基本的研究对象,可以将其看作根据测量分辨率和重构深度划分的一维信号。在DWT和DCT条件下,基于贝叶斯压缩感知的空间数据重构方法能够在有限数据的情况下重构出具有原始数据变化特征的平滑曲线,并且其重构精度高于普通克里格插值得到的数据[54-55]。此外,由贝叶斯压缩感知得到的统计不确定性量化指标——标准差,可以作为计算置信区间的基本参数,进而得到某个置信水平下的取值范围,为土力学性质的空间变化提供更加客观估计[56]。在一维空间的基础上,Zhao等[57-58]提出了基于贝叶斯压缩感知的二维和三维空间的地理数据重构方法,并在实例验证中取得了理想的效果;在高空间分辨率的情况下,地理数据表现出很强的空间相关性,能够有效保证基于压缩感知方法在不计算协方差或选取训练图像的条件下,较为准确地重构空间数据。此外,该方法无需假设空间数据是平稳的,从而使基于稀疏数据的垂直土壤分区得以实现[59]。
2.2.2 土力学性质的空间数据模拟土力学性质的空间数据模拟是在随机场理论的基础上展开的,基于压缩感知的空间数据模拟经历了由低维到高维、由简单到复杂的研究过程。在局部平均细分法[60]、协方差矩阵分解[61]、Karhunen–Loève (KL)展开[62]等诸多类型的随机场生成方法中,KL展开能够与贝叶斯压缩感知结合,形成一种更加高效的BCS-KL随机场生成方法。对于一维随机场,依靠贝叶斯压缩感知中表示不确定性的协方差矩阵,该方法可以跳过传统方法中的参数输入,由稀疏测量数据直接生成具有空间自相关性的随机场样本[63]。而又因为BCS-KL在生成随机场样本前未对样本数据进行去趋势处理,因此生成样本可以反映土力学性质真实的空间变化情况[64]。若使用贝叶斯压缩感知框架下的多任务压缩感知(multitask compressive sensing)替代其一般形式,则可以完成互相关随机场的模拟[65]。
在高维随机场的模拟中,基于贝叶斯压缩感知的“无参数”模拟方法表现出了更加明显的优越性。由BCS-KL改进得到的2D BCS-KL方法说明了这一点:在有限数据和空间结构参数未知的条件下,2D BCS-KL能够模拟出具有良好空间结构的样本,无论其原始分布是各向同性还是各向异性,而传统方法则需要通过大量样本数据取得相应的空间结构参数作为随机场的生成参数[66]。从模拟过程看,BCS-KL是在确定稀疏向量的解的基础上,根据解的不确定性进行的模拟;而与之相对应的则是直接获得不确定的解,根据不同的解重构出随机场样本,马尔科夫链蒙特卡洛(MCMC)模拟可以实现这一过程,这种方法在高维非静态、非高斯的随机场模拟中得到验证[67-68]。
目前,在岩土工程领域中已经形成了以贝叶斯压缩感知框架为核心的空间数据重构和模拟的双重体系(图 2)。基于该框架的重构和模拟方法在过程中无需估计相应的统计或空间结构参数,就能够从有限的空间样本中重构出与实际数据相近的空间结构。并且,这类方法不包含空间数据的平稳假设,因此其适用范围更广、实用性更强。
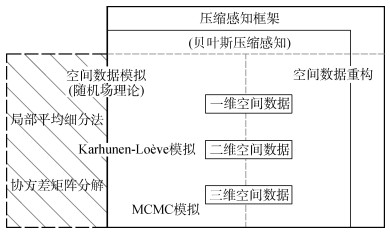
|
图 2 基于压缩感知的土力学性质空间数据重构及模拟框架 Fig. 2 Spatial data reconstruction and simulation framework of soil mechanical properties based on compressive sensing |
压缩感知起源于信号处理领域,近年来被引入诸多研究领域,逐渐形成各领域与信号处理领域交叉融合的新趋势。在地学领域中,已经形成了以压缩感知为核心的空间数据重构及模拟框架。该框架下,流体运动模型静态参数反演和土力学性质重构、模拟的效率及精度明显提升,对于稀疏样本的适应性明显增强。这主要依赖于压缩感知框架基于变换域的空间结构信息获取方式:具有空间相关性的空间域特征参数被投影至变换域后,其空间结构信息集中于少量变换域参数,这些参数信息隐藏于每个空间域样本中,当空间样本在变换域相互独立时,可以通过空间样本获取变换域参数,从而得到空间结构信息。这种方式为稀疏样本的空间数据重构提供了有效保证,与传统地统计学基于大量空间样本的空间域获取方式有着明显不同[69]。
土壤作为一种地质介质,其特性不仅包括土力学参数,也包括影响土壤治理措施制定和精准农业决策管理的污染物浓度、水盐含量以及养分状况等[70-72]。对于后者,目前常用的地统计学方法和机器学习方法以一定数量空间样本为基础建立数学模型,需要花费较高的成本进行数据采集[73-74]。基于压缩感知的空间数据重构框架为上述土壤特性的空间数据获取提供了新的思路。以较低的数据采集成本获取相对可靠的土壤特性空间分布数据,对土壤修复、改良及农业生产等实践活动具有重要意义。因此,需要从土壤学、环境科学等角度出发,对基于压缩感知的数据重构框架展开更加深入、全面的研究。结合该框架在地学领域的研究现状,本文提出以下几点潜在的研究方向:
1) 研究尺度、精度以及样本数量之间的关系。尺度和精度是空间数据研究中两个相互关联的重要因素,在某一尺度下,精度的划分决定未知参数的数量,未知参数估计的准确性与样本数量密切相关。若划分精度过高,则会因变换域参数数量的增加而无法完成准确估计;反之,则会因为空间域的子空间数量过少而忽略部分土壤特性的分布特征。因此,针对某一土壤特性,定量研究三者之间的关系,实行科学合理的精度划分,是土壤特性空间数据重构的重要基础。
2) 研究构建变换域参数约束的方法。小尺度、高精度是土力学性质研究对象的主要特点,该特点使测量数据能够充分代表某一子空间范围内的土力学性质以及变换域的空间结构信息。因此在重构过程中,只需将基向量搜索空间控制在低频区域,而无需施加额外约束。而污染物浓度、养分状况等土壤特性则不同,其研究尺度远大于土力学性质的研究尺度。大尺度下样本点无法充分代表子空间的土壤性质,这会削弱土壤特性空间相关性的表达,同时降低变换域参数估计的准确性。这一问题可以通过施加变换域参数的约束加以解决[53]。
3) 研究基于压缩感知的混合方法。从现有研究中可以发现,压缩感知作为空间数据重构方法并非完全独立。当它与多点地统计学[32]、径向基函数[75]等现有方法结合,能够发挥出良好的空间数据重构效果;而当它与随机场理论结合时,则成为一种灵活、有效的随机场生成工具[63]。因此,在进行关于土壤特性的相关研究时,探索现有插值方法与压缩感知的结合形式,或许是提高数据重构效果的有效手段。
4) 关于压缩感知本身的研究。变换矩阵与求解算法是压缩感知理论研究中的两个主要方面[76]。稀疏字典变换矩阵研究中的一个主要方向,目前基于K-SVD的“地质字典”被用于复杂地下特征的反演。而更加高效的字典生成方法则有待进一步探索。在面对复杂土壤特性分布时,使用更加高效的字典生成方法,构造“土壤字典”,对于提高稀疏表达效率和数据重构效果具有重要意义。此外,根据不同的数据重构目标,从不断优化的重构算法中筛选出适用的算法,也是一个值得探索的方向。
3 结语基于压缩感知的空间数据重构方法充分利用了地学特征的空间相关性,具有弱化样本采集规则以及控制结果随机性的双重优点,在流体运动模型的静态参数反演和土力学性质重构中得到了有效验证。对于不同的土壤特性,探索压缩感知在空间数据重构中的适用性,形成完整的理论体系,可以提高土壤修复、改良及农业生产等实践活动的数据采集效率,降低数据采集成本,为措施制定和相关决策提供坚实可靠的数据支撑。
| [1] |
土壤理化性质空间变异性研究进展[J]. 鲁东大学学报(自然科学版), 2016, 32(4): 372-378 DOI:10.3969/j.issn.1673-8020.2016.04.016 (  0) 0) |
| [2] |
空间变异理论及应用[M].
科学出版社, 北京, 2005
(  0) 0) |
| [3] |
地统计学在土壤空间变异研究中的应用[J]. 土壤通报, 2005, 36(2): 265-268 DOI:10.3321/j.issn:0564-3945.2005.02.029 (  0) 0) |
| [4] |
Emmanuel G, Deutsch C V. Teacher"s aide variogram interpretation and modeling[J]. Mathematical Geology, 2001, 33(4): 507-534 DOI:10.1023/A:1011093014141 (  0) 0) |
| [5] |
王海洋. 基于多点地质统计学的贝叶斯叠前反演方法研究[D]. 北京: 中国石油大学(北京), 2018.
(  0) 0) |
| [6] |
Jin L. A review of spatial interpolation methods for environmental scientists[J]. Record Geoscience Australia, 2008.
(  0) 0) |
| [7] |
Malone B P, Jha S K, Minasny B, et al. Comparing regression-based digital soil mapping and multiple-point geostatistics for the spatial extrapolation of soil data[J]. Geoderma, 2016, 262: 243-253 DOI:10.1016/j.geoderma.2015.08.037 (  0) 0) |
| [8] |
利用马尔科夫链模型对多点地质统计建模影响因素分析及优化[J]. 数学的实践与认识, 2016, 46(1): 202-211 (  0) 0) |
| [9] |
Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306 DOI:10.1109/TIT.2006.871582 (  0) 0) |
| [10] |
Candes E J, Romberg J, Tao T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509 DOI:10.1109/TIT.2005.862083 (  0) 0) |
| [11] |
Candès E J, Romberg J K, Tao T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure and Applied Mathematics, 2006, 59(8): 1207-1223 DOI:10.1002/cpa.20124 (  0) 0) |
| [12] |
Donoho D L. High-dimensional centrally symmetric polytopes with neighborliness proportional to dimension[J]. Discrete & Computational Geometry, 2006, 35(4): 617-652 (  0) 0) |
| [13] |
Rani M, Dhok S B, Deshmukh R B. A systematic review of compressive sensing: Concepts, implementations and applications[J]. IEEE Access, 2018, 6: 4875-4894 DOI:10.1109/ACCESS.2018.2793851 (  0) 0) |
| [14] |
Baraniuk R. A lecture on compressive sensing[J]. Signal Processing, 2007, 24(4): 1-9 DOI:10.1109/MSP.2007.4286554 (  0) 0) |
| [15] |
Candes E J, Wakin M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30 DOI:10.1109/MSP.2007.914731 (  0) 0) |
| [16] |
Baraniuk R, Davenport M, DeVore R, et al. A simple proof of the restricted isometry property for random matrices[J]. Constructive Approximation, 2008, 28(3): 253-263 DOI:10.1007/s00365-007-9003-x (  0) 0) |
| [17] |
压缩感知理论及其研究进展[J]. 电子学报, 2009, 37(5): 1070-1081 DOI:10.3321/j.issn:0372-2112.2009.05.028 (  0) 0) |
| [18] |
Candes E J, Tao T. Near-optimal signal recovery from random projections: Universal encoding strategies?[J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406-5425 DOI:10.1109/TIT.2006.885507 (  0) 0) |
| [19] |
Chen S S, Donoho D L, Saunders M A. Atomic decomposition by basis pursuit[J]. SIAM Review, 2001, 43(1): 129-159 DOI:10.1137/S003614450037906X (  0) 0) |
| [20] |
压缩感知回顾与展望[J]. 电子学报, 2011, 39(7): 1651-1662 (  0) 0) |
| [21] |
Pati Y C, Rezaiifar R, Krishnaprasad P S. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition[C]//Proceedings of 27th Asilomar Conference on Signals, Systems and Computers. November 1-3, 1993, Pacific Grove, CA, USA. IEEE, 1993: 40–44.
(  0) 0) |
| [22] |
Candès E, Romberg J. Sparsity and incoherence in compressive sampling[J]. Inverse Problems, 2007, 23(3): 969-985 DOI:10.1088/0266-5611/23/3/008 (  0) 0) |
| [23] |
Zhou H Y, Gómez-Hernández J J, Li L P. Inverse methods in hydrogeology: Evolution and recent trends[J]. Advances in Water Resources, 2014, 63: 22-37 DOI:10.1016/j.advwatres.2013.10.014 (  0) 0) |
| [24] |
Mishra P K, Kuhlman K L. Advances in Hydrogeology[M]. New York, NY: Springer New York, 2013.
(  0) 0) |
| [25] |
Jacquard P. Permeability distribution from field pressure data[J]. Society of Petroleum Engineers Journal, 1965, 5(4): 281-294 DOI:10.2118/1307-PA (  0) 0) |
| [26] |
Gavalas G R, Shah P C, Seinfeld J H. Reservoir history matching by Bayesian estimation[J]. Society of Petroleum Engineers Journal, 1976, 16(6): 337-350 DOI:10.2118/5740-PA (  0) 0) |
| [27] |
Reynolds A C, He N Q, Chu L F, et al. Reparameterization techniques for generating reservoir descriptions conditioned to variograms and well-test pressure data[J]. SPE Journal, 1996, 1(4): 413-426 DOI:10.2118/30588-PA (  0) 0) |
| [28] |
Lu P B, Horne R N. A multiresolution approach to reservoir parameter estimation using wavelet analysis[C]//All Days. October 1-4, 2000. Dallas, Texas. SPE, 2000.
(  0) 0) |
| [29] |
Jafarpour B. Wavelet reconstruction of geologic facies from nonlinear dynamic flow measurements[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(5): 1520-1535 DOI:10.1109/TGRS.2010.2089464 (  0) 0) |
| [30] |
Constable S C, Parker R L, Constable C G. Occam's inversion: A practical algorithm for generating smooth models from electromagnetic sounding data[J]. GEOPHYSICS, 1987, 52(3): 289-300 DOI:10.1190/1.1442303 (  0) 0) |
| [31] |
Yu M C, Dougherty D E. Modified total variation methods for three-dimensional electrical resistance tomography inverse problems[J]. Water Resources Research, 2000, 36(7): 1653-1664 DOI:10.1029/2000WR900072 (  0) 0) |
| [32] |
Jafarpour B, Goyal V K, McLaughlin D B, et al. Transform-domain sparsity regularization for inverse problems in geosciences[J]. GEOPHYSICS, 2009, 74(5): R69-R83 DOI:10.1190/1.3157250 (  0) 0) |
| [33] |
Jafarpour B, Goyal V K, McLaughlin D B, et al. Compressed history matching: Exploiting transform-domain sparsity for regularization ofNonlinear dynamic data integration problems[J]. Mathematical Geosciences, 2010, 42(1): 1-27 DOI:10.1007/s11004-009-9247-z (  0) 0) |
| [34] |
Calderón H, Silva J F, Ortiz J M, et al. Reconstruction of channelized geological facies based on RIPless compressed sensing[J]. Computers & Geosciences, 2015, 77: 54-65 (  0) 0) |
| [35] |
Duarte M F, Eldar Y C. Structured compressed sensing: From theory to applications[J]. IEEE Transactions on Signal Processing, 2011, 59(9): 4053-4085 DOI:10.1109/TSP.2011.2161982 (  0) 0) |
| [36] |
Bach F, Jenatton R, Mairal J, et al. Structured sparsity through convex optimization[J]. Statistical Science, 2012, 27(4): 450-468 (  0) 0) |
| [37] |
Golmohammadi A, Khaninezhad M R M, Jafarpour B. Group-sparsity regularization for ill-posed subsurface flow inverse problems[J]. Water Resources Research, 2015, 51(10): 8607-8626 DOI:10.1002/2014WR016430 (  0) 0) |
| [38] |
Khaninezhad M M, Jafarpour B, Li L L. Sparse geologic dictionaries for subsurface flow model calibration: Part Ⅰ. Inversion formulation[J]. Advances in Water Resources, 2012, 39: 106-121 DOI:10.1016/j.advwatres.2011.09.002 (  0) 0) |
| [39] |
Khaninezhad M M, Jafarpour B, Li L L. Sparse geologic dictionaries for subsurface flow model calibration: Part Ⅱ. Robustness to uncertainty[J]. Advances in Water Resources, 2012, 39: 122-136 DOI:10.1016/j.advwatres.2011.10.005 (  0) 0) |
| [40] |
Khaninezhad M R, Jafarpour B. Sparse geologic dictionaries for field-scale history matching application[C]//SPE Reservoir Simulation Symposium. Houston, Texas, USA. Society of Petroleum Engineers, 2015.
(  0) 0) |
| [41] |
Khaninezhad M R M, Jafarpour B. Field-scale history matching with sparse geologic dictionaries[J]. Journal of Petroleum Science and Engineering, 2018, 170: 967-991 DOI:10.1016/j.petrol.2018.06.024 (  0) 0) |
| [42] |
Candès E J, Wakin M B, Boyd S P. Enhancing sparsity by reweighted ℓ _1 minimization[J]. Journal of Fourier Analysis and Applications, 2008, 14(5/6): 877-905 (  0) 0) |
| [43] |
He L H, Carin L. Exploiting structure in wavelet-based Bayesian compressive sensing[J]. IEEE Transactions on Signal Processing, 2009, 57(9): 3488-3497 DOI:10.1109/TSP.2009.2022003 (  0) 0) |
| [44] |
Ji S H, Dunson D, Carin L. Multitask compressive sensing[J]. IEEE Transactions on Signal Processing, 2009, 57(1): 92-106 DOI:10.1109/TSP.2008.2005866 (  0) 0) |
| [45] |
Calderon H, Santibañez F, Silva J F, et al. Geological facies recovery based on weighted L1-regularization[J]. Mathematical Geosciences, 2020, 52(5): 593-617 DOI:10.1007/s11004-019-09825-5 (  0) 0) |
| [46] |
Ulrych T J, Sacchi M D, Woodbury A. A Bayes tour of inversion: A tutorial[J]. GEOPHYSICS, 2001, 66(1): 55-69 DOI:10.1190/1.1444923 (  0) 0) |
| [47] |
Li L L, Jafarpour B. A sparse Bayesian framework for conditioning uncertain geologic models to nonlinear flow measurements[J]. Advances in Water Resources, 2010, 33(9): 1024-1042 DOI:10.1016/j.advwatres.2010.06.005 (  0) 0) |
| [48] |
Tipping M. Sparse Bayesian learning and the relevance vector machine[J]. Journal of Machine Learning Research, 2001, 1: 211-244 (  0) 0) |
| [49] |
Lee J, Kitanidis P K. Bayesian inversion with total variation prior for discrete geologic structure identification[J]. Water Resources Research, 2013, 49(11): 7658-7669 DOI:10.1002/2012WR013431 (  0) 0) |
| [50] |
Sana F, Katterbauer K, Al-Naffouri T Y, et al. Orthogonal matching pursuit for enhanced recovery of sparse geological structures with the ensemble Kalman filter[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(4): 1710-1724 DOI:10.1109/JSTARS.2016.2518119 (  0) 0) |
| [51] |
Sana F, Katterbauer K, Al-Naffouri T, et al. Enhanced recovery of subsurface geological structures using compressed sensing and the Ensemble Kalman filter[C]//2015 IEEE International Geoscience and Remote Sensing Symposium. July 26-31, 2015, Milan, Italy. IEEE, 2015: 3107–3110.
(  0) 0) |
| [52] |
Khaninezhad M M, Jafarpour B. Sparse Randomized Maximum Likelihood (SpRML) for subsurface flow model calibration and uncertainty quantification[J]. Advances in Water Resources, 2014, 69: 23-37 DOI:10.1016/j.advwatres.2014.02.005 (  0) 0) |
| [53] |
Wang Y, Zhao T Y. Interpretation of soil property profile from limited measurement data: A compressive sampling perspective[J]. Canadian Geotechnical Journal, 2016, 53(9): 1547-1559 DOI:10.1139/cgj-2015-0545 (  0) 0) |
| [54] |
Wang Y, Zhao T. Statistical interpretation of soil property profiles from sparse data using Bayesian compressive sampling[J]. Géotechnique, 2017, 67(6): 523-536 DOI:10.1680/jgeot.16.P.143 (  0) 0) |
| [55] |
Wang Y, Akeju O V, Zhao T Y. Interpolation of spatially varying but sparsely measured geo-data: A comparative study[J]. Engineering Geology, 2017, 231: 200-217 DOI:10.1016/j.enggeo.2017.10.019 (  0) 0) |
| [56] |
Zhao T Y, Montoya-Noguera S, Phoon K K, et al. Interpolating spatially varying soil property values from sparse data for facilitating characteristic value selection[J]. Canadian Geotechnical Journal, 2018, 55(2): 171-181 DOI:10.1139/cgj-2017-0219 (  0) 0) |
| [57] |
Zhao T Y, Hu Y, Wang Y. Statistical interpretation of spatially varying 2D geo-data from sparse measurements using Bayesian compressive sampling[J]. Engineering Geology, 2018, 246: 162-175 DOI:10.1016/j.enggeo.2018.09.022 (  0) 0) |
| [58] |
Zhao T Y, Wang Y. Statistical interpolation of spatially varying but sparsely measured 3D geo-data using compressive sensing and variational Bayesian inference[J]. Mathematical Geosciences, 2021, 53(6): 1171-1199 DOI:10.1007/s11004-020-09913-x (  0) 0) |
| [59] |
Wang Y, Hu Y, Zhao T Y. Cone penetration test (CPT)-based subsurface soil classification and zonation in two-dimensional vertical cross section using Bayesian compressive sampling[J]. Canadian Geotechnical Journal, 2020, 57(7): 947-958 DOI:10.1139/cgj-2019-0131 (  0) 0) |
| [60] |
Fenton G A, Vanmarcke E H. Simulation of random fields via local average subdivision[J]. Journal of Engineering Mechanics, 1990, 116(8): 1733-1749 DOI:10.1061/(ASCE)0733-9399(1990)116:8(1733) (  0) 0) |
| [61] |
Zhu H, Zhang L M, Xiao T, et al. Generation of multivariate cross-correlated geotechnical random fields[J]. Computers and Geotechnics, 2017, 86: 95-107 DOI:10.1016/j.compgeo.2017.01.006 (  0) 0) |
| [62] |
Huang S P, Quek S T, Phoon K K. Convergence study of the truncated Karhunen–Loeve expansion for simulation of stochastic processes[J]. International Journal for Numerical Methods in Engineering, 2001, 52(9): 1029-1043 DOI:10.1002/nme.255 (  0) 0) |
| [63] |
Wang Y, Zhao T Y, Phoon K K. Direct simulation of random field samples from sparsely measured geotechnical data with consideration of uncertainty in interpretation[J]. Canadian Geotechnical Journal, 2018, 55(6): 862-880 DOI:10.1139/cgj-2017-0254 (  0) 0) |
| [64] |
Wang Y, Zhao T Y, Hu Y, et al. Simulation of random fields with trend from sparse measurements without detrending[J]. Journal of Engineering Mechanics, 2019, 145(2): 04018130 DOI:10.1061/(ASCE)EM.1943-7889.0001560 (  0) 0) |
| [65] |
Zhao T Y, Wang Y. Simulation of cross-correlated random field samples from sparse measurements using Bayesian compressive sensing[J]. Mechanical Systems and Signal Processing, 2018, 112: 384-400 DOI:10.1016/j.ymssp.2018.04.042 (  0) 0) |
| [66] |
Hu Y, Zhao T Y, Wang Y, et al. Direct simulation of two-dimensional isotropic or anisotropic random field from sparse measurement using Bayesian compressive sampling[J]. Stochastic Environmental Research and Risk Assessment, 2019, 33(8/9): 1477-1496 (  0) 0) |
| [67] |
Zhao T Y, Wang Y. Non-parametric simulation of non-stationary non-Gaussian 3D random field samples directly from sparse measurements using signal decomposition and Markov Chain Monte Carlo (MCMC) simulation[J]. Reliability Engineering & System Safety, 2020, 203: 107087 (  0) 0) |
| [68] |
Zhao T Y, Xu L, Wang Y. Fast non-parametric simulation of 2D multi-layer cone penetration test (CPT) data without pre-stratification using Markov Chain Monte Carlo simulation[J]. Engineering Geology, 2020, 273: 105670 DOI:10.1016/j.enggeo.2020.105670 (  0) 0) |
| [69] |
Heuvelink G B M, Webster R. Modelling soil variation: Past, present, and future[J]. Geoderma, 2001, 100(3/4): 269-301 (  0) 0) |
| [70] |
土壤水分空间变异性对灌溉决策的影响研究[J]. 干旱地区农业研究, 2000, 18(2): 80–85, 90 DOI:10.3321/j.issn:1000-7601.2000.02.014 (  0) 0) |
| [71] |
水网平原稻田土壤养分空间变异特性研究[J]. 中国水稻科学, 2005, 19(2): 153-159 DOI:10.3321/j.issn:1001-7216.2005.02.012 (  0) 0) |
| [72] |
Camilli A, Cugnasca C E, Saraiva A M, et al. From wireless sensors to field mapping: Anatomy of an application for precision agriculture[J]. Computers and Electronics in Agriculture, 2007, 58(1): 25-36 DOI:10.1016/j.compag.2007.01.019 (  0) 0) |
| [73] |
Heung B, Ho H C, Zhang J, et al. An overview and comparison of machine-learning techniques for classification purposes in digital soil mapping[J]. Geoderma, 2016, 265: 62-77 DOI:10.1016/j.geoderma.2015.11.014 (  0) 0) |
| [74] |
Morellos A, Pantazi X E, Moshou D, et al. Machine learning based prediction of soil total nitrogen, organic carbon and moisture content by using VIS-NIR spectroscopy[J]. Biosystems Engineering, 2016, 152: 104-116 DOI:10.1016/j.biosystemseng.2016.04.018 (  0) 0) |
| [75] |
Ryu, S. et al. Spatial Interpolation of Gauge Measured Rainfall Using Compressed Sensing. Asia-Pacific J. Atmos. Sci. 57, 331–345 (2021).
(  0) 0) |
| [76] |
Shi G M, Liu D H, Gao D H, et al. Advances in theory and application of compressed sensing[J]. Acta Electronica Sinica, 2009, 37(5): 1070-1081 (  0) 0) |
2. University of Chinese Academy of Sciences, Beijing 100049, China
 2022, Vol. 54
2022, Vol. 54


