传统获取土壤养分信息的化学分析法操作复杂、经济成本高、实时性差,且化学法所用到的试剂具有腐蚀性,不仅对人体有害,还污染环境[1]。而近红外光谱分析法根据物质在近红外波段的光谱特征来实时快速测量土壤养分信息,能够快速测绘田间养分全息图[2]。近年来,近红外光谱分析技术发展迅速,在土壤氮含量检测方面取得了广泛关注[3]。利用近红外光谱分析技术获取土壤成分信息具有检测速度快、操作简单、可原位检测、无环境污染等优点[4-5],已成为国内外学者研究的重点。
由于土壤是一种成分复杂的混合物,且光谱携带的信息量巨大,往往很难通过单个波长特征来预测土壤氮含量。国内外很多学者通过选用合适的特征提取算法来获取与土壤养分相关的特定光谱数据,以此建立敏感波长与土壤养分含量之间的映射关系,提高了土壤养分预测模型的精度。周鹏等[6]采用灰度关联法得到土壤全氮含量的敏感波长分别是1 007、1 128、1 360、1 596、1 696、1 836、2 149、2 262 nm。Wang等[7]研究表明,车载全氮含量预测系统在945、1 045、1 200、1 300、1 450、1 535和1 615 nm 7个敏感波长的近红外光谱反射率与土壤全氮含量高度相关。王昶等[8]使用偏最小二乘法(PLS)提取光谱数据中的特征波段及其线性组合来构建全氮含量预测模型,该模型对全碳、全氮和碳氮比的预测取得了非常好的效果。PLS方法是一种被广泛使用的线性回归方法,但是在自然界中,光谱与测量的土壤养分之间的关系很少是线性的。PLS模型不能充分反映光谱与相应土壤特性之间复杂的非线性关系。李燕等[9]采用神经网络构建多组分预测模型,成功地将人工神经网络应用在多组分定量测量领域。Xu等[10]基于中国余江地区稻田土壤的可见和近红外(Vis-NIR)光谱数据,发现反向传播(BP)神经网络模型能更好地解决土壤成分与光谱数据的非线性相关问题。但BP神经网络模型存在训练参数多,容易出现过拟合等问题。
近年来,基于卷积神经网络(CNN)的深度学习算法在图像数据处理方面取得了巨大进展。许多学者也将其适用范围扩展到了一维(1D)光谱数据。Padarian等[11]研究表明,CNN模型通过将土壤光谱数据作为输入预测含氮量,结果比传统的PLS回归模型表现更好。Ng等[12]基于凯洛格土壤调查实验室(KSSL)数据库构建了1D-CNN模型,并将其与2D-CNN模型进行比较,以估算土壤特性(全碳、有机碳、CEC、黏粒、砂粒和pH),结果表明1D-CNN模型比2D-CNN模型更有效。基于此,本研究应用1D-CNN模型基于近红外光谱数据对土壤全氮含量进行了预测,并比较了其与传统的PLS和BP神经网络模型的差异,以筛选预测土壤全氮含量的最优模型,为建立利用近红外光谱预测土壤全氮含量的模型提供科学依据,为实现土壤养分快速测定提供有效指导。
1 材料与方法 1.1 供试土壤供试土壤样本采自江苏省无锡市世外源果蔬种植基地内的玉米田。玉米田占地约139亩(1亩=667 m2),位于120°13'E,31°24'N,地势平坦、土壤肥力中等,土壤类型为褐土。
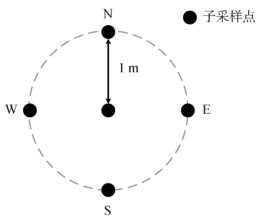
1.2 土壤样品采集与制备采样前,根据地形、土质等因素在田间均匀布点,每个采样点间隔15 ~ 20 m。采用LUCAS采样法[13](图 1)采集土样,每个采样点土样由5个子采样点土壤组成。采样时,首先去除土壤表面的枯枝败叶、垃圾和石子,再在每个子采样点处用铲子挖20 cm深的“V”字形缺口,取一侧约3 cm厚度的土壤去除其中的杂质后作为样本。每个子采样点采集100 g土壤,混合均匀后共计500 g土壤装入一个取样袋,作为该采样点的土样。在整个试验田共采集410个土样。土样采用避光包装,统一编号后装入塑封袋密封带回实验室。
|
图 1 LUCAS采样法 Fig. 1 LUCAS sampling method |
将土壤风干、研磨、过筛后进行化学检测和光谱检测。其中,化学检测使用半微量凯氏法检测土壤全氮含量,供试土壤全氮特征参数如表 1所示。光谱检测使用微型近红外光谱分析仪(NIR Quest 512型,海洋光学公司,英国)检测土壤样品的反射率。在对每个样品进行光谱测量前,使用标准反射板对光谱仪进行定标校准,之后记录3次光谱反射率的均值作为样品的原始光谱数据。该光谱的测量范围为900 ~ 2 500 nm,光谱采样间隔即波段宽为3.25 nm,由此得到534维的光谱数据。为了去除边缘波长区域(2 401 ~ 2 500 nm)的噪声影响,本研究使用900 ~ 2 040 nm的光谱带,所以每个样品保留350维数据。
|
|
表 1 供试土壤全氮含量的特征参数(n=410) Table 1 Statistical parameters of soil total nitrogen |
本研究对比了1D-CNN模型与PLS、BP神经网络模型的性能差别,并探究了不同光谱数据预处理方法对于模型性能的影响。所有模型均使用Python语言编写,选择Tensorflow作为后端的Keras深度学习框架,所有程序在配备119 GB RAM的NVIDIA Geforce GTX1080Ti显卡的128 GB RAM的Linux工作站(Ubuntu 20.04 LTS)上执行。
1.4.1 光谱数据预处理将原始光谱分别经过趋势校正(DT)、标准正态变换(SNV)、均值中心化(CT)处理,以比较不同预处理方法对模型性能的影响。其中,DT可以消除原光谱中的基线漂移[14],减少由不同采样部位、不同批次等因素对近红外光谱曲线带来的影响而放大由目标成分引起的光谱差异[15];SNV用来减小颗粒大小不均匀和粒子表面非特异性散射的影响[16];CT用于消除光谱数据之间量纲的影响,使不同数据之间具有可比性[17]。
1.4.2 PLS与BP神经网络模型构建本研究对PLS和BP神经网络模型参数做出了优化调整,以尽可能地提高两种传统模型的性能。经十折交叉验证将PLS模型的最优潜在变量数量确定为8;BP神经网络的学习率设为0.01,目标误差设为0.01,最大学习轮次设为100。
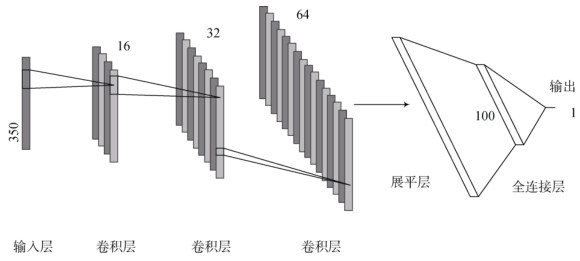
1.4.3 1D-CNN模型构建本研究提出了一个1D-CNN架构,如图 2所示,包括5个隐藏层(表 2):3个卷积层(convolutional layer)、1个展平层(flatten layer)、1个全连接层(fully-connected layer)。1D-CNN网络超参数如表 2所示。隐藏层第一层为卷积核大小为8×1的一维卷积层,该层在将通道数扩充到16的情况下感知较大尺度上的光谱特征;第二层为卷积核大小为4×1的一维卷积层,该层将通道数扩充到32并感知中等尺度上的光谱特征;第三层为卷积核大小为1×1的一维卷积层,该层再将通道数扩充2倍达到64通道,并感知最小尺度上的光谱特征;第四层将上一层的输出展平为一个向量,实现多维数据的一维化;第五层为全连接层,将上一层展平出的结果压缩为100×1的一维向量。整个网络除最后一层的激活函数为Linear外,其余层都使用ReLU作为激活函数。设置该网络模型训练时的学习率为0.1,学习轮次为100次。
|
图 2 1D-CNN网络结构图 Fig. 2 1D-CNN architecture |
|
|
表 2 1D-CNN网络超参数 Table 2 1D-CNN network hyperparameters |
本研究随机抽取90% 的光谱数据作为训练集,剩余10% 的光谱数据作为测试集。为了评估PLS、BP神经网络和1D-CNN模型的准确性,在训练数据集中进行了十折交叉验证。在这个过程中,训练数据被随机分成10份。每个模型建立在其中的9份数据上,然后将剩余的1份作为验证数据并计算误差;重复该过程,直到每一份数据都用作验证集。使用决定系数(R2)、均方根误差(RMSE)评估模型的准确性。RMSE用于衡量观测值与真实值之间的偏差,表示模型的稳定性,数值越小表示模型越稳定;R2用于评估预测值和真实值的符合程度,其值越接近1,说明模型和真实值符合程度越高。R2 > 0.90表明模型具有比较优秀的预测能力;0.82 < R2 < 0.90表明模型预测能力一般;0.65 < R2 < 0.82表明模型只能进行近似的粗略估计;R2 < 0.65则说明模型不能成功预测。
| $ {R^2} = 1 - \frac{{\sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} }}{{\sum\limits_{i = 1}^n {{{\left( {{y_i} - \bar y} \right)}^2}} }} $ | (1) |
| $ \text{RMSE} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^n {{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} $ | (2) |
式中:
表 3从R2和RMSE两个方面描述了在不同预处理方法下不同预测模型的性能表现。表中R2和RMSE为各模型在训练集上做十折交叉验证的结果。从表 3数据可以看出,本研究构建的1D-CNN模型在原始数据和经预处理的数据上表现出的性能均优于PLS和BP神经网络模型。在原始数据上,1D-CNN模型的R2值为0.907,明显高于PLS与BP神经网络模型的R2值(0.856和0.874);而1D-CNN模型的RMSE值为0.117,小于PLSR和BP神经网络模型的0.148和0.135,体现了1D-CNN模型在原始数据上拥有较强的泛化能力。
|
|
表 3 不同数据处理方式下的模型参数 Table 3 Model parameters under different processing methods |
基于3种预处理方法所构建的模型都有较高的精度。对于1D-CNN模型,数据预处理也为模型性能带来了显著提升,且比基于同样预处理方法的PLS和BP神经网络模型的表现更为优秀。此外,经过均值中心化、标准正态变换、趋势校正预处理后的数据构建的PLS模型的R2值分别为0.863、0.861、0.880,RMSE值也明显降低,说明数据预处理也给PLS带来了明显的性能提升。而对于BP神经网络模型,经过不同的预处理方法得到的R2都在0.900左右,说明数据预处理对BP神经网络模型性能的提升不如PLS模型。
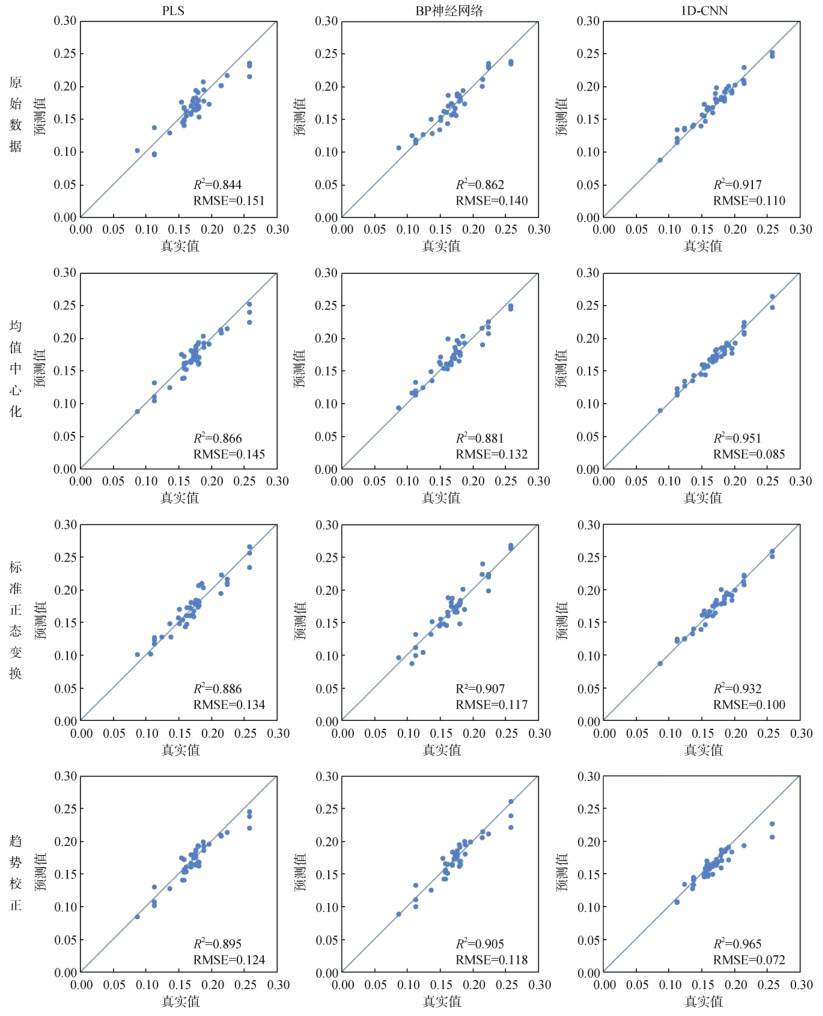
图 3是将测试集的光谱数据作为输入变量的3种预测模型经不同预处理方法得到的真实值与预测值的对比效果图。由图 3可以看出,1D-CNN模型预测土壤全氮含量的能力最好,被测点分布于1∶1线附近。此外,相对于PLS和BP神经网络模型,1D-CNN模型能够更好地拟合非常小的观察值(值接近于零),在全氮含量较低值处表现出了更好的预测能力。
|
图 3 不同数据处理方式下的模型回归效果图 Fig. 3 Model regression effects under different processing methods |
为了衡量1D-CNN模型准确性的增强能力,可以根据RMSE计算模型对土壤全氮含量预测的相对改进。在给定相同的光谱数据作为输入变量的情况下,与PLS模型相比,1D-CNN模型实现的相对精度提高范围为25.4% ~ 42.2%;与BP神经网络模型相比,1D-CNN模型实现的相对精度提高范围为14.5% ~ 39.2%。可见,本研究构建的1D-CNN模型网络结构相比于PLS和BP神经网络模型有明显的优势。Ng等[12]所构建的1D-CNN模型对KSSL土壤数据库中的土壤养分含量预测相较于PLS模型提高了41.8%,与本研究所建模型的估算结果一致。
本研究所构建的1D-CNN模型作为一种端对端的深度学习方法,无需预处理即可从原始光谱中自动提取线性和非线性特征,比传统方法具有更好的泛化性能[18]。在输入没有经过预处理的测试集中的原始光谱的情况下,得到的1D-CNN模型的R2值为0.917,表现出了较为优秀的预测能力,而传统的PLS模型和BP神经网络模型R2均未超过0.900。此外,高维和复杂的光谱数据不仅包含预期的目标信息,还包含大量冗余信息和无关噪声,会对模型的预测结果造成干扰,降低模型的准确性。通过对光谱数据进行预处理,可降低光谱中的噪声水平并消除斜率变化和基线偏移,从而提高光谱信号的分辨率和提高模型的准确性。在本研究中,经过均值中心化、标准正态变换和趋势校正3种预处理之后,PLS、BP神经网络和1D-CNN模型测试得到R2值均得到了提升,其中,趋势校正预处理方法对模型的改善效果最为明显,经趋势校正方法处理过的模型R2分别为0.880、0.911和0.964。
研究表明,通过稀疏连接和权重共享策略使得1D-CNN模型学习原始光谱局部抽象特征的能力出色。而与1D-CNN模型相比,PLS算法是提取光谱数据的潜在变量并构建具有最佳潜在变量数量的模型,潜在变量减少了原始光谱的维度,并捕获了土壤全氮含量和光谱之间的最大协方差[14]。但是提取最佳潜在变量而忽略其他次要特征变量会对模型的精度造成损失,而1D-CNN模型则可以将整个光谱数据全部纳入考虑,根据选用不同大小的卷积核来提取光谱不同尺度上的特征,其不仅能处理光谱特征与土壤全氮含量的线性映射关系,还能建立两者的非线性关系,从而达到比PLS模型更高的精度。
在Kuang等[19]的研究中,使用BP神经网络模型预测土壤有机碳、pH和黏土含量的效果都优于PLS模型;同样地,在本研究中BP神经网络模型在交叉验证和独立验证过程中的表现都优于PLS模型,预测误差均小于PLS模型,BP神经网络模型相比于PLS模型实现的相对精度提高范围为4.84% ~ 12.7%。相比于PLS模型,BP神经网络模型作为一种前馈神经网络,可以建立光谱特征与土壤全氮含量间的非线性映射关系,每个隐藏节点的信息可以使用激活函数将非线性变量传输到下一层,并通过对权重和偏差进行校正以减少测量值和真实值之间的误差。但是由于其各层以全连接的形式相连,所以易出现过拟合的问题,而1D-CNN模型可以通过添加池化层降低每个通道的特征维度来避免过拟合情况的出现,也因此可以将网络设计得比BP神经网络更深,从而提取出更多特征,达到比BP神经网络更好的效果。
4 结论本研究构建的1D-CNN模型在原始光谱数据上所训练的模型R2值为0.907,在原始光谱数据经均值中心化、标准正态变换、趋势校正处理后所训练得到的模型R2值分别为0.931、0.922和0.964。1D-CNN模型整体优于PLS和BP神经网络模型,并且在近红外光谱数据分辨率为3.25 nm的低分辨率情况下依然能够优于PLS与BP神经网络模型的性能。总之,1D-CNN模型能更好地提取光谱特征并建立其与含氮量的映射关系,在未经过预处理的光谱数据上依然能够达到一定的精度,可为实现对土壤养分的快速测定提供指导。
| [1] |
张娟娟, 熊淑萍, 时雷, 等. 基于近红外光谱分析的土壤全氮含量估测研究[J]. 土壤, 2015, 47(4): 653-657 (  0) 0) |
| [2] |
Zhang Z P, Ding J L, Zhu C M, et al. Strategies for the efficient estimation of soil organic matter in salt-affected soils through Vis-NIR spectroscopy: Optimal band combination algorithm and spectral degradation[J]. Geoderma, 2021, 382: 114729 DOI:10.1016/j.geoderma.2020.114729 (  0) 0) |
| [3] |
陈颂超, 冯来磊, 李硕, 等. 基于局部加权回归的土壤全氮含量可见-近红外光谱反演[J]. 土壤学报, 2015, 52(2): 312-320 (  0) 0) |
| [4] |
Viscarra Rossel R A, Cattle S R, Ortega A, et al. In situ measurements of soil colour, mineral composition and clay content by vis–NIR spectroscopy[J]. Geoderma, 2009, 150(3/4): 253-266 (  0) 0) |
| [5] |
马赵扬, 杜昌文, 周健民, 等. 黄土的红外反射光谱与红外光声光谱特征及其差异研究[J]. 土壤, 2012, 44(5): 862-867 DOI:10.3969/j.issn.0253-9829.2012.05.024 (  0) 0) |
| [6] |
周鹏, 杨玮, 李民赞, 等. 基于灰度关联-极限学习机的土壤全氮预测[J]. 农业机械学报, 2017, 48(S1): 271-276 DOI:10.6041/j.issn.1000-1298.2017.S0.041 (  0) 0) |
| [7] |
Wang W C, Yang W, Zhou P, et al. Development and performance test of a vehicle-mounted total nitrogen content prediction system based on the fusion of near-infrared spectroscopy and image information[J]. Computers and Electronics in Agriculture, 2022, 192: 106613 DOI:10.1016/j.compag.2021.106613 (  0) 0) |
| [8] |
王昶, 黄驰超, 余光辉, 等. 近红外光谱结合偏最小二乘法快速评估土壤质量[J]. 土壤学报, 2013, 50(5): 881-890 (  0) 0) |
| [9] |
李燕, 孙秀云, 王俊德. 人工神经网络法测定五组分红外光谱体系[J]. 光谱学与光谱分析, 2000, 20(6): 773-776 (  0) 0) |
| [10] |
Xu S X, Zhao Y C, Wang M Y, et al. Comparison of multivariate methods for estimating selected soil properties from intact soil cores of paddy fields by Vis-NIR spectroscopy[J]. Geoderma, 2018, 310: 29-43 DOI:10.1016/j.geoderma.2017.09.013 (  0) 0) |
| [11] |
Padarian J, Minasny B, McBratney A B. Using deep learning to predict soil properties from regional spectral data[J]. Geoderma Regional, 2019, 16: e00198 DOI:10.1016/j.geodrs.2018.e00198 (  0) 0) |
| [12] |
Ng W, Minasny B, Montazerolghaem M, et al. Convolutional neural network for simultaneous prediction of several soil properties using visible/near-infrared, mid-infrared, and their combined spectra[J]. Geoderma, 2019, 352: 251-267 DOI:10.1016/j.geoderma.2019.06.016 (  0) 0) |
| [13] |
Jones A, Fernandez-Ugalde O, Scarpa S. LUCAS 2015 Topsoil Survey. Presentation of dataset and results. JRC Technical Reports [R], EUR 30332 EN, 2020.
(  0) 0) |
| [14] |
Luypaert J, Heuerding S, Vander Heyden Y, et al. The effect of preprocessing methods in reducing interfering variability from near-infrared measurements of creams[J]. Journal of Pharmaceutical and Biomedical Analysis, 2004, 36(3): 495-503 DOI:10.1016/j.jpba.2004.06.023 (  0) 0) |
| [15] |
张进, 胡芸, 周罗雄, 等. 近红外光谱分析中的化学计量学算法研究新进展[J]. 分析测试学报, 2020, 39(10): 1196-1203 DOI:10.3969/j.issn.1004-4957.2020.10.003 (  0) 0) |
| [16] |
尼珍, 胡昌勤, 冯芳. 近红外光谱分析中光谱预处理方法的作用及其发展[J]. 药物分析杂志, 2008, 28(5): 824-829 (  0) 0) |
| [17] |
Buddenbaum H, Steffens M. The effects of spectral pretreatments on chemometric analyses of soil profiles using laboratory imaging spectroscopy[J]. Applied and Environmental Soil Science, 2012, 274903 (  0) 0) |
| [18] |
Haghi R K, Pérez-Fernández E, Robertson A H J. Prediction of various soil properties for a national spatial dataset of Scottish soils based on four different chemometric approaches: A comparison of near infrared and mid-infrared spectroscopy[J]. Geoderma, 2021, 396: 115071 DOI:10.1016/j.geoderma.2021.115071 (  0) 0) |
| [19] |
Kuang B Y, Tekin Y, Mouazen A M. Comparison between artificial neural network and partial least squares for on-line visible and near infrared spectroscopy measurement of soil organic carbon, pH and clay content[J]. Soil and Tillage Research, 2015, 146: 243-252 DOI:10.1016/j.still.2014.11.002 (  0) 0) |
 2023, Vol. 55
2023, Vol. 55

