土壤盐渍化是指可溶性盐在土壤表层的集聚现象,是农业发展、生态稳定和土壤资源可持续利用的主要限制因素[1]。全球广泛且不断扩张的盐渍土使盐渍化成为当前备受关注的环境和资源问题[2-4]。黄河三角洲作为典型的盐渍化滨海区,由于长期的海水渗透以及相对干旱的气候条件,盐渍化问题日益显著。此外,人类活动如不合理的土地利用和重灌轻排的耕作方式造成严重的次生盐渍化[5],使盐渍化问题更加复杂,造成农业生产力下降、生物多样性锐减、生态环境恶化等问题[3]。
掌握土壤含盐量(Soil salinity content,SSC)的空间分布特征可为盐渍土改良治理工作提供重要依据。传统地统计模型中的普通克里格(Ordinary kriging,OK)是最常用的SSC插值方法。OK通过各样本点之间SSC的空间依赖关系,在未知点提供最优线性无偏估计[6]。然而,SSC由于受多种环境因素的影响而具有高空间变异特征,难以满足传统地统计学要求的数据平稳性假设,因此,SSC样本的规模和特征较大地影响着地统计模型的应用[6-7]。受样本数据影响较小的线性回归模型可以有效地利用环境影响因素来反演SSC的空间分布,是近年来颇受欢迎的SSC插值方法。地理加权回归(Geographically weighted regression,GWR)模型利用空间变化的环境协变量系数捕捉样本数据的空间非平稳性[8-9],在最优带宽范围内建立局部线性方程对SSC进行预测。然而,线性回归建模受环境协变量与SSC之间的相关性的影响较大,导致模型的不稳定性。
贝叶斯最大熵(Bayesian maximum entropy,BME)是Christakos等[10]和He等[11-12]于20世纪90年代提出的一套灵活而严谨的非线性时空估计理论框架。与OK插值相比,其可以充分利用硬数据和软数据进行空间分析与估计,且不需要传统地统计学高斯分布和二阶平稳假设等前提条件。近年来,BME模型被广泛地应用于土壤属性的空间预测。高风杰等[13]将我国东北黑土丘陵区海沟河小流域表层有机质作为硬数据,不同土地类型作为软数据,通过BME模型预测有机质的空间分布,并与协同克里格方法进行对比,精度评价表明BME模型的整体预测精度高于协同克里格方法。刘欢瑶等[14]将亚热带红壤丘陵区有机碳密度作为硬数据,借助GWR模型结合地形、土地利用等多源数据获取软数据,应用BME结合GWR的耦合模型对土壤有机碳密度进行空间预测,得出耦合模型的预测精度高于GWR模型。Zhang等[15]将土壤有机质作为硬数据,将多元线性回归和GWR模型构造的95% 置信区间作为软数据,通过BME模型对湖北省沙洋县的有机质进行空间预测,得出相较于地统计学方法和线性回归模型,BME模型具有更低的预测误差和预测不确定性。Douaik等[16]利用BME模型结合区间软数据对霍尔多巴吉地区的SSC进行预测制图,得出BME模型的制图精度高于地统计模型。总之,国内外研究结果均表明,BME模型对土壤成分的空间预测精度要明显高于经典的地统计学方法和线性回归模型,但目前针对SSC方面的研究并不多见。
此前已有众多学者针对黄河三角洲盐渍土的空间分布展开了深入细致的研究,研究方法以经典的地统计方法和GWR方法为主,基于BME模型的SSC空间预测分析在当地尚未见报道。本研究以黄河三角洲SSC为研究对象,以高程、Landsat 9波段指数及距海距离等作为协变量构造区间型软数据,进而建立BME模型对SSC的空间分布进行预测,最后对不同方法SSC空间分布预测结果进行对比,以验证BME方法的有效性。
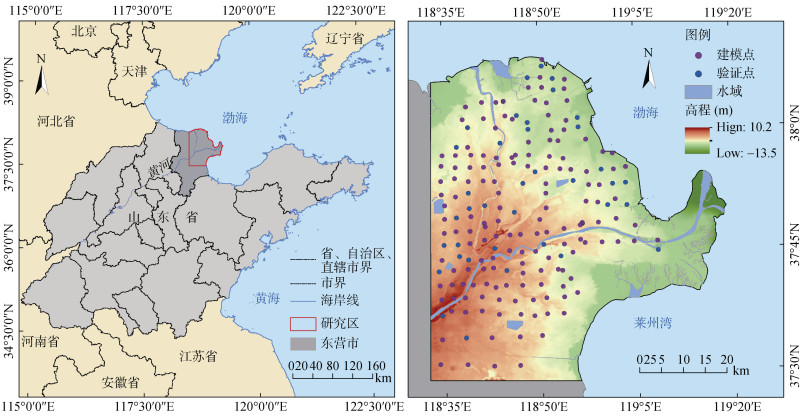
1 材料与方法 1.1 研究区概况研究区位于山东省东营市(图 1)黄河入海口地区,东临渤海和莱州湾,地处37°25′N ~ 38°10′N,118°30′E ~ 119°20′ E,面积约3 309 km2。该区域地形平坦,地势由西南向东北倾斜,高程在–13.5 ~ 10.2 m,区域内地下水埋深浅,易受海水的侵蚀,地下水矿化度高[17-18]。气候类型为暖温带半湿润大陆性季风气候,年降雨的74% 集中在6—9月[1],多年平均降水量约为560 mm[18],多年平均蒸发量约为1 962 mm,蒸降比约为3.5∶1。土壤类型以轻沙壤为主,毛细管作用强烈。在海水侵蚀和季节性干旱的气候条件下,区域内原生盐渍土广泛分布。此外,由于当地对土地资源的不合理开发利用,以及重灌轻排的耕作方式,导致土地次生盐渍化和生态恶化等问题频发。
|
图 1 研究区位置及采样点分布图 Fig. 1 Location of the study area and distribution of sampling points |
本研究采用的土壤调查数据来自均匀布置在黄河三角洲的193个土壤采样点(图 1),每个采样点包括表层(0 ~ 30 cm)与底层(90 ~ 100 cm)两个深度的SSC数据。采样点的间距约为3 km,采样时间为2022年5月23日至6月6日,在雨季来临之前。本研究对两个土层深度的SSC进行研究,分析区域内土壤盐渍化的垂直剖面特征,可为准确掌握黄河三角洲土壤盐渍化特征及其发展趋势提供可靠的数据支撑。在采样过程中使用取土器采集土样并进行封装标记,利用GPS记录采样点的经纬度,后将采样点投影到横轴墨卡托投影的坐标系下。将土样带回实验室后进行自然风干,剔除植被根系与砂石,然后研磨过0.5 mm孔筛,按照5∶1(V∶m)的水土比浸提土壤,SSC采用烘干称重法测定,pH采用pH计测定。根据3σ原则将平均值±3σ之外的SSC值视为异常值,并将异常值修改为正常最大或最小值,以避免异常值对插值结果的影响[19]。
1.3 环境协变量数据获取及预处理 1.3.1 遥感数据及其他数据的获取本研究使用的2022年5月15日的Landsat 9 OLI2遥感影像来自美国地质勘探局(https://earthexplorer.usgs.gov/),其成像时间与土壤采样时间接近,空间分辨率为30 m。利用ENVI软件对影像进行了辐射定标、大气矫正、几何矫正和裁剪等处理。DEM(Digital elevation model)数据为根据1∶10 000地形图等高线数字化后,在ArcGIS中生成,分辨率为10 m。
1.3.2 环境协变量的提取大量基于遥感影像的SSC反演研究表明,遥感影像的红光和近红外波段对土壤中的盐分较为敏感[20],且根据这些敏感波段计算出的植被指数、盐度指数和组合波段指数能有效地反映SSC的空间分布[21-22]。此外,SSC的空间格局还受外界环境和人类活动的直接影响。因此,本研究在前人研究成果的基础上选取了13个环境协变量,包括高程、距海距离(Distance to the sea,DTS)、pH、单波段(近红外(Near infrared,NIR)和短波红外(Shortwave infrared,SWIR1))、组合波段(Combined band,C2)、植被指数(归一化植被指数(Normalized difference vegetation index,NDVI)、差值植被指数(Difference vegetation index,DVI)、绿度归一化植被指数(Green normalized difference vegetation index,GNDVI)和改进土壤调节植被指数(Modified soil adjusted vegetation index,MSAVI))和盐度指数(Salinity Index,SI3、SI9、SI-T)。环境协变量的定义如表 1所示。
|
|
表 1 环境协变量及其定义 Table 1 Environmental covariates and their definitions |
1) 贝叶斯理论基础。时空随机场模型是BME的理论基础,该模型将自然过程抽象成具有空间和时间两个参数的随机变量的集合。p是空间s和时间t定义的点,即p=(s, t)。时空随机场X(p) 的期望值mx=E(X(p)) 表示时空随机场的整体趋势和时空结构性,协方差cx(p, p′) 表示任意两点之间的时空相关性[10]。
BME将所有的信息和数据分为两类,即广义知识和特定知识。广义知识主要包括协方差函数、物理法则、经验关系等;特定知识包括硬数据和软数据。BME方法有两个重要的步骤:①使用广义知识,基于最大熵原理,计算研究区内未测点变量分布的先验概率密度函数(probability density function, pdf),最大熵原理即在约束条件下,使一个系统的信息熵最大,引入拉格朗日乘数μα,得到先验pdf公式如下:
| $ {f_\text{G}}({Z_{{\text{map}}}}) = \frac{1}{A}\exp \left( {\sum\limits_{\alpha = 1}^{{N_c}} {{\mu _\alpha }{g_\alpha }({Z_{{\text{map}}}})} } \right) $ | (1) |
式中:fG(Zmap)表示先验pdf;Zmap=(Zhard,Zsoft,Z0),Zhard、Zsoft、Z0分别表示硬数据点、软数据点和估计点;gα是关于Zmap的已知函数;Nc为条件总数;A为归一化约束。
| $ A = \int {\exp \left( {\sum\limits_{\alpha = 1}^{{N_c}} {{\mu _\alpha }{g_\alpha }({Z_{{\text{map}}}})} } \right){\text{d}}{Z_{{\text{map}}}}} $ | (2) |
② 使用特定知识,基于贝叶斯条件概率公式,更新上一步得到的先验pdf,得到研究区内预测点变量分布的后验pdf:
| $ \begin{array}{l}{f}_{k}({Z}_{0})={f}_{\text{G}}({Z}_{0}|{Z}_{\text{hard}}\text{,}{Z}_{\text{soft}})\\ =\frac{{\displaystyle {\int }_{I}^{u}{f}_{\text{G}}({Z}_{0}\text{,}{Z}_{\text{hard}}\text{,}{Z}_{\text{soft}})\text{d}{Z}_{\text{soft}}}}{{\displaystyle {\int }_{I}^{u}{f}_{\text{G}}({Z}_{\text{hard}}\text{,}{Z}_{\text{soft}})\text{d}{Z}_{\text{soft}}}}\end{array} $ | (3) |
式中:fk(Z0)表示后验pdf;l和u分别为置信区间的下界和上界。根据后验pdf,利用预测均值进行SSC制图,预测均值定义如下:
| $ {\hat X_{{\text{mean}}}}({Z_0}) = \int {{Z_0}{f_k}({Z_0}){\text{d}}{Z_0}} $ | (4) |
式中:
2) 软数据构造。本研究将BME协方差分析得到的协方差函数和正规化约束作为广义知识,硬数据和构造的软数据作为特定知识。本文的硬数据是指采样点获取的土样经化验分析得到的SSC数据,软数据则是根据GWR模型的结果在研究区内1 200 m分辨率下2 271个空间格网点上计算得到的95% 置信区间。以表层SSC软数据构造为例,公式如下[15]:
| $ {\text{GI}}_{\text{GWR}}^{1-\alpha }({S}_\text{k})=\left[\begin{array}{l}{\overline{X}}_{\text{GWR}}-\frac{{S}_{\text{GWR}}}{\sqrt{\text{NL}}}{t}_{(\alpha /2)}(\text{NL}-1)\text{,}\\ {\overline{X}}_{\text{GWR}}+\frac{{S}_{\text{GWR}}}{\sqrt{\text{NL}}}{t}_{\alpha /2}(\text{NL}-1)\end{array}\right] $ | (5) |
式中:
1) OK法。OK法是目前应用最广泛的空间预测方法,其根据半变异或半方差函数确定各样本点对预测点的影响权重,在满足平稳假设、高斯假设等前提条件下,对研究对象进行最优线性无偏估计[23]。
2) GWR模型。GWR模型利用环境协变量对带宽范围内的样本点进行局部线性拟合,并且利用空间变化的协变量系数捕捉SSC的空间非平稳性。在GWR中,用高斯核函数表征SSC随样本点距离增加而衰减的形式,本文选用自适应带宽函数作为核函数,利用校正的Akaike信息标准法(AICc)确定带宽参数。GWR估计公式如下:
| $ {y_{{\text{GWR}}(u)}} = {\beta _{0(u)}} + \sum\limits_{i = 1}^n {{\beta _{i(u)}}{X_{i(u)}} + {\varepsilon _{(u)}}} $ | (6) |
式中:yGWR(u)为模型在位置u处的预测值;β0(u)为截距;βi(u)为i协变量在位置u的回归系数;Xi(u)为位置u处i协变量的值;n为协变量的个数;ε(u)为预测误差。本文利用安装在ArcGIS 10.2中的GTWR插件进行GWR建模。
1.4.3 模型精度评价本研究将土壤采样点SSC数据集划分为建模集(约占80%)和验证集(约占20%),选用平均绝对误差(Mean absolute error,MAE)、均方根误差(Root mean square error,RMSE)和决定系数(R2)来验证各模型对SSC的估算精度,并对比模型的效果。MAE和RMSE越低、R2越高表示模型预测精度越高,反之越低。具体公式如下:
| $ {\text{MAE}} = \frac{1}{n}\sum\limits_{i = 1}^n {(\left| {{o_i} - {p_i}} \right|)} $ | (7) |
| $ {\text{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{({o_i} - {p_i})}^2}} } $ | (8) |
| $ {R^2} = {\left[ {\frac{{\sum\limits_{i = 1}^n {({o_i} - \bar o)({p_i} - \bar p)} }}{{\sqrt {\sum\limits_{i = 1}^n {{{({o_i} - \bar o)}^2}} {{\sum\limits_{i = 1}^n {({p_i} - \bar p)} }^2}} }}} \right]^2} $ | (9) |
式中:oi为实测值;pi为预测值;
研究区采样点SSC统计特征见表 2所示。表层SSC在0.458 g/kg ~ 54.976 g/kg,平均值为8.628 g/kg,变异系数为152%,属强空间变异(< 10% 为弱变异,10% ~ 100% 为中等变异,> 100% 为强变异)。底层SSC在0.459 g/kg ~ 26.599 g/kg,平均值为4.516 g/kg,变异系数为120%,属强空间变异,平均值和变异系数较表层分别降低48% 和21%。可见,研究区SSC普遍较高,具有高空间变异特征,底层土盐渍化相对较轻,土壤盐分表聚现象明显。
|
|
表 2 采样点土壤含盐量的描述性统计特征 Table 2 Descriptive statistics of soil salinity contents in surface and bottom layers at sampling points |
表土盐渍化主要由底土和地下水中盐分的迁移和积累造成[3],因此,底层和表层SSC的空间格局存在一定的联系。本文将表层SSC预测结果作为一个底层SSC的预测因子,以提高底层SSC的空间预测精度[3, 24]。由表 3中SSC与环境协变量的相关性可知,底层SSC和表层SSC空间分布具有较高的正相关关系,此外,除SI-T与SSC呈现正相关外,其他协变量与SSC均呈现显著负相关。大部分环境协变量与SSC在P < 0.01水平上显著相关,但相关系数偏低(相关系数绝对值大部分在0.3 ~ 0.7)。基于遥感光谱的植被和盐度指数(如NDVI、DVI、GNDVI、MSAVI、SI-T)的相关性在土壤底层有所降低,这与遥感影像对深层SSC的敏感性降低有关[2-3]。
|
|
表 3 不同土层土壤含盐量与环境协变量相关性 Table 3 Correlations between soil salinity content and covariates at different soil layers |
本研究将显著性水平P < 0.05和方差膨胀因子VIF < 7.5作为筛选一组环境协变量的标准,最终在土壤表层筛选12组协变量建立12个GWR模型,在土壤底层筛选4组协变量建立4个GWR模型,基于表层12个和底层4个GWR模型的结果按式(5)构造出95% 置信区间,分别作为表层和底层SSC软数据。
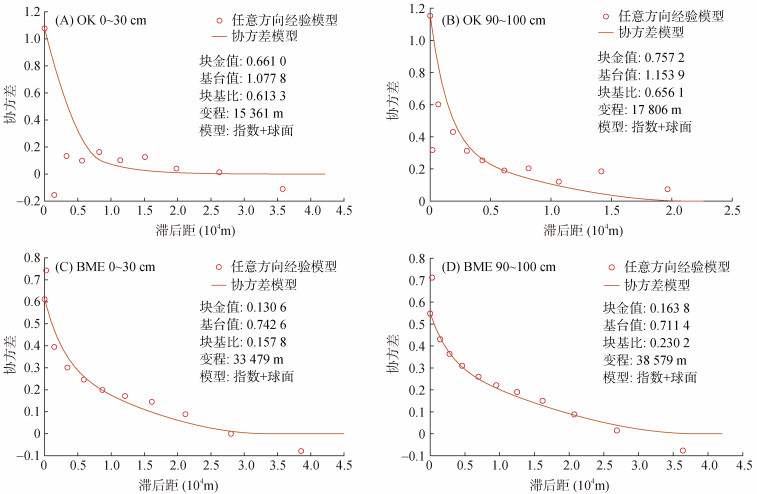
2.3 不同方法的半变异函数模型为了方便对比,本研究借助安装在MATLAB中的SEKS-GUI v0.69软件包完成OK和BME模型的协方差分析,相关协方差模型参数见图 2。块基比(C0/ (C0+C))表示随机变异与系统总变异的比值,该比值< 0.25表示高空间相关性,0.25 ~ 0.75表示中等强度空间相关性,> 0.75表示弱空间相关性。不同深度OK模型的块基比在0.61 ~ 0.66,属中等强度空间相关,而BME模型的块基比均 < 0.25,属高空间相关,说明软数据的加入增强了SSC样本之间的空间相关性。图中圆圈表示经验模型,曲线表示协方差模型,两者拟合度越高表明协方差模型越好。图 2C、2D中BME的协方差模型与经验模型的拟合度明显高于OK模型(图 2A、2B),说明BME模型的可靠性更高。
|
图 2 不同深度OK和BME的协方差模型参数 Fig. 2 Covariance model parameters of OK and BME models for different soil layers |
基于验证样本计算的各模型精度如表 4所示。综合各精度评价指标来看,不同深度SSC的GWR和BME模型的预测精度较OK模型均有显著提高,其中BME模型的预测精度最高。对于表层土壤,BME和GWR模型对SSC估算的RMSE与OK模型相比分别降低了25% 和14%,R2从0.069 7分别提高到0.612 9和0.305 1。对于底层土壤,BME和GWR模型对SSC估算的RMSE与OK模型相比分别降低了21% 和18%,R2从0.343 2分别提高到0.695 9和0.537 4。表明BME模型预测值与实测值的拟合程度显著高于其他方法。证明利用BME方法,结合与SSC显著相关的辅助变量,能有效地提高SSC的空间预测精度,较好地反映SSC的空间变异特征。
|
|
表 4 模型精度评价 Table 4 Accuracy assessment of different models |
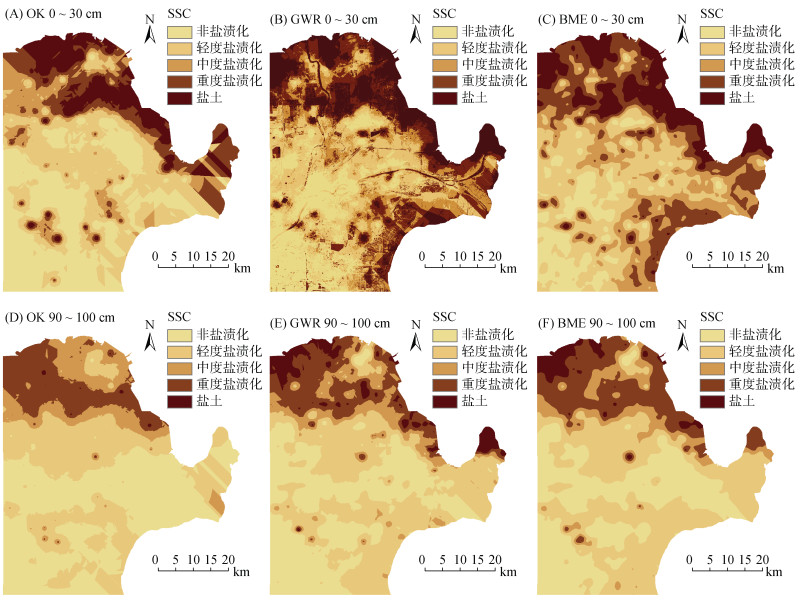
根据中国半湿润环境气候区SSC分级标准将盐渍化分为5个等级[25]:非盐渍化(0 ~ 2.0 g/kg)、轻度盐渍化(2.0 ~ 4.0 g/kg)、中度盐渍化(4.0 ~ 6.0 g/kg)、重度盐渍化(6.0 ~ 10.0 g/kg)和盐土(> 10.0 g/kg)。对3种模型得到的SSC空间分布进行分级,得到SSC空间分布如图 3所示。不同方法预测的SSC空间分布特征基本一致,即沿海地区大于内陆地区,东北地区大于西南地区,黄河沿岸SSC较低但存在多个局部土壤盐渍化区域,北部的老黄河入海口SSC明显大于现黄河入海口,大体呈现由西南向东北递增的趋势。基于OK模型预测的SSC平滑连续(图 3A、3D),盐渍土沿带状连续分布,但反映不出SSC分布差异的细节;基于GWR模型的预测图中(图 3B、3E),存在界限分明且SSC较高的条块状区域,这是由于各辅助变量来自遥感图像数据,SSC分布图受遥感光谱特征的影响,与自然条件下土壤盐分连续渐变的特征不符。基于BME方法的预测图(图 3C、3F)克服了OK插值的平滑效应,同时又结合了基于GWR模型构造的区间型软数据,得到的SSC空间分布特点更为合理,能够较为准确地反映黄河三角洲SSC的空间分布。
|
图 3 不同深度不同模型土壤含盐量的空间分布 Fig. 3 Spatial distribution of soil salinity content of different models at different soil layers |
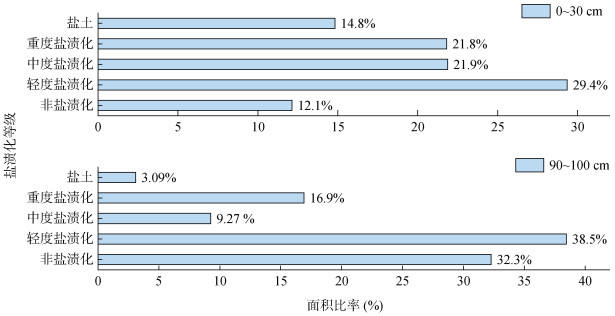
根据BME插值结果对研究区不同等级盐渍土面积进行统计,结果见图 4。结合图 3和4可知,黄河三角洲表层土壤约有88% 为不同程度的盐渍化土壤,其中重度盐渍化及以上的盐渍土约占37%,主要分布在北部黄河故道和孤北水库一带,以及东北沿渤海湾和东南沿莱州湾的滨海区域,在内陆也有一些零散分布。黄河沿岸两边的灌区由于排灌条件好,加上多年的人工改造和耕作历史,表层SSC相对较低。底层土壤中盐渍化土壤的面积占比约为68%,并且以轻度盐渍化土壤为主(约占38.5%)。底层土壤中的重度盐渍化及以上的土壤主要分布在黄河三角洲北部,而东南部莱州湾的盐渍化程度较低。可见,黄河三角洲北部的盐渍土属于上下均匀型,而南部的盐渍土属于盐分表聚型。
|
图 4 不同土层不同类型盐渍土面积统计 Fig. 4 Area statistics of soils under different degrees of salinization at different soil layers |
本研究选用了13个环境协变量包括基于遥感光谱的指数、高程、距海距离和pH等指标进行GWR建模及软数据构造。相关研究表明,遥感影像的SSC敏感波段(红外和近红外波段)以及基于这些敏感波段计算的植被和盐度指数可用于SSC的快速空间反演[20-22],但影像中不同地物之间的光谱连续特征导致较大的预测偏差,造成GWR模型得出了非真实的SSC空间分布的问题。此外,遥感影像只记录了表土信息,导致遥感指数与底层SSC的相关性较表层有所降低,以预测精度较高的表层SSC空间分布作为中间变量可以提高其他土壤深度SSC的空间分布预测精度[3, 24]。Li等[3]以表层土壤盐度为中间变量,提高了多深度土壤盐度的预测精度,弥补了遥感光谱对深层盐度不敏感的缺陷;Taghizadeh-Mehrjardi等[24]以两个深度实测盐度为中间变量,结合环境协变量对其他深度盐度进行预测,与不加盐度中间变量相比,预测精度有明显提高。基于地形的环境协变量如高程、坡向、坡度和地表粗糙度等是反映土壤盐分运移规律的有效指标[2, 26],由于黄河三角洲地势平缓,地形比降在1/8 000 ~ 1/12 000,因此,除高程以外,地形因子中的其他指标与SSC的相关关系并不显著。水的运动控制着盐分的运移、集聚和分布,距海距离是表征盐分来源的重要指标,与SSC存在显著的相关关系,在滨海低地区域,地下水埋深浅,矿化度高,盐分表聚现象明显,盐渍化问题突出[27]。
3.2 贝叶斯最大熵模型预测效果根据本研究中各模型的精度评价结果,BME模型对SSC的预测精度有显著的提升,但与相关研究相比其R2仍然较低。主要原因如下:①提取的环境协变量与SSC的相关性偏低。环境协变量与SSC的相关性影响软数据的质量,进而对BME的预测精度产生影响[15],导致BME模型的拟合优度偏低。相关SSC预测研究表明,协变量与SSC的相关系数一般不超过0.7,这在一定程度上限制了模型预测精度的提高。Li等[3]利用Landsat遥感波段数据提取的植被和盐度指数与SSC的相关性在0.5左右;吴春生等[5]提取了与SSC相关系数绝对值分别为0.379、0.499和0.045的高程、NDVI和河流距离作为协变量,导致建立的GWR模型的拟合优度偏低;Peng等[21]提取了大量遥感指数和地形指数作为协变量,这些指数与盐度的相关系数绝对值均小于0.65。此外,BME可以接受多种形式的软数据,软数据的获取不应局限于单一数据源,利用历史实测盐度数据、土壤电导率和地下水电导率等构造软数据也可能使BME达到理想的预测效果。②研究区和研究对象的特殊性。由于受河流、海洋、气候和人类活动等的影响,黄河三角洲土壤盐渍化具有明显的空间和季节变化特征,此外,受地表景观破碎化等因素的影响,其SSC具高度变异性和非连续性的特点。吴春生等[5]将高程、NDVI和河流距离作为协变量,应用GWR模型对黄河三角洲SSC进行空间预测,得到GWR模型的R2为0.421,在本研究GWR模型的R2(0.3 ~ 0.54)范围内,说明环境协变量的线性回归对SSC的解释度较低,黄河三角洲SSC具有特殊性。
4 结论1) SSC和环境协变量的相关性分析结果表明,大部分提取的环境协变量与SSC在P < 0.01水平上显著相关,但相关系数普遍偏低。除盐度指数SI-T与SSC呈显著正相关外,其他环境协变量与SSC均呈显著负相关。基于遥感光谱的植被和盐度指数与SSC的相关性随着土层深度的增加而有所降低。
2) 综合各精度评价指标,GWR和BME模型的预测精度较OK模型均有显著提高,其中BME模型是最佳SSC预测模型。对于土壤表层,BME模型对SSC估算的RMSE与OK和GWR模型相比分别降低了25% 和13%,R2分别从0.069 7和0.305 1提高到0.612 9。对于底层土壤,BME模型对SSC估算的RMSE与OK和GWR模型相比分别降低了21% 和4.2%,R2分别从0.343 2和0.537 4提高到0.695 9。从SSC空间分布看,BME模型充分展现了多源数据整合以及非线性估计的优势,能较好地反映SSC的空间变异特征,提高空间预测精度,较准确地反映了黄河三角洲SSC的空间分布特点。
3) 黄河三角洲土壤普遍存在盐渍化现象,SSC总体呈现由西南向东北递增的趋势。土壤表层重度盐渍化及以上的盐渍土约占37%,主要分布在东北沿渤海湾和东南沿莱州湾区域,以及一些内陆零散区域,空间变异特征明显。土壤底层重度盐渍化及以上的盐渍土约占20%,集中分布在研究区北部。
| [1] |
Zhu W, Yang J S, Yao R J, et al. Soil water-salt control and yield improvement under the effect of compound control in saline soil of the Yellow River Delta, China[J]. Agricultural Water Management, 2022, 263: 107455 DOI:10.1016/j.agwat.2022.107455 (  0) 0) |
| [2] |
Taghizadeh-Mehrjardi R, Schmidt K, Toomanian N, et al. Improving the spatial prediction of soil salinity in arid regions using wavelet transformation and support vector regression models[J]. Geoderma, 2021, 383: 114793 DOI:10.1016/j.geoderma.2020.114793 (  0) 0) |
| [3] |
Li Y S, Chang C Y, Wang Z R, et al. Remote sensing prediction and characteristic analysis of cultivated land salinization in different seasons and multiple soil layers in the coastal area[J]. International Journal of Applied Earth Observation and Geoinformation, 2022, 111: 102838 DOI:10.1016/j.jag.2022.102838 (  0) 0) |
| [4] |
解雪峰, 濮励杰, 沈洪运, 等. 滨海重度盐碱地改良土壤盐渍化动态特征及预测[J]. 土壤学报, 2022, 59(6): 1504-1516 (  0) 0) |
| [5] |
吴春生, 黄翀, 刘高焕, 等. 黄河三角洲土壤含盐量空间预测方法研究[J]. 资源科学, 2016, 38(4): 704-713 (  0) 0) |
| [6] |
McBratney A B, Odeh I O A, Bishop T F A, et al. An overview of pedometric techniques for use in soil survey[J]. Geoderma, 2000, 97(3/4): 293-327 (  0) 0) |
| [7] |
孙越琦, 孙笑梅, 巫振富, 等. 样点规模与采样方法对表层土壤pH空间预测精度的影响[J/OL]. 土壤学报, 2022: 1–17. (2022-10-11). https://kns.cnki.net/kcms/detail/32.1119.P.20221009.1741.002.html.
(  0) 0) |
| [8] |
Zhang S Y, Chen Y Y, Zhang Z Y, et al. VNIR estimation of heavy metals concentrations in suburban soil with multi- scale geographically weighted regression[J]. CATENA, 2022, 219: 106585 DOI:10.1016/j.catena.2022.106585 (  0) 0) |
| [9] |
Wang D, Li X X, Zou D F, et al. Modeling soil organic carbon spatial distribution for a complex terrain based on geographically weighted regression in the eastern Qinghai-Tibetan Plateau[J]. CATENA, 2020, 187: 104399 DOI:10.1016/j.catena.2019.104399 (  0) 0) |
| [10] |
Christakos G, Serre M L. BME analysis of spatiotemporal particulate matter distributions in North Carolina[J]. Atmospheric Environment, 2000, 34(20): 3393-3406 DOI:10.1016/S1352-2310(00)00080-7 (  0) 0) |
| [11] |
He J Y, Christakos G, Cazelles B, et al. Spatiotemporal variation of the association between sea surface temperature and chlorophyll in global ocean during 2002-2019 based on a novel WCA-BME approach[J]. International Journal of Applied Earth Observation and Geoinformation, 2021, 105: 102620 DOI:10.1016/j.jag.2021.102620 (  0) 0) |
| [12] |
He J Y, Christakos G, Wu J P, et al. Spatiotemporal BME characterization and mapping of sea surface chlorophyll in Chesapeake Bay (USA) using auxiliary sea surface temperature data[J]. Science of the Total Environment, 2021, 794: 148670 DOI:10.1016/j.scitotenv.2021.148670 (  0) 0) |
| [13] |
高凤杰, 吴啸, 师华定, 等. 基于贝叶斯最大熵的黑土区小流域土壤有机质空间分布预测[J]. 环境科学研究, 2019, 32(8): 1365-1373 (  0) 0) |
| [14] |
刘欢瑶, 孟岑, 邹冬生, 等. 基于BME-GWR法的景观单元土壤有机碳密度空间预测[J]. 广东农业科学, 2021, 48(2): 75-83 (  0) 0) |
| [15] |
Zhang C T, Yang Y. Can the spatial prediction of soil organic matter be improved by incorporating multiple regression confidence intervals as soft data into BME method?[J]. CATENA, 2019, 178: 322-334 DOI:10.1016/j.catena.2019.03.027 (  0) 0) |
| [16] |
Douaik A, Van Meirvenne M, Tóth T. Soil salinity mapping using spatio-temporal kriging and Bayesian maximum entropy with interval soft data[J]. Geoderma, 2005, 128(3/4): 234-248 (  0) 0) |
| [17] |
Xia J B, Ren J Y, Zhang S Y, et al. Forest and grass composite patterns improve the soil quality in the coastal saline-alkali land of the Yellow River Delta, China[J]. Geoderma, 2019, 349: 25-35 DOI:10.1016/j.geoderma.2019.04.032 (  0) 0) |
| [18] |
胡鑫隆, 齐继, 于千钧, 等. 黄河三角洲不同长势柽柳对土壤水盐异质性的影响[J]. 土壤, 2022, 54(6): 1291-1299 (  0) 0) |
| [19] |
王幼奇, 张兴, 赵云鹏, 等. 基于GIS和地理加权回归的砂田土壤阳离子交换量空间预测[J]. 土壤, 2020, 52(2): 421-426 (  0) 0) |
| [20] |
Allbed A, Kumar L, Aldakheel Y Y. Assessing soil salinity using soil salinity and vegetation indices derived from IKONOS high-spatial resolution imageries: Applications in a date palm dominated region[J]. Geoderma, 2014, 230/231: 1-8 DOI:10.1016/j.geoderma.2014.03.025 (  0) 0) |
| [21] |
Peng J, Biswas A, Jiang Q S, et al. Estimating soil salinity from remote sensing and terrain data in southern Xinjiang Province, China[J]. Geoderma, 2019, 337: 1309-1319 DOI:10.1016/j.geoderma.2018.08.006 (  0) 0) |
| [22] |
Masoud A A, Koike K, Atwia M G, et al. Mapping soil salinity using spectral mixture analysis of landsat 8 OLI images to identify factors influencing salinization in an arid region[J]. International Journal of Applied Earth Observation and Geoinformation, 2019, 83: 101944 DOI:10.1016/j.jag.2019.101944 (  0) 0) |
| [23] |
李海涛, 邵泽东. 空间插值分析算法综述[J]. 计算机系统应用, 2019, 28(7): 1-8 (  0) 0) |
| [24] |
Taghizadeh-Mehrjardi R, Minasny B, Sarmadian F, et al. Digital mapping of soil salinity in Ardakan region, central Iran[J]. Geoderma, 2014, 213: 15-28 (  0) 0) |
| [25] |
鲍士旦. 土壤农化分析(3版)[M].
中国农业出版社, 北京, 2000
(  0) 0) |
| [26] |
Wei Y, Ding J L, Yang S T, et al. Soil salinity prediction based on scale-dependent relationships with environmental variables by discrete wavelet transform in the Tarim Basin[J]. CATENA, 2021, 196: 104939 (  0) 0) |
| [27] |
Song C Y, Ren H X, Huang C. Estimating soil salinity in the Yellow River Delta, eastern China—An integrated approach using spectral and terrain indices with the generalized additive model[J]. Pedosphere, 2016, 26(5): 626-635 (  0) 0) |
 2024, Vol. 56
2024, Vol. 56


