2. 山东建筑大学建筑城规学院, 济南 250101
土地利用空间结构是指土地利用类型在地理空间上的分布和组织形式,人类活动包括农业、城市化和工业化等对生态系统的结构和功能以及生态系统服务的提供均产生巨大影响[1]。土地利用空间结构研究对于更好地理解土地利用格局和变化趋势、指导土地规划、促进可持续发展等具有重要的意义。
目前土地利用空间结构的定量计算包括土地利用分类统计、分形维数及稳定性指数的计算[2]。在土地利用分类统计方面,传统的遥感监测技术手段在处理土地利用分类问题时存在效率低下、预处理流程冗长及消耗存储等弊端。随着云存储和云计算技术的快速发展,谷歌地球引擎(Google earth engine, GEE)平台的出现为海量遥感数据的下载和处理提供了一种新的技术手段。GEE处理速度更快、数据集更丰富、分布式计算能力更强、可编程性更强、共享性更佳,为遥感工作者提供了极大的便利[3]。已有学者基于GEE平台对土地利用分类进行了相关研究,如Tassi等[4]基于GEE和Landsat-8影像绘制了2018—2020年意大利Maiella国家公园的土地利用/土地覆盖地图,发现基于对象的方法比基于像素的方法表现更好,添加纹理信息并不能改善后者;Yao等[5]在GEE平台上利用1990—2020年土地覆盖变化分析了中国新疆维吾尔自治区遥感生态指数的空间分布,发现其具有较高的效率,便于对生态环境质量进行快速、高频、宏观的监测;冯权泷等[6]基于GEE云平台利用Sentinel-1 SAR和Sentinel-2影像的光谱、纹理和极化特征研究了2021年黄淮海平原冬小麦的空间分布信息,对比了决策树、朴素贝叶斯、支持向量机和随机森林算法的分类结果,发现随机森林是4种机器学习算法中识别精度最高的分类器。上述研究证实了GEE平台在土地利用信息提取中的有效性。
在土地利用分类的基础上,利用分形理论计算分形维数及稳定性指数是土地利用空间结构研究的核心内容,其通过研究具有自相似结构的物体和空间,为地理学领域的土地利用空间结构研究提供了新的思路和方法。国内外学者基于分形理论对土地利用空间结构进行了大量研究,如Fernandez-Martinez和Sánchez-Granero[7]对分形维数的豪斯多夫理论进行了适当的离散化,建立了新的模型,进而计算了广义分形空间上子集的分形维数;Purevtseren等[8]运用分形几何学的数学程序和地理信息系统(GIS)的城市分析来描述了乌兰巴托市的土地使用情况,并使用面积和周长的指数关系衡量了城市的蔓延情况。部分学者从流域和城市的视角进行了研究,例如,李斌斌等[9]建立了流域像元尺度的栅格结构数字植被模型,并逐个计算得到各子流域植被格局分形维数;张荣天[10]利用分形理论和GIS空间分析方法,探讨了镇江市土地利用空间结构特征;Yu等[11]利用GIS数据研究了伦敦地区在城市和街区范围内的构成和配置异质性,揭示了土地覆盖和邻里类型的主要长度尺度以及具有最大信息增益的分辨率;吴涟敏等[12]在RS、GIS和统计分析工具的支持下,运用分形理论研究了时间序列上土地利用类型形态的复杂度与结构的稳定度,分析了土地利用空间格局的变化,从而阐述了不同土地利用类型的空间分布规律。
黄河三角洲是我国主要江河三角洲中最具重大保护价值的生态区域,其开发建设一直得到国内外广泛关注和支持[13]。然而,在黄河三角洲地区,由于历史原因、经济发展不平衡等因素,土地利用结构存在明显的不均衡现象,导致土地资源的不合理配置,造成不同类型的土地利用之间可能存在竞争和冲突,势必通过科学合理的规划和管理才能实现土地利用的协调和可持续发展[14]。因此,分析黄河三角洲生态功能保护区的土地利用空间结构变化具有重要意义。目前尽管有部分研究利用分形理论对城市空间结构及演变进行了分析,然则从生态功能保护区的视角对土地利用和分形理论两个领域交叉点的学术研究却较少,尤其是对黄河三角洲生态功能保护区的研究更是缺乏。另外,目前的研究时间尺度集中在20年以内,研究方法绝大多数采用的是传统的土地利用分类方法。
因此,本研究以黄河三角洲国家级生态功能保护区为例,采用随机森林分类方法对该区1985—2020年的土地利用类型进行划分,在此基础上利用分形理论方法计算土地利用分形维数和稳定性指数,分两个阶段定量讨论研究区近35年土地利用空间结构的复杂性和稳定性并分析其成因,以促进研究区土地资源的可持续利用,更好地理解人类活动和自然环境之间的相互作用,为土地管理、城市规划、生态保护等提供重要的理论和实践指导。
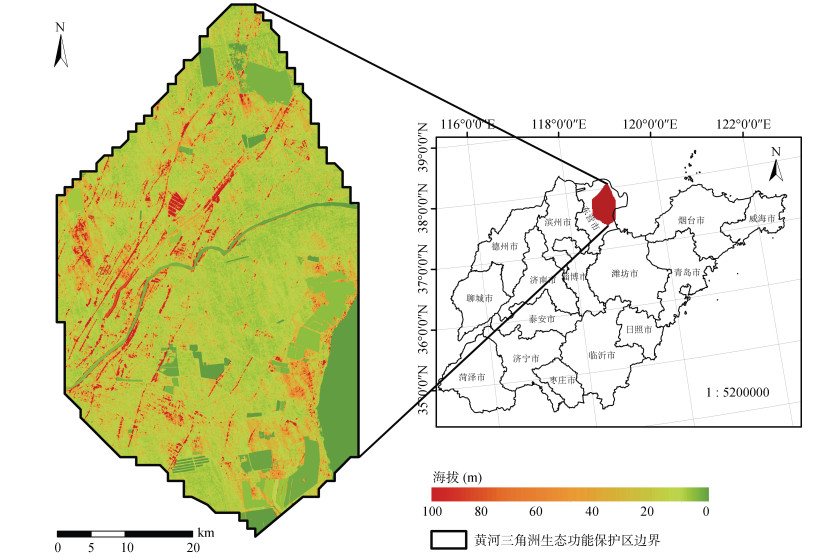
1 研究区概况与研究方法 1.1 研究区概况黄河三角洲是指黄河河口处形成的三角形河口平原,位于中国华北平原的东南部,如图 1所示。黄河三角洲生态功能保护区的地理坐标范围为37°27′30″N ~ 38°37′30″N,118°24′E ~ 119°09′E,可大致以东营市黄河入海口为中心,向东至黄河出海口、胶东湾,向北至黄河主干,向西至东营市区、垦利区,形成了一个广阔而独特的地理区域。该地区的总面积约1.15万km2,主要由三角洲前缘平原和黄河临海滩涂两部分组成[15],地形较为平坦,土层深厚,土壤肥沃,水系复杂,生态系统丰富多样。保护区致力于改善湿地生态环境,保障水资源,保护和繁衍当地的濒危物种,促进土地的可持续利用,以及促进区域生态系统的健康发展[16]。该地区拥有成百上千的港口和码头,是我国重要的贸易和通信中心之一,对全国的经济发展起着重要的支持和推动作用[17]。
|
图 1 黄河三角洲生态功能保护区区位示意图 Fig. 1 Location of Ecological Function Reserve in Yellow River Delta |
本研究选取1985—2020年的原始遥感影像来自美国地质调查局(https://www.usgs.gov/),传感器包括Landsat-5 MSS/TM、Landsat-7 ETM+、Landsat-8 OLI/TIRS,由罗切斯特理工学院(RIT)和美国国家航空航天局(NASA)喷气推进实验室(JPL)采用单通道算法创建,T1等级数据具有良好的辐射特征,并且在不同的Landsat传感器之间进行了相互校准,并被认为适合于时间序列分析。DEM数据来自NASA(https://lpdaac.usgs.gov/)发布的NASADEM,其是对STRM数据的再处理,通过纳入ASTER GDEM、ICESat GLAS和PRISM数据集的辅助数据,最重要的处理改进涉及通过改进相位解包和使用ICESat GLAS数据进行控制来减少空隙,提高了精度。具体数据如表 1所示。
|
|
表 1 数据集来源及参数 Table 1 Sources and parameters of dataset used |
在确定土地利用类型的种类和分类编码情况时,需要保证划分后的土地类型是相互独立且标准化的,针对黄河三角洲生态功能保护区缺乏林地的实际,参考自然资源部发布的最新标准GB/T 21010—2017《土地利用现状分类》[18],将该区域一级地类设置设为5类:耕地、草地、水体、裸地、建筑物(不透水面)。
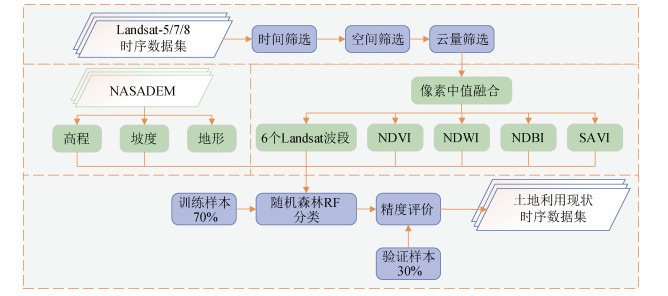
在GEE平台上,利用随机森林算法进行土地利用分类,其流程主要包括以下5个步骤:数据获取、数据处理、随机森林模型训练、分类结果生成以及结果评估。在GEE中,可以使用随机森林分类器API对影像进行分类,该API提供了一种灵活且高效的分类器实现方式,分类框架如图 2所示。
|
图 2 基于随机森林算法的土地利用分类框架 Fig. 2 Framework of land use classification based on random forest algorithm |
本研究经云量筛选(覆盖率 < 10%)后,选择每年5—9月作为影像选择的时间窗口。在目标年时间窗口中,筛选、去除云层和修复Landsat数据,并使用中位数合成方法合成研究区域的年度影像。除了Landsat本身的6个波段(蓝、绿、红、近红外、短波红外1、短波红外2),高程、坡度、NASADEM地形多样性数据和4个遥感指数(归一化建筑指数NDBI、归一化水体指数NDWI、土壤调节植被指数SAVI和归一化植被指数NDVI)被加入年度分类的特征集中。为进一步优化分类结果,本研究对每一年进行了10次分类,并将它们的众数合成。然后,在时间序列的分类结果中,使用众数时间滑动窗口(5年)进一步调整数据集的时间一致性。滑动窗口会将焦点年度的土地类别标签更新为时间窗口内所有类别标签的众数值。通过这些有效的分类和优化策略,最终,本研究生成了一套连续的黄河三角洲生态功能保护区空间分辨率为30 m的年度土地利用/覆被数据集。
在精度评价方面,本研究选取Kappa系数和总体精度(Overall accuracy, OA)作为评价指标[19]。总体精度是指被正确分类的总像元数与像元总数的比值,像元总数等于所有地类分类后的像元总和,被正确分类的像元为混淆矩阵的对角线对应的数值,计算公式为:
| $ {\text{OA}} = \frac{{\sum\limits_{I = 1}^n {Pij} }}{S} $ | (1) |
式中:n为行列数;Pij为第i行、第j列的元素;S为元素总和。
从公式(1)可以看出,总体精度的计算仅依靠混淆矩阵的对角线元素,无法全面衡量分类器的性能,因此,需要引入一种利用混淆矩阵所有元素来评价分类器性能的指标,即Kappa系数,计算公式为:
| $ {\text{Kappa}} = \frac{{S \cdot \sum\limits_{i = 1}^n {{P_{ij}}} - \sum\limits_{i = 1}^n {({P_{i + }} + {P_{ + j}})} }}{{{S^2} - \sum\limits_{i = 1}^n {({P_{i + }} + {P_{ + j}})} }} $ | (2) |
式中:n为行列数;Pij为第i行、第j列的元素;Pi+为行求和;P+j为列求和;S为所有元素的和。Kappa系数的取值位于–1 ~ 1,通常大于0,其大小与分类器性能的对应关系如表 2所示。
|
|
表 2 Kappa系数与分类质量的对应关系 Table 2 Correspondence of Kappa coefficient to classification quality |
土地利用转移矩阵是指一种用于描述土地利用变化和演变的数学模型,作为CA-MarKov模型预测分析的前期基础[20],通过对空间分布的土地利用类型进行调查与监测,可以得到不同时期的土地利用现状图。然后,通过对比不同时期的土地利用现状图,可以获得不同时期之间的土地利用变化。转移矩阵是一个n×n正方形矩阵,每一个元素Pij即代表土地利用类型i向土地利用类型j转移的面积。本文选择Origin 2022绘制得到土地利用转移图。
1.3.3 分形维数和稳定性指数统计分形维数是一个对于复杂几何体的量度,它的意义在于测量表征物体的复杂性[21]。分形维数可以被理解为是对于一个离散集合(如曲线或图案)中所有点的密度的量度。具体地讲,分形维数是可用于度量镶嵌形状的可度量参数,这个可度量参数被称作分形维数。分形维数概念最早由Mandelbrot和Van Ness[22]在1967年提出,其首先基于柯赛和定理中弗拉克图形的概念,提出了分形维数,其本质就是用分形维数计算具有自相似性质的复杂几何形状的维数。自相似性是指物体在不同大小的比例下,其形态和结构仍然相似。本研究中,将分形维数作为土地利用结构特征的一种定量指标,通过每一地类使用一种封闭的多边形斑块,并对其核心面积和边界曲折进行定量的描述[23]。
Mandelbrot和Van Ness[22]通过分析分形几何体结构形态构建了以下模型:
| $ {[S(r)]^{1/D}} \sim {[V(r)]^{1/3}} $ | (3) |
式中:V(r)代表体积;S(r)代表面积;r代表度量尺度;D代表分形维数。
董连科[24]在公式(3)的基础上提出了适用于计算n维欧氏空间的分形维数公式:
| $ {[S(r)]^{1/{D_{n - 1}}}} = {\text{k}}{{\text{r}}^{(n - 1 - {D_{n - 1}})/{D_{n - 1}}}}{[V(r)]^{1/n}} $ | (4) |
式中:当n=2时,即可研究二维空间中分形维数和周长与面积的关系。
对公式(4)两边同时取对数,得到双对数回归模型:
| $ \ln [A(r)] = \frac{2}{D}\ln [P(r) + C] $ | (5) |
式中:D代表土地利用结构的分形维数,即分维值;A(r)代表图斑的面积;P(r)代表图斑的周长;r代表空间测定尺寸;C为常数。
本研究采用双对数回归分析的方法,利用R语言将各土地利用类型斑块的周长和面积数据建立公式(5)所示的回归模型,通过回归系数计算分形维数D。D的取值范围为[1, 2],其大小可以反映研究区土地利用结构的稳定程度和复杂强度,D值越大,复杂度越高,图斑的形状越无规律。D值越接近1.5,稳定性越低,类似于分子运动越强烈,由此可以构建土地利用稳定性指数M:
| $ M = \left| {1.5 - D} \right| $ | (6) |
式中:M的取值范围为[0, 0.5],M值越大表明土地利用类型越脱离随机状态,稳定性越高,M值越小则相反。M值的变化可以反映研究区土地利用空间结构的变化趋势,故可用来预测未来的土地利用结构。
2 结果与分析 2.1 土地利用状况及精度评价如表 3所示,在精度评价方面,选择70% 的样本进行训练,30% 的样本用于精度检验。经统计,历年的土地利用分类总体精度均在85% 以上,Kappa系数均在0.8以上,经目视判读,低覆盖度的草本植物因光谱特征与收获后的农田相似,使得耕地容易被误分类为草地。基于不同的特征进行随机森林分类的Kappa系数均大于0.8,OA均在80% 以上,说明分类器性能极好,其中分类方案3的精度最好,Kappa系数为0.83,OA为87%,故选择此方案进行土地利用分类。
|
|
表 3 不同特征组合下随机森林分类精度评价 Table 3 Accuracy assessment of random forest classification under different feature combinations |
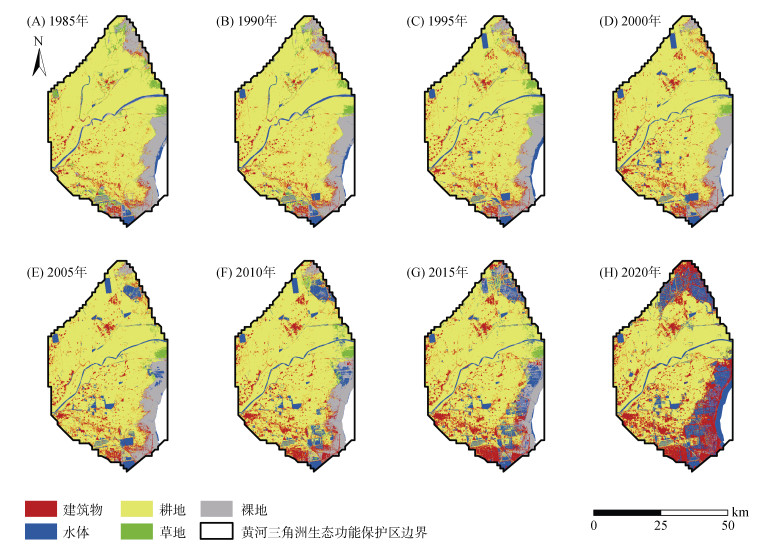
本研究选取黄河三角洲生态功能保护区1985—2020年5—8月的遥感影像进行土地利用分类。为了更好地突出植被,QA波段标记了Landsat影像云及其阴影的信息,用于去云处理。土地利用分类结果如图 3所示。由图 3可以看出,土地利用分类结果基本符合黄河三角洲生态功能保护区的实际,建筑物主要分布在南部东营市区、西南部垦利区以及北部的仙河镇;河流为中部穿过的黄河,较大的水库主要有:广南水库、广北书库、永镇水库、孤河水库、孤东水库、孤北水库等;耕地沿黄河两岸大致呈对称分布,这与引黄河水进行灌溉密不可分;裸地绝大部分分布在北部神仙沟地区以及保护区东南部,沿着莱州湾,北至大汶流海堡,南抵南海铺,呈月牙形状分布。
|
图 3 1985—2020年研究区土地利用分类结果 Fig. 3 Results of land use classification from 1985 to 2020 in study area |
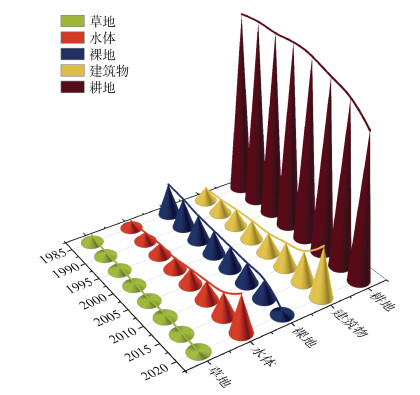
如图 4和表 4所示,黄河三角洲地势平坦,土地肥沃,适宜农业生产,因此,农业占据了这一地区绝大部分的土地利用面积。河口三角洲地区的水系非常发达,河流纵横交错。这一特征既为农田提供了灌溉水源,也为当地生态系统的形成提供了便利。35年来,水体面积逐步扩大,2015—2020年增长率达60%。2008—2015年,山东连续推行黄河三角洲湿地和刁口河生态补水项目,持续补水3.8亿m3,推动了湿地植被的顺向演变,鸟类栖息地面积逐渐恢复。2018—2019年,河道外生态式引水5.26亿m3,着重保护黄河三角洲湿地,保障了滨州重盐碱地区的生态补水。2005年之前,耕地面积无显著变化,维持在1 750 km2;2005—2020年,耕地面积急剧下降,减少了约300 km2。草地面积降低速率缓慢,约占总面积的2.9%。建筑物面积大致呈指数增长,主要集中在东营市区和莱州湾地区。裸地面积在2015—2020年骤降150 km2,表明黄河三角洲实行生态保护的成果显著,这与当地2017年实施创新驱动发展战略、新旧动能转换和深化体制改革政策密不可分[25]。
|
图 4 1985—2020年研究区土地利用面积变化 Fig. 4 Area changes of land use types in study area from 1985 to 2020 |
|
|
表 4 1985、2005、2020年研究区土地利用状况 Table 4 Status of land use types of study area in 1985, 2005 and 2020 |
某些现象可能在长时间范围内经历多个阶段性的变化和发展,具有一定的非线性性质,忽略其中的变化和演变过程,将长时序研究分成两个阶段可以更好地捕捉变化的轨迹和模式,有助于理解现象或事件的发展趋势和变化机制。为了便于分析,本文以15年为间隔,将1985—2020年分成两个阶段:1985—2005年为第一阶段,2005—2020年为第二阶段。两个阶段的土地利用类型转移如图 5所示。
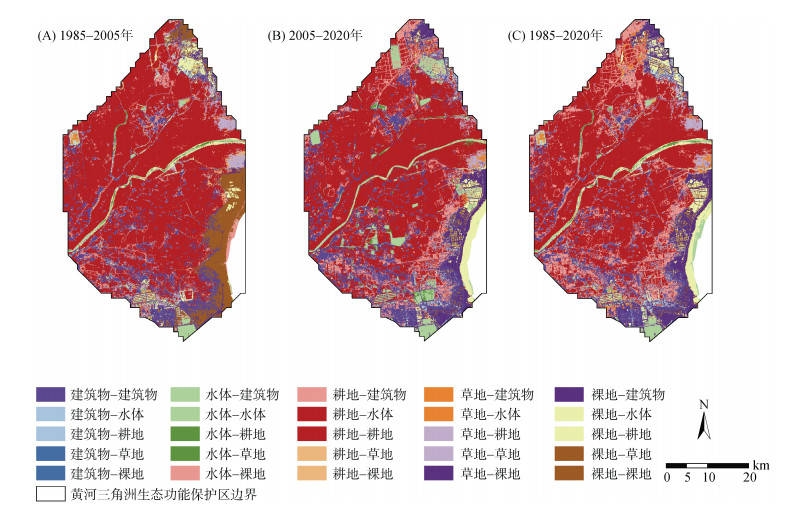
|
图 5 1985—2020年研究区土地利用类型转移情况 Fig. 5 Transfer among land use types from 1985 to 2020 in study area |
为定量研究黄河三角洲生态功能保护区各个时期土地利用的定量转移情况,分别构建1985—2005年、2005—2020年和1985—2020年的转移矩阵,研究区土地利用定量转移关系如图 6所示。
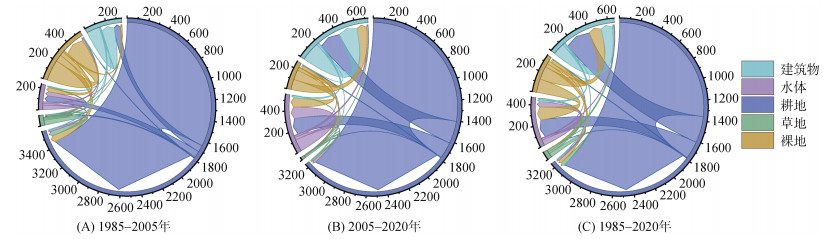
|
图 6 三个时期研究区土地利用转移矩阵 Fig. 6 Transfer matrix of land use types in three periods in study area |
由图 5和图 6可知,第一阶段:1985年,黄河三角洲生态功能保护区的耕地占据了绝对的优势地位,占全部土地利用面积的66.5%。同时,裸地也占了相当一部分比例,约18.3%,而草地面积约占10.2%,水体和建筑物面积分别为4.1% 和0.9%。综合来看,农业生产和城市建设在当时占据了绝对主导地位。2005年,耕地、草地以及水体和建筑物面积均有所增加,而裸地的面积则有所减少,水体和建筑物50% 左右由耕地转化而来,耕地面积增加的部分主要来自裸地和草地。第二阶段:2020年,研究区耕地面积相比2005年有所减少,主要转移成水体和建筑物。而草地和水体的面积增加较为明显,分别增加了1.5倍和2.7倍。建筑物面积也继续快速增长,从2005年的208.45 km2增加到了520.66 km2。裸地面积则降至39.03 km2,与1985年相比,降幅达到了87.96%。上述变化说明城市化和经济发展的推进对土地利用的影响逐渐显现。这一结论与王永丽等[26]的研究结论一致。
2.3 分形维数和稳定性指数时空变化利用GIS计算1985、2005、2020年各地类图斑的面积和周长,利用R语言建立双对数回归模型,将面积和周长取自然对数,分别作为Y轴和X轴,将散点拟合成关于面积–周长的线性函数,得到判断系数R2和斜率2/D,进而得到分形维数D的数值,如表 5所示。从表 5中可以看出,各地类及总体的R2检验值均大于0.96,说明拟合效果较好,表明研究区各用地类型的面积–周长显著线性相关,分形维数具有代表意义。研究区各地类总体分形维数和稳定性指数在第一和第二阶段的变化趋势相同,分形维数均呈现降-增趋势,稳定性指数均呈现增-降趋势,且变化率均有明显降低。
|
|
表 5 1985、2005、2020年各地类的分形维数和稳定性指数 Table 5 Fractal dimension and stability index for each land use type in 1985, 2005 and 2020 |
对于耕地,如表 5所示,1985年,研究区的总分形维数为1.216,而耕地的分形维数为1.223,略高于总体水平;稳定性指数为0.277,低于总体水平,表明相对于其他土地利用类型,耕地形态较为简单,但不够稳定。2005年,从总体分形维数1.182开始,耕地的分形维数下降至1.206,稳定性指数上升至0.294,从而实现了稳定性方面的提高。至2020年,虽然耕地的分形维数略有上升(1.207),但稳定性指数也略有下降(0.293),表明在当前的土地政策下,研究区的耕地可能出现了一些相对不稳定的情况。究其原因,20世纪80年代末至90年代初,我国政府逐步实行了一系列耕地保护政策,以鼓励开垦荒地和草地,于增加耕地供给[27]。这一政策的影响是,相比之前的情况,1985年耕地的分形维数略高,而稳定性指数较低,而2005年稳定性指数的提高可能与政府进一步加强耕地保护有关[28]。
对于草地,1985年,草地的分形维数为1.229,略高于总体分形维数,而稳定性指数为0.271,略低于总体稳定性指数(表 5),表明草地的形态相对较为复杂,较不稳定。2005年,草地的分形维数下降至1.168,稳定性指数上升至0.332,形态变得更简单,稳定性更高。至2020年,草地的分形维数又上升至1.230,但其稳定性指数下降至0.270,表明草地变得更为复杂,稳定性下降。究其原因,2000年以后,中国的城市化进程加速,推动城市建设和新型城镇化等政策不断推进。城市化的进程导致了大量的草地消失,草地面积受到了很大程度的压缩。而对草地的保护在一定程度上又取决于草原法的修订、地方政府和政府部门的具体的政策和实践[27]。这种政策的影响可能导致了2020年草地变得更为复杂,不够稳定。
对于水体,1985年,水体的分形维数为1.206,略低于总体分形维数,而稳定性指数为0.294,高于总体稳定性指数(表 5),表明水体的形态相对简单,稳定性高。2005年,水体的分形维数下降至1.174,稳定性指数上升至0.326,表明水体形态更为简单,稳定性得到了提高。至2020年,水体的分形维数略升至1.195,稳定性指数又下降至0.305,表明水体的形态复杂略微上升,稳定性略有下降。究其原因,在过去几十年中,中国的环保政策日益完善,合理利用水资源,保护水体生态环境成为政府工作的重点[29]。在一定程度上,环保政策和水土保持政策的实施改善了水体的形态和稳定性。
对于裸地,1985年,裸地的分形维数为1.283,高于总体分形维数,而稳定性指数为0.217,远低于总体稳定性指数(表 5),表明裸地形态非常复杂,且稳定性较差。2005年,裸地的分形维数下降至1.232,稳定性指数上升至0.268,表明裸地的形态变得更为简单,稳定性得到了提高。至2020年,裸地的分形维数和稳定性指数分别为1.229和0.271,相比2005年基本没有变化。究其原因,自20世纪90年代以来,我国的生态保护意识日益增强,不断加强了对裸地的治理和保护。草原退化防治、退耕还林还草、荒漠化防治和水土保持四大工程的实施均为解决裸地问题提供帮助[27]。
对于建筑物,表 5数据显示,1985年,建筑物的分形维数为1.183,略低于总体分形维数,而稳定性指数为0.317,高于总体稳定性指数,表明建筑物的形态相对较为简单,稳定性高。2005年,建筑物的分形维数下降至1.167,稳定性指数上升至0.333,表明建筑物的形态变得更为简单,稳定性得到了提高。至2020年,建筑物的分形维数又上升至1.176,但稳定性指数又下降至0.324,表明建筑物的形态复杂化程度较2005年有所上升,同时稳定性也略有下降。究其原因,在2000年之后中国城市化进程加速推进,建设政策也发生了变化,导致建筑用地大量增加,进而导致土地的不稳定性进一步提高[27]。与此同时,当地有关部门出台了一系列环境保护政策,这些政策有助于改善水体和草地的稳定性,但可能也会对耕地和建筑用地产生负面影响[29]。
3 讨论分形维数及稳定性指数的研究前提是较好的土地利用分类结果,所以对遥感影像数据源及分类方法和精度的要求很高,单期影像虽然可以满足云量低的要求,但不可避免地会存在像元异常值的问题。与其他仅使用单期影像的分类研究相比[30],本研究基于GEE平台,利用中值合成算法去除同年份多期影像像元异常值,提高了1985—2020年Landsat-5(TM)、Landsat-7(ETM)和Landsat-8(OLI)的长时间影像序列的质量。与其他研究仅使用影像本身的波段相比[31],本研究还引入了4种遥感指数和3种地形因子,分类的总体精度由80% 提高到85%。
对比其他相关研究,本研究的时间尺度较长,能够更好地反映该地区土地利用空间结构的变化特征。1985年,黄河三角洲生态功能保护区的耕地占据了绝对的优势地位,占到了全部土地利用面积的66.5%。2005年,耕地、草地以及水体和建筑物面积均有所增加,而裸地的面积则有所减少。2020年,耕地面积相比2005年有所减少,主要转移成了水体和建筑物。综合来看,随着城市化和经济发展的推进,土地利用发生了一定的变化,农业生产逐渐向城市化方向转变。这些变化反映了土地利用结构的变化趋势,这与陈雪萍等[32]、周建等[33]的研究基本一致。
相比于流域尺度和城市尺度的研究视角,本研究从生态保护区的视角结合分形理论研究了土地利用空间结构变化。研究区总体的分形维数在第一、二阶段的变化量分别是–0.033 8和0.009 2,稳定性指数的变化量分别是0.034和–0.009,表明两结果能较好地互相吻合,说明研究区的土地利用空间结构趋于稳定,土地利用类型之间的关联性变弱,土地利用类型之间的替代程度变高。这与陆智博等[17]的研究结果基本一致。
本文仅通过分形维数和稳定性指数进行分析,并没有纳入其他景观格局指数,因此结果可能不够精确和全面。如何综合运用各种指标来分析土地利用空间结构的变化,以及考虑空间异质性对指数计算带来的影响,将是本研究后续探讨的一个重要方向。在今后的研究中,可以考虑研究土地利用变化对生态环境的影响及城市化的空间格局对土地利用类型和空间结构的影响,既包括城市扩张对农田的压缩,也包括城市用地的类型和结构演变。
4 结论本研究基于GEE处理平台和随机森林分类方法,解译并分析了黄河三角洲生态功能保护区1985—2020年的离散土地利用。利用1 250个样本点对Landsat影响进行土地利用分类处理,结果表明,分类精度极好,近35年5个一级地类的总体精度达85%以上,Kappa精度在0.8以上。1985—2020年,研究区耕地面积逐渐下降;草地面积变化较小;水体面积扩大,且增长率在2015—2020年之间比较明显;裸地面积变化较为剧烈,先增长后逐渐下降,最高峰出现在2005年,最低谷出现在2020年;建筑物面积发生了显著变化,增长率较高。从土地利用转移矩阵来看,2020年的耕地和水体50% 左右的面积由1985年的耕地转化而来,其中水体另一半面积主要来自裸地,建筑物近1/4的面积来自裸地。。
黄河三角洲生态功能保护区1985年、2000年和2020年土地利用的总分形维数分别为1.216、1.182和1.191,总体上呈现降低趋势,说明研究区的土地利用空间结构复杂度降低,图斑形状越来越规律;稳定性指数分别为0.284、0.318和0.39,总体呈升高趋势,说明研究区空间利用结构稳定性升高。从总体变化可以看出,土地利用空间结构与当地政策呈正相关,研究区生态功能愈来愈强大,空间布局愈来愈合理。其中,从耕地、水体和裸地的分形维数和稳定性指数可以看出,空间结构和稳定性朝正向发展,这与当地耕地保护、水土保持、荒漠化防治政策息息相关。然而,草地和建筑物的空间结构和稳定性朝负面发展,相关部门应该着手把控城市化进程和加快草地保护的立法进程,避免两者的无序扩张与收缩,以推动植被的顺向演变。
| [1] |
谢贤健. 基于GIS和分形理论的沱江流域土地利用结构动态分析[J]. 土壤, 2023, 55(2): 433-440 (  0) 0) |
| [2] |
浩飞龙, 吴潇然, 关皓明, 等. 基于百度迁徙数据的东北地区城市"层级–网络" 结构[J]. 地理科学, 2023, 43(2): 251-261 (  0) 0) |
| [3] |
郝斌飞, 韩旭军, 马明国, 等. Google Earth Engine在地球科学与环境科学中的应用研究进展[J]. 遥感技术与应用, 2018, 33(4): 600-611 (  0) 0) |
| [4] |
Tassi A, Gigante D, Modica G, et al. Pixel- vs. object-based landsat 8 data classification in google earth engine using random forest: The case study of maiella National Park[J]. Remote Sensing, 2021, 13(12): 2299 DOI:10.3390/rs13122299 (  0) 0) |
| [5] |
Yao K X, Halike A, Chen L M, et al. Spatiotemporal changes of eco-environmental quality based on remote sensing-based ecological index in the Hotan Oasis, Xinjiang[J]. Journal of Arid Land, 2022, 14(3): 262-283 DOI:10.1007/s40333-022-0011-2 (  0) 0) |
| [6] |
冯权泷, 任燕, 姚晓闯, 等. 基于多源光学雷达数据融合的黄淮海平原冬小麦识别[J]. 农业机械学报, 2023, 54(2): 160-168 (  0) 0) |
| [7] |
Fernández-Martínez M, Sánchez-Granero M A. Fractal dimension for fractal structures: A Hausdorff approach[J]. Topology and Its Applications, 2012, 159(7): 1825-1837 DOI:10.1016/j.topol.2011.04.023 (  0) 0) |
| [8] |
Purevtseren M, Tsegmid B, Indra M, et al. The fractal geometry of urban land use: The case of ulaanbaatar city, Mongolia[J]. Land, 2018, 7(2): 67 DOI:10.3390/land7020067 (  0) 0) |
| [9] |
李斌斌, 李占斌, 李鹏. 基于GIS与RS的大理河流域植被格局分形维数时空变化特征[J]. 农业工程学报, 2015, 31(12): 173-178 (  0) 0) |
| [10] |
张荣天. 宁镇扬丘陵区土地利用空间结构的分形研究——以镇江市为例[J]. 水土保持研究, 2013, 20(3): 98-103 (  0) 0) |
| [11] |
Yu T F, Sützl B S, van Reeuwijk M. Urban neighbourhood classification and multi-scale heterogeneity analysis of Greater London[J]. Environment and Planning B: Urban Analytics and City Science, 2023, 50(6): 1534-1558 DOI:10.1177/23998083221140890 (  0) 0) |
| [12] |
吴涟敏, 廖善刚. 基于GIS和分形理论的土地利用空间格局分析——以闽侯县为例[J]. 地球环境学报, 2019, 10(2): 156-165 (  0) 0) |
| [13] |
Dong J B, Wu Y, Jin Y, et al. Morphology differences between fractional Brownian motion and the Weierstrass-Mandelbrot function and corresponding Hurst evaluation[J]. Geomechanics and Geophysics for Geo-Energy and Geo-Resources, 2023, 9(1): 35 DOI:10.1007/s40948-023-00532-4 (  0) 0) |
| [14] |
麦丽开·艾麦提, 满苏尔·沙比提, 张雪琪, 等. 叶尔羌河平原绿洲土地利用变化及土地生态安全评价研究[J]. 土壤, 2019, 51(4): 795-802 (  0) 0) |
| [15] |
李珊, 杨越超, 姚媛媛, 等. 不同土地利用方式对山东滨海盐碱土理化性质的影响[J]. 土壤学报, 2022, 59(4): 1012-1024 (  0) 0) |
| [16] |
陆蕴青, 向伟, 李敏, 等. 黄土塬区土地利用变化对地表蒸散的影响[J]. 土壤学报, 2023, 60(1): 89-98 (  0) 0) |
| [17] |
陆智博, 宋芊, 赵健赟, 等. 黄河源区2005—2020年生态用地格局变化与分异趋势[J]. 水土保持通报, 2022, 42(6): 277-284 (  0) 0) |
| [18] |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化路理委员会. 土地利用现状分类: GB/T210l0—2017[S]. 北京: 中国标准版社, 2017.
(  0) 0) |
| [19] |
Yi L N, Zhang G F. Object-oriented remote sensing imagery classification accuracy assessment based on confusion matrix[C]//2012 20th International Conference on Geoinformatics. Hong Kong, China. IEEE, 2012: 1–8.
(  0) 0) |
| [20] |
马银, 郑敏睿, 郑新奇, 等. 基于CA-Markov和MSPA的绿色基础设施预测与时空演变分析——以京津冀城市群为例[J]. 生态学报, 2023, 43(16): 6785-6797 (  0) 0) |
| [21] |
佘洁, 石云, 赵娜, 等. 土壤养分的空间变异性研究进展[J]. 山东农业科学, 2023, 55(1): 165-172 (  0) 0) |
| [22] |
Mandelbrot B B, Van Ness J W. Fractional Brownian motions, fractional noises and applications[J]. SIAM Review, 1968, 10(4): 422-437 DOI:10.1137/1010093 (  0) 0) |
| [23] |
蔡俊杰, 李希建, 谢洪高. 基于分形理论的上覆煤岩裂隙发育规律研究[J]. 矿业研究与开发, 2023, 43(1): 109-114 (  0) 0) |
| [24] |
董连科. 分形生长动力学中的两种非线性模型[J]. 地球科学, 1993, 18(1): 95–99, 127 (  0) 0) |
| [25] |
吴春生, 黄翀, 刘高焕, 等. 基于模糊层次分析法的黄河三角洲生态脆弱性评价[J]. 生态学报, 2018, 38(13): 4584-4595 (  0) 0) |
| [26] |
王永丽, 于君宝, 董洪芳, 等. 黄河三角洲滨海湿地的景观格局空间演变分析[J]. 地理科学, 2012, 32(6): 717-724 (  0) 0) |
| [27] |
孔梅, 曹惠明, 高兴国, 等. 黄河三角洲自然保护区国土空间变化遥感监测与评价[J]. 海洋环境科学, 2021, 40(2): 272-276 (  0) 0) |
| [28] |
孙丹丹, 刘学, 杨继松, 等. 黄河三角洲农田退耕年限对土壤不同形态氧化铁含量及其分布的影响[J]. 生态学杂志, 2023, 42(10): 2359-2367 (  0) 0) |
| [29] |
高瑞, 王志勇, 周晓东, 等. 利用多时相遥感监测与分析黄河三角洲湿地变化动态[J]. 测绘通报, 2021(4): 22-27 (  0) 0) |
| [30] |
陈大蓉, 周旭, 胡锋, 等. 近30年贵阳市土地利用冲突时空变化分析[J]. 水土保持研究, 2023, 30(6): 337–344, 356 (  0) 0) |
| [31] |
Zhao X Y, Xia H M, Liu B Y, et al. Spatiotemporal comparison of drought in shaanxi–gansu–ningxia from 2003 to 2020 using various drought indices in google earth engine[J]. Remote Sensing, 2022, 14(7): 1570 DOI:10.3390/rs14071570 (  0) 0) |
| [32] |
陈雪萍, 赵学勇, 王瑞雄, 等. 气候变化与土地利用/覆被变化对中国北方农牧交错带水资源影响研究进展[J]. 中国沙漠, 2022, 42(3): 170-177 (  0) 0) |
| [33] |
周建, 张凤荣, 徐艳, 等. 基于降水量与土壤类型的北方农牧交错区土地利用/覆被格局及变化分析——以科尔沁左翼后旗为例[J]. 地理研究, 2017, 36(7): 1210-1222 (  0) 0) |
2. School of Architectural and Urban Planning, Shandong Jianzhu University, Jinan 250101, China
 2024, Vol. 56
2024, Vol. 56


