2. 西北农林科技大学水土保持研究所, 陕西杨凌 712100
雨滴击溅侵蚀是造成水土流失的重要因素[1]。研究表明,雨滴冲击作用引起土壤团聚体分散破碎,导致土壤孔隙堵塞和入渗能力降低[2]。土壤结构对土壤的渗透性、通气性和植物的养分利用等都具有重要的影响。土壤入渗过程是土壤水分运动的关键环节,影响着土壤侵蚀程度与植被生长状况[3-4]。探究雨滴击溅下土壤结构与入渗能力的相互作用机制,对生态建设与农业发展具有重要意义。
雨滴击溅可导致土壤团聚体破碎分离[1]和土壤孔隙度降低[5],其中大团聚体周围产生的微团聚体碎片是造成土壤孔隙堵塞的主要因素[6]。雨滴击溅下土壤团聚体的破碎和分离程度不仅取决于雨滴能量[7],还受土壤渗透能力影响[8]。研究表明,较高的降雨强度可以显著降低土壤渗透能力[9-10]。Basset等[11]通过收集相关论文并从中提取元数据进行分析,发现渗透率与土壤结构特性(容重、团聚体稳定性、平均重量直径、有机碳含量和孔隙率等)之间存在显著的相关性。土壤孔隙空间及其结构特征是控制土壤中水和溶质运动的重要因素,开展孔隙结构的量化研究对于预测土壤水力性质具有重要意义[12]。土壤孔隙结构可量化为孔隙大小分布、形状和连通性[13]。目前有关雨滴击溅对土壤孔隙连通性影响的研究较少,且对于降雨过程中土壤孔隙微观结构与入渗能力的关系认识还不够清晰。孔隙网络模型(Pore network model,PNM)加深了对多孔介质中传输和流动的理解[14],为定量化分析土壤孔隙连通状况提供了思路[15-16]。
因此,本研究基于雨滴击溅试验、土壤饱和渗透试验,并结合计算机断层扫描(Computed Tomography,CT)与图像处理技术,以黄土高原典型农用地土壤褐土为研究对象,探究了不同直径大小雨滴击溅下表层土壤孔隙大小、形状和连通性特征,并基于PNM定量分析了不同降雨条件下表层土壤孔隙微观结构与土壤入渗能力的关系,以揭示击溅侵蚀机理,为农业及生态环境发展提供理论依据。
1 材料与方法 1.1 样品采集土壤样品采集于陕西省宝鸡市眉县的农耕地(107°45′36″ E,34°29′24″),样区年平均气温为12.9 ℃,年平均降水量为609.5 mm。采集土壤样品时,按照对角线法布设采样点,去除地面落叶杂物后,使用直径10 cm、高5 cm的环刀,取表层(0 ~ 10 cm)的原状土样。取样结束后,用滤纸垫于环刀底部,用保鲜膜包裹环刀以避免水分蒸发和运输过程中土样洒落,同时运输过程减少颠簸以免破坏土壤结构。供试土壤理化性质见表 1。
|
|
表 1 供试土壤基本理化性质 Table 1 Physiochemical properties of tested soils |
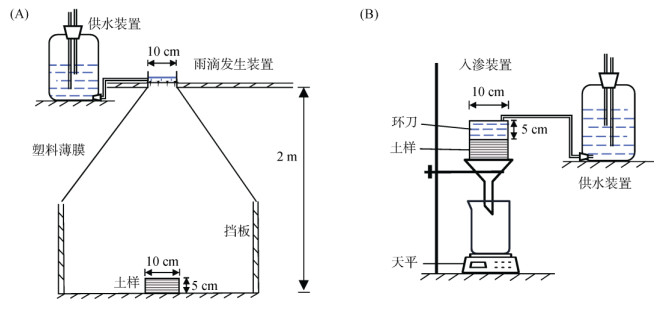
本研究基于可变针头式降雨装置(图 1A)模拟雨滴击溅。雨滴发生装置距离地表 2 m,通过控制针头的型号模拟不同直径的雨滴击溅,雨滴参数及计算方法见文献[17]。设置无雨滴击溅(CK)、2.67 mm直径雨滴击溅(SR-2.67)、3.39 mm直径雨滴击溅(SR-3.39)和4.05 mm直径雨滴击溅(SR-4.05)四个处理,每个处理重复3次,降雨时长10 min。模拟降雨试验之前,将样品饱和8 h,再静置12 h,以保证样品具有相近的含水率。将采集的土样放置在测试区,为防止雨滴降落过程中受到横向气流扰动,整个试验装置外围布设遮挡塑料薄膜。
|
(A:模拟降雨试验;B:土壤渗透试验) 图 1 试验装置示意图 Fig. 1 Diagrams of test devices |
|
|
表 2 不同直径雨滴击溅对表土孔隙结构参数的影响 Table 2 Effects of raindrop splashing with different diameters on topsoil pore structure parameters |
土壤渗透试验采用环刀法进行,试验装置示意图如图 1B所示。测量前将1.2中处理后的土样置于适当高度的水中进行充分饱和,以排除土壤中空气对水流入渗的影响。之后在土壤样品上方对接1个空环刀,并使用防水胶带将两个环刀粘连在一起,两环刀接触面用凡士林涂抹密封,确保对接部分不会漏水。将组装好的双环刀固定在铁架台上,并在其下方放置滤纸、漏斗、烧杯和天平,测定土壤入渗量。将薄海绵片放置在环刀内,阻挡水流对土样的破坏。通过马氏瓶向双环刀供水并保持5 cm的水头高度,同时用温度计测量水温。待漏斗滴下第1滴水开始计时,前10 min每隔1 min记录1次天平读数,之后每隔5 min记录1次天平读数,持续记录1 h。
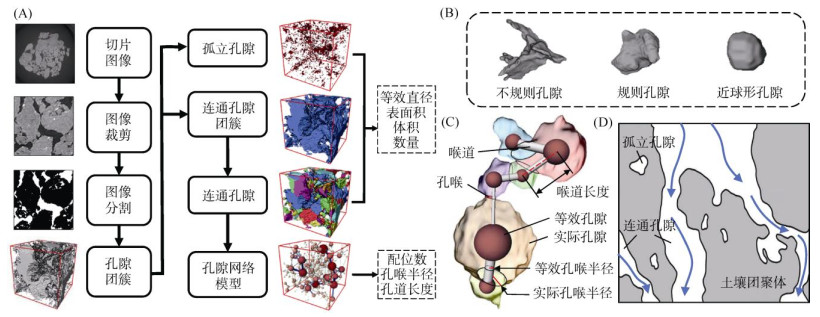
1.4 CT扫描及图像处理入渗试验结束后,将环刀内土壤样品自然风干,从CK、SR-2.67、SR-3.39和SR-4.05四个处理土壤表层取干土块(2 mm×2 mm×2 mm),将土块保存在装有海绵的容器中,以保持其结构完整性。共选取12个干土块样品用于CT扫描。采用上海光源X射线成像及生物医学应用光束线站(BL13W1)的同步辐射显微CT进行扫描,每个样品获得约1 600张像素为2 048×2 048的32位tiff格式切片图像,图像分辨率为3.25 μm,详细扫描方法及参数见文献[5]。CT图像处理流程见图 2A,采用Python的NumPy软件包进行切片图像的裁剪和格式转换。为避免图像边缘对分析结果的影响,选取土块中心区域512×512×512像素(边长为1.664 mm的正方体)作为研究区域进行分析;图像的预处理、分割、孔隙几何属性(体积、表面积和等效直径)的计算以及孔隙网络模型的构建基于Avizo2020.1软件实现。采用中值滤波算法去除图像中的噪声,借助边缘增强算法对土壤固相和孔隙交界处的灰色过渡带进行边缘增强处理。使用阈值分割(interactive thresholding)算法,结合Top hat图像分割算法进行图像分割,以区分土壤固相和土壤孔隙。
|
(A:CT图像处理技术流程;B:孔隙形状示意图;C:孔隙网络模型示意图;D:土壤孔隙局部渗流示意图) 图 2 土壤孔隙微观结构分析方法 Fig. 2 Analysis methods of soil pore microstructure |
由于土壤颗粒间不同的接触关系[18],根据土壤孔隙连通状况可分为连通孔隙(Connected pore, CP)和孤立孔隙(Isolated pore, IP) (图 2D)。连通孔隙是指由相互连接的孔隙组成的土壤孔隙团簇,对土壤水分和养分运移与气体交换具有重要作用。孤立孔隙是指不与其他孔隙相连接的、孤立的、碎片化的孔隙,主要影响土壤持水能力和有机碳物理保护能力[16]。对分割后的切片图像进行三维重建,得到土壤孔隙团簇的三维结构。孔隙团簇即土壤孔隙三维结构中互不相连的像素集合体,包含孤立孔隙团簇和连接三维数据体上下表面的连通孔隙团簇。孤立孔隙体积、表面积和等效直径(孔隙等体积球体的直径)可以直接通过Avizo软件的Label Analysis模块计算,而连通孔隙几何特征需要对连通孔隙团簇分割后计算,基于Axis Connectivity模块提取连通孔隙团簇,并使用Separate模块对连通孔隙团簇进行分割,以识别相邻连通孔隙之间的边界[19]。为了确定各连通孔隙之间的连接关系,在对连通孔隙进行分割的基础上,采用Generate Pore Network Model模块提取等效孔隙网络,建立孔隙网络模型。
1.5 数据处理与分析土壤入渗特征参数的计算方法如下[20]:
| $ Q = \frac{{10\sum\limits_{i = 1}^n {{Q_n}} }}{S} $ | (1) |
式中:Q为累积入渗量(mm);Qn为单位时间渗出水量(cm3);S为环刀横截面积(cm2)。
| $ v = \frac{{10{Q_n}}}{{{t_n} \cdot S}} $ | (2) |
式中:v为入渗速率(mm/min),根据土壤入渗过程中的入渗速率变化特征,将入渗过程划分为初始入渗阶段(0 ~ 10 min)和稳定入渗阶段(30 ~ 60 min),并计算不同处理下土壤的初始入渗率和稳渗速率,初始入渗率和稳渗速率分别为初始入渗阶段和稳定入渗阶段的平均入渗速率;tn为单位入渗间隔时间(min)。
| $ {K_T} = {v_{\text{s}}} \cdot \left( {\frac{L}{{h + L}}} \right) $ | (3) |
| $ K = {v_{\text{s}}} \cdot \left( {\frac{L}{{h + L}}} \right) \cdot \left( {\frac{1}{{0.7 + 0.03T}}} \right) $ | (4) |
式中:KT为温度为T℃时的土壤渗透系数(mm/min);K为温度为10℃时的土壤渗透系数(mm/min);vs为稳渗速率(mm/min);h为环刀内水头高度(cm);L为土层厚度(cm);T为试验水温(℃)。
本研究以土壤总孔隙度表征土壤孔隙体积占土壤总体积的比例,计算公式为:
| $ {P_T} = \frac{{{V_p}}}{{{V_s}}} $ | (5) |
式中:PT表示总孔隙度;Vp表示土壤孔隙总体积(μm3);Vs表示土壤总体积(μm3)。
土壤孔隙大小以其等效直径表示,将土壤孔隙按其等效直径分为5种类型:≤25 μm(小孔隙)、25 ~ 50 μm(中小孔隙)、50 ~ 75 μm(中孔隙)、75 ~ 100 μm(大中孔隙)和 > 100 μm(大孔隙)[5],并计算各等效直径级别孔隙的孔隙率,各类孔隙的孔隙率计算见公式(6)。
| $ {P_x} = \frac{{{V_x}}}{{{V_p}}} $ | (6) |
式中:x表示孔隙类型;Px表示该类孔隙的孔隙率;Vx表示土壤中该类孔隙的总体积(μm3);Vp表示土壤孔隙总体积(μm3)。
为确定雨滴击溅下表层土壤孔隙的形状特征,引入土壤孔隙形状指数(F)的概念[21]。土壤孔隙的形状指数为孔隙等体积球体表面积与实际表面积之比,计算方法如下[22]:
| $ F = \frac{{{\text{π}}{d^2}}}{s} $ | (7) |
式中:d为孔隙的等效直径(μm);s为孔隙实际表面积(μm2)。F值越大,孔隙越接近球形。根据研究区域孔隙形状指数分布特点,结合孔隙形状外观特征(图 2B),本研究将孔隙按其形状指数大小分为3种类型:不规则孔隙(0 < F≤0.5)、规则孔隙(0.5 < F < 0.8)和近球形孔隙(0.8≤F < 1)。对土壤孔隙进行形状分类后,计算研究区域的不规则孔隙率、规则孔隙率和近球形孔隙率。
为分析不同直径雨滴击溅对土壤孔隙连通性的影响,一方面定量计算孤立孔隙率和连通孔隙率,另一方面根据孔隙网络模型分析连通孔隙的平均配位数、大孔平均配位数、平均孔喉半径和平均喉道长度,以表征土壤孔隙的连通度。如图 2C,假设一个孔隙网络由许多孔隙组成,识别孔隙网络中横截面积最小的部分作为孔隙之间的分界和孔隙网络模型中的孔喉,相连孔隙间的通道即为喉道。孔隙配位数为与孔隙相连接的喉道的数目,孔喉半径即孔喉的等面积圆半径,喉道长度即喉道连接的两个等效孔隙球体中心的直线距离。
采用Excel 2016进行数据整理与分析。数据统计分析均基于SPSS18.0软件,使用单因素方差分析(one-way ANOVA)和邓肯检验(Duncan’s test)对比一组或多组变量在P < 0.05显著水平上的差异;通过皮尔逊(Pearson)相关分析确定各结构参数和渗透系数在P < 0.05和P < 0.01显著水平上的相关性;基于主成分分析提取孔隙结构参数的主成分;使用回归分析进行各土壤结构参数与渗透系数关系曲线的拟合,以及土壤渗透系数与孔隙结构参数之间预测方程的建立。使用Origin Pro 2023进行图表绘制。
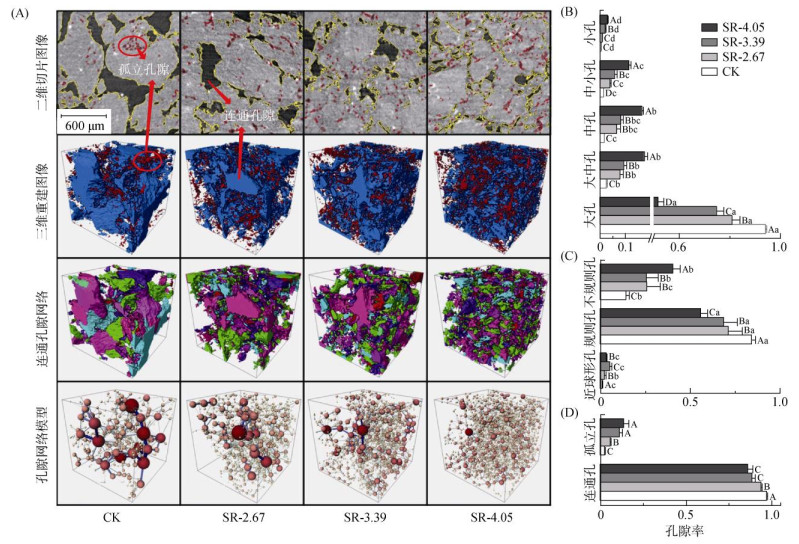
2 结果与分析 2.1 不同直径大小雨滴击溅对表土的影响 2.1.1 不同直径大小雨滴击溅对表土孔隙结构的影响表层土壤团聚体破碎程度随雨滴直径的增加逐渐增大,土壤孔隙被堵塞程度也更加严重。雨滴击溅后土壤孔隙数量较多,体积较小,孔隙分布趋于破碎化,导致孔隙连通性变差。在雨滴的压实与击溅剥离作用下,连通孔隙中大孔隙逐渐转变为小孔隙,喉道数量增多,土壤孔隙网络更为复杂(图 3A)。由表 2可知,雨滴击溅导致土壤总孔隙度显著降低,孔隙总数显著增多(P < 0.05)。2.67、3.39和4.05 mm直径雨滴击溅后土壤的总孔隙度分别降低了20.64%、36.05%和44.88%。较大雨滴直径(2.67和3.39 mm)使土壤孔隙平均等效直径显著减少(P < 0.05)。与对照组相比,雨滴击溅后土壤孔隙平均形状指数均有所减小,孔隙形状变得更不规则。通过分析4个处理下各类形状的孔隙率变化,发现大孔隙(等效直径 > 100 μm孔隙)、规则孔隙和连通孔隙的孔隙率随着雨滴直径的增大而减小(图 3B ~ 3D)。
|
(A:不同直径雨滴击溅下表土孔隙结构可视化;B ~ D:不同直径雨滴击溅下各类孔隙的孔隙率,不同大写字母表示同一孔隙类型在不同直径雨滴击溅处理间差异显著(P < 0.05),不同小写字母表示同一直径雨滴击溅处理下不同孔隙类型间差异显著(P < 0.05)) 图 3 不同直径大小雨滴击溅对表土孔隙结构的影响 Fig. 3 Effects of raindrop splashing with different diameters on topsoil pore structure |
连通孔隙网络模型配位数越小表示用于流体流动的通道越少,孔隙网络连通性越差。孔喉半径越小表示流体运动空间越狭窄,孔隙网络的连通性越差。喉道长度越短,表明流体在孔隙中传输的路径越短,孔隙网络的连通性越好。4.05 mm直径雨滴击溅后的连通孔隙配位数显著降低,雨滴击溅下土壤大孔隙配位数却显著增加(P < 0.05)(表 2),这说明雨滴击溅不仅导致土壤总孔隙度降低,还导致大多数较小孔隙的配位数降低,这意味着较小孔隙间的连接关系更不稳定,孔隙网络趋于脆弱化。孔喉半径和喉道长度随雨滴直径增加显著减小(P < 0.05),水流在相邻土壤孔隙间传输通道变窄,传输距离缩短,导致水分运输通道更加曲折。
2.1.2 不同直径大小雨滴击溅对表土渗透能力的影响与对照组土壤相比,3.39和4.05 mm直径雨滴击溅下土壤的初始入渗率和稳渗速率显著降低(P < 0.05),较小直径(2.67 mm)雨滴击溅下初始入渗率和稳渗速率没有显著变化(P > 0.05)(表 3)。4个处理下土壤的累计入渗量和渗透系数均存在显著差异(P < 0.05)。雨滴击溅对土壤渗透参数中的渗透系数影响程度最大,2.67、3.39和4.05 mm直径雨滴击溅土壤的渗透系数相较于对照组土壤分别降低了15.69%、40.42% 和71.77%。由以上分析可知,雨滴直径越大,雨滴动能对土壤的压实作用和对土壤团聚体的破坏和搬运作用越大。
|
|
表 3 不同直径大小雨滴击溅对土壤入渗参数的影响 Table 3 Effects of raindrop splashing with different diameters on topsoil infiltration parameters |
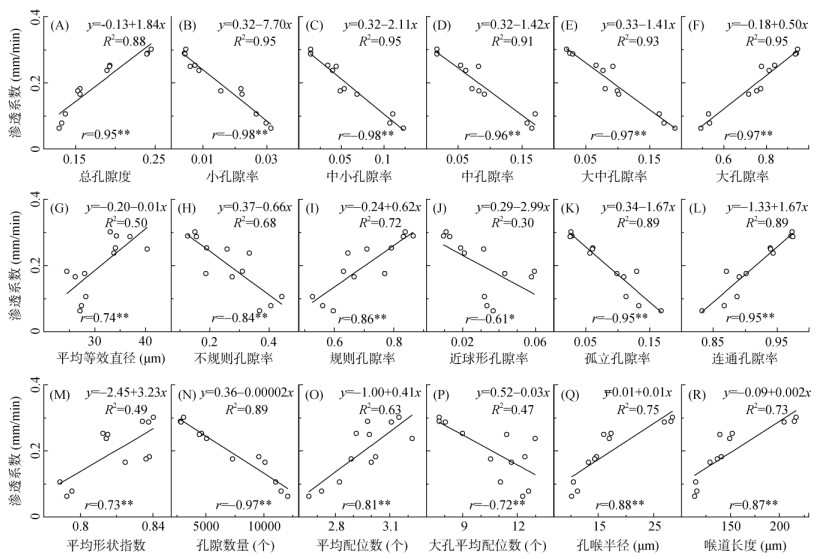
由图 4可知,土壤渗透系数与总孔隙度和平均等效直径呈显著的正相关关系,与孔隙总数呈显著的负相关关系(P < 0.01)。渗透系数与大孔隙率呈显著正相关关系(P < 0.01),相关系数约为0.97。渗透系数与等效直径小于100 μm孔隙的孔隙率呈显著的负相关关系(P < 0.01),相关性排序为:小孔隙率 > 中小孔隙率 > 大中孔隙率 > 中孔隙率。
|
(R2表示回归模型的调整后R2;r表示皮尔逊相关系数,*表示在P < 0.05水平上显著相关,**表示在P < 0.01水平上显著相关) 图 4 孔隙结构参数与渗透系数的回归分析 Fig. 4 Regression between pore structure parameters and saturated hydraulic conductivity |
土壤孔隙形状与渗透能力关系密切,土壤渗透系数与孔隙平均形状指数存在显著的正相关关系(P < 0.01)。土壤孔隙形状越不规则,土壤渗透系数越低,该结果表明规则的孔隙形状对土壤渗透有促进作用。从各形状类型孔隙的体积占比看,土壤渗透系数与规则孔隙率正相关,相关系数约为0.86,渗透系数与不规则孔隙率和近球形孔隙率负相关,相关系数分别约为–0.84和–0.61(图 4)。不规则孔隙不利于土壤渗透能力的提升,土壤中近球形孔隙通常为体积较小的孤立孔隙(图 3A),对水分运输的作用不大。因此,规则孔隙体积是影响土壤渗透能力的主要因素,规则孔隙是土壤水分传输的主要渠道。
土壤渗透系数与连通孔隙率显著正相关,与孤立孔隙率显著负相关。连通孔隙率是影响土壤渗透能力的主要因素。从孔隙网络模型相关参数的角度看,渗透系数与孔隙平均配位数、孔喉半径和喉道长呈显著的正相关关系(P < 0.01),相关性排序为:孔喉半径 > 喉道长度 > 平均配位数(图 4)。随着大孔平均配位数的增加,土壤渗透系数呈现降低趋势,但模型拟合效果较差(调整后R2 < 0.6)。孔隙整体的配位数越大,表明孔隙间的连通性越好,更有利于土壤水分入渗。土壤中大孔隙往往具有较大的配位数(表 2),这对土壤中水的多路径运移具有重要意义。然而,当大孔隙配位数较大时,会使水分运输途径更加曲折,导致入渗能力降低(图 4)。
2.3 基于主成分回归的土壤渗透能力预测以土壤渗透系数为因变量,综合考虑相关分析和各参数在预测土壤渗透能力时的现实意义,筛选出总孔隙度、大孔隙率、规则孔隙率、连通孔隙率和孔喉半径共5个自变量与土壤渗透系数进行回归分析。为避免变量之间的多重共线性对回归结果的干扰,同时保留原始数据中的大部分信息,提高回归模型的解释能力和预测精度,研究采用主成分回归方法建立自变量与渗透系数的回归模型。
首先对5个自变量进行主成分分析,KMO检验统计量的数值为0.802 > 0.7,且Bartlett检验的P值小于0.05,数据满足效度检验条件,适宜进行因子分析。
根据主成分分析结果,提取了一个主成分PC1,该主成分累积贡献率达到91.78%,对原始数据方差的解释程度较好(表 4)。最后,建立因变量渗透系数与主成分的线性回归方程,回归系数表如表 5所示,该模型具有统计学意义(P < 0.05),方程具有较高的拟合精度,预测效果较好(R2=0.93)。
|
|
表 4 总方差解释 Table 4 Total variance explanation |
|
|
表 5 土壤渗透系数与主成分回归系数表 Table 5 Soil saturated hydraulic conductivity and principal component regression coefficient |
将主成分与自变量进行多元线性回归,计算得到主成分与5个原始自变量的表达式:
| $ \begin{aligned} \mathrm{PCl} & =10.677 P_{\mathrm{T}}+2.773 P_{\mathrm{lp}}+3.746 P_{\mathrm{rp}}+9.308 P_{\mathrm{cp}} \\ & +0.067 R_{\mathrm{th}}-16.328 \end{aligned} $ | (8) |
将式(8)代入主成分与渗透系数的回归方程,得到渗透系数与土壤结构参数的关系模型:
| $ \begin{aligned} K & =0.402 T P+0.104 V_{l p}+0.1401 V_{r p}+0.350 V_{c p} \\ & +0.003 R_{t h}-0.415 \end{aligned} $ | (9) |
式中:K表示土壤渗透系数(mm/min);PT表示总孔隙度;Plp大孔隙率;Prp表示规则孔隙率;Pcp表示连通孔隙率;Rth表示孔喉半径(μm)。
3 讨论 3.1 雨滴击溅对表层土壤的影响本研究结果表明,雨滴击溅改变了土壤孔隙大小分布和形状。水蚀过程中土壤团聚体破碎的主要机制是快速湿润时的崩解和雨滴击溅导致的机械破碎[23]。随着雨滴直径、强度和能量的增加,团聚体颗粒分解,表层土壤形成更多的微团聚体颗粒[24]。因此,雨滴击溅后土壤小孔隙率增大,这与前人的研究结果一致[5]。本研究结果表明,雨滴击溅后土壤平均形状指数和规则孔隙率降低,不规则孔隙率增加,整体上土壤孔隙形状的规则性降低。然而,雨滴击溅前土壤近球形孔隙率(1.11%)却低于雨滴击溅后土壤近球形孔隙率(平均值为3.71%),这主要是由于部分不规则的孔隙在雨滴撞击的压实、分离和飞溅效应下被分解为较小的圆形孔隙[25]。
Zhang等[26]发现压实黄土具有更多的孤立孔隙。本研究结果表现出相似的规律:随着雨滴直径的增大,土壤孔隙中孤立孔隙呈增加趋势。相关研究表明,雨滴击溅后土壤中微团聚体数量增加,其形状较为规则和圆润,在水侵蚀过程中更容易悬浮和运移[6]。该发现揭示了雨滴击溅后土壤中孤立孔隙增多的原因:一方面,雨滴打击使土壤团聚体破碎,这些破碎的团聚体之间可能会形成新的与外界不连通的小孔隙或裂隙;另一方面,雨滴打击导致连通孔隙被微团聚体堵塞,产生了更多的孤立孔隙。
雨滴击溅可以降低土壤的入渗能力,这与前人的研究结果一致[9-10]。造成土壤入渗率下降的主要原因是雨滴击溅导致团聚体破碎成微团聚体,破坏了表层土壤的团聚体结构[17]。除雨滴直径外,土壤入渗能力还受降雨次数、土壤类型和耕作方式等多方面因素影响。例如,Ma等[20]发现土壤稳定入渗速率随雨滴击溅次数的增加而减小,并且土壤达到稳定入渗状态的时间随着雨滴击溅次数的增加逐渐提前;陈娟等[27]通过对比不同土壤类型入渗特征的差异,发现风沙土的入渗性能最好,基岩风化残积土次之,灰钙土入渗性能最差,不同土壤结构的差异是造成这种现象的主要原因;周宾和胡树文[28]发现随着种植年限的增加,土壤入渗性能变化明显。后续应加强对这些方面的研究。
3.2 土壤结构与入渗能力的关系渗透系数被认为是决定土壤入渗速率、渗滤深度和其他水文过程的关键土壤物理变量[29]。本研究将土壤孔隙参数作为自变量,土壤渗透系数作为因变量,分析了各孔隙结构参数与土壤渗透能力的相关性,结果表明,较大的孔隙体积和等效直径可以为水分运输提供更大的空间和通道,提高水分的运输效率,对土壤入渗能力具有促进作用,其中大孔隙率是影响土壤入渗能力的主要因素。有研究显示,入渗到土壤中的水分几乎都是通过大孔和中孔传输[30];土壤大孔隙率的降低会减少土壤水分的主要运输通道,从而降低土壤渗透率[31]。
Yang等[5]的研究表明细长孔隙(F < 0.2)对水分在土壤孔隙中的传输起主要作用。该结论与本研究结果不一致,主要是由于其将连通孔隙团簇作为一个整体进行形状指数计算。连通孔隙团簇具有体积大、形状不规则的特点(图 3A)。经计算,本研究数据中连通孔隙团簇的形状指数均小于0.2。本研究引入了连通孔隙网络的概念,将连通孔隙团簇分割后对全部孔隙的形状与渗透能力的关系展开分析,避免了较大连通孔隙团簇体积对孔隙形状分析结果的影响。本研究结果表明,规则孔隙是影响土壤渗透能力的主要因素。土壤孔隙形态越趋近于圆形,渗透系数越大[32]。形状不规则的孔隙可能会增加水分在孔隙中发生滞留或逆渗现象,导致土壤水分的传输受到阻碍。
孤立孔隙和连通孔隙是衡量土壤孔隙连通性的重要指标,二者在土壤水分运移中发挥着不同的作用[33]。本研究定量分析了孤立孔隙率和连通孔隙率对土壤入渗能力的影响,发现连通孔隙对土壤渗透能力具有促进作用,这与前人的研究结果一致[34]。在此基础上,本研究定量分析了各连通孔隙网络模型参数对渗透能力的影响,结果表明,孔隙网络模型参数中孔喉半径对渗透系数的影响最大(图 4),该结果进一步支持了前人的研究成果:土壤中喉道半径对控制水分流动起主要作用,大喉道的作用高于多个小喉道的叠加效果[15]。
4 结论雨滴击溅通过改变土壤孔隙的大小、形状和连通状况对土壤的入渗能力造成影响。孔隙大小方面,土壤大孔隙率与土壤渗透系数正相关(P < 0.01),相关系数为0.97。较大的孔隙体积可以为水分运输提供更大的空间和通道,提高水分的运输效率;孔隙形状方面,规则孔隙率与土壤渗透系数正相关(P < 0.01),相关系数约为0.86,表明规则孔隙是土壤水分传输的主要渠道;孔隙连通性方面,土壤连通孔隙率和孔喉半径对渗透系数的影响程度最大(P < 0.01),相关系数分别为0.95和0.88,表明土壤中连通孔隙及其喉道半径对控制水分流动起主要作用。土壤孔隙微观结构对渗透能力的影响是一个综合性的过程,较大的孔隙能够提供更多的通道,孔隙形状的规则性和孔隙连通性决定了水分在土壤中的流动和分布方式。
| [1] |
Fu Y, Li G L, Zheng T H, et al. Fragmentation of soil aggregates induced by secondary raindrop splash erosion[J]. CATENA, 2020, 185: 104342 DOI:10.1016/j.catena.2019.104342 (  0) 0) |
| [2] |
李光录, 吴发启, 庞小明, 等. 泥沙输移与坡面降雨和径流能量的关系[J]. 水科学进展, 2008, 19(6): 868-874 DOI:10.3321/j.issn:1001-6791.2008.06.017 (  0) 0) |
| [3] |
Rabbi S M F, Tighe M K, Flavel R J, et al. Plant roots redesign the rhizosphere to alter the three-dimensional physical architecture and water dynamics[J]. New Phytologist, 2018, 219(2): 542-550 DOI:10.1111/nph.15213 (  0) 0) |
| [4] |
李禹凝, 王金满, 张雅馥, 等. 干旱半干旱煤矿区土壤水分研究进展[J]. 土壤, 2023, 55(3): 494-502 DOI:10.13758/j.cnki.tr.2023.03.005 (  0) 0) |
| [5] |
Yang M X, Fu Y, Li G L, et al. Microcharacteristics of soil pores after raindrop action[J]. Soil Science Society of America Journal, 2020, 84(5): 1693-1704 DOI:10.1002/saj2.20113 (  0) 0) |
| [6] |
Li G L, Fu Y, Li B Q, et al. Micro-characteristics of soil aggregate breakdown under raindrop action[J]. CATENA, 2018, 162: 354-359 DOI:10.1016/j.catena.2017.10.027 (  0) 0) |
| [7] |
付玉, 李光录, 郑腾辉, 等. 雨滴击溅对耕作层土壤团聚体粒径分布的影响[J]. 农业工程学报, 2017, 33(3): 155-160 (  0) 0) |
| [8] |
Fox D M, Darboux F, Carrega P. Effects of fire-induced water repellency on soil aggregate stability, splash erosion, and saturated hydraulic conductivity for different size fractions[J]. Hydrological Processes, 2007, 21(17): 2377-2384 DOI:10.1002/hyp.6758 (  0) 0) |
| [9] |
Carmi G, Abudi I, Berliner P. An experimental study to assess the effect of the energy and the electrolyte concentration of rain drops on the infiltration properties of naturally crusted soils[J]. Journal of Arid Environments, 2018, 152: 69-74 DOI:10.1016/j.jaridenv.2018.01.009 (  0) 0) |
| [10] |
Liu H, Lei T W, Zhao J, et al. Effects of rainfall intensity and antecedent soil water content on soil infiltrability under rainfall conditions using the Run off-on-out method[J]. Journal of Hydrology, 2011, 396(1/2): 24-32 (  0) 0) |
| [11] |
Basset C, Abou Najm M, Ghezzehei T, et al. How does soil structure affect water infiltration? A meta-data systematic review[J]. Soil and Tillage Research, 2023, 226: 105577 DOI:10.1016/j.still.2022.105577 (  0) 0) |
| [12] |
张靖, 陈琳, 周虎, 等. 基于数字图像技术的土壤孔隙结构定量研究进展[J]. 土壤, 2023, 55(1): 21-29 DOI:10.13758/j.cnki.tr.2023.01.003 (  0) 0) |
| [13] |
Rabot E, Wiesmeier M, Schlüter S, et al. Soil structure as an indicator of soil functions: A review[J]. Geoderma, 2018, 314: 122-137 DOI:10.1016/j.geoderma.2017.11.009 (  0) 0) |
| [14] |
胡黎明, 林丹彤, 张鹏伟, 等. 多孔介质孔隙结构模型及其在渗流分析中的应用[J]. 太原理工大学学报, 2022, 53(3): 360-370 (  0) 0) |
| [15] |
Wei T T, Fan W, Yuan W N, et al. Three-dimensional pore network characterization of loess and paleosol stratigraphy from South Jingyang Plateau, China[J]. Environmental Earth Sciences, 2019, 78(11): 333 DOI:10.1007/s12665-019-8331-z (  0) 0) |
| [16] |
Yu X L, Lu S G. Reconfiguration of macropore networks in a silty loam soil following biochar addition identified by X-ray microtomography and network analyses[J]. European Journal of Soil Science, 2019, 70(3): 591-603 DOI:10.1111/ejss.12773 (  0) 0) |
| [17] |
Fu Y, Li G L, Zheng T H, et al. Splash detachment and transport of loess aggregate fragments by raindrop action[J]. CATENA, 2017, 150: 154-160 DOI:10.1016/j.catena.2016.11.021 (  0) 0) |
| [18] |
伍石生, 戴经梁, 彭波. 压实黄土的微结构及其渗水的研究[J]. 西安公路交通大学学报, 1998, 18(4): 17-20 (  0) 0) |
| [19] |
Houston A N, Otten W, Falconer R, et al. Quantification of the pore size distribution of soils: Assessment of existing software using tomographic and synthetic 3D images[J]. Geoderma, 2017, 299: 73-82 DOI:10.1016/j.geoderma.2017.03.025 (  0) 0) |
| [20] |
Ma G G, Li G L, Mu X D, et al. Effect of raindrop splashes on topsoil structure and infiltration characteristics[J]. CATENA, 2022, 212: 106040 (  0) 0) |
| [21] |
Wadell H. Volume, shape, and roundness of rock particles[J]. The Journal of Geology, 1932, 40(5): 443-451 (  0) 0) |
| [22] |
Xuan K F, Li X P, Yu X L, et al. Effects of different organic amendments on soil pore structure acquired by three-dimensional investigation[J]. European Journal of Soil Science, 2022, 73(4): e13264 (  0) 0) |
| [23] |
Shi Z H, Yan F L, Li L, et al. Interrill erosion from disturbed and undisturbed samples in relation to topsoil aggregate stability in red soils from subtropical China[J]. CATENA, 2010, 81(3): 240-248 (  0) 0) |
| [24] |
Fu Y, Li G L, Wang D, et al. Raindrop energy impact on the distribution characteristics of splash aggregates of cultivated dark loessial cores[J]. Water, 2019, 11(7): 1514 (  0) 0) |
| [25] |
Dalla Rosa J, Cooper M, Darboux F, et al. Influence of crust formation on soil porosity under tillage systems and simulated rainfall[J]. Hydrology, 2017, 4(1): 3 (  0) 0) |
| [26] |
Zhang L X, Qi S W, Ma L N, et al. Three-dimensional pore characterization of intact loess and compacted loess with micron scale computed tomography and mercury intrusion porosimetry[J]. Scientific Reports, 2020, 10(1): 8511 (  0) 0) |
| [27] |
陈娟, 陈林, 宋乃平, 等. 荒漠草原不同土壤类型水分入渗特征[J]. 水土保持学报, 2018, 32(4): 18-23 (  0) 0) |
| [28] |
周宾, 胡树文. 不同种稻年限对苏打盐碱土孔隙和入渗性能的影响[J]. 土壤学报, 2023, 60(1): 99-105 (  0) 0) |
| [29] |
Jafari R, Sheikh V, Hossein-Alizadeh M, et al. Effect of soil sample size on saturated soil hydraulic conductivity[J]. Communications in Soil Science and Plant Analysis, 2017, 48(8): 908-919 (  0) 0) |
| [30] |
贾昂元, 张勇勇, 赵文智, 等. 干旱区绿洲农田土壤大孔隙与水分入渗特征[J]. 土壤学报, 2022, 59(2): 486-497 (  0) 0) |
| [31] |
Dal Ferro N, Charrier P, Morari F. Dual-scale micro-CT assessment of soil structure in a long-term fertilization experiment[J]. Geoderma, 2013, 204/205: 84-93 (  0) 0) |
| [32] |
包含, 尹晓晴, 兰恒星, 等. 基于微结构量化的含渐变带天然黄土渗透各向异性研究——以延安新区Q1黄土为例[J]. 岩土工程学报, 2023, 45(4): 730-738 (  0) 0) |
| [33] |
房营光, 陈建, 谷任国, 等. 基于有效比表面积修正的Kozeny-Carman方程在黏土渗透中的适用性研究[J]. 岩土力学, 2020, 41(8): 2547-2554 (  0) 0) |
| [34] |
Wen T D, Chen X S, Shao L T. Effect of multiple wetting and drying cycles on the macropore structure of granite residual soil[J]. Journal of Hydrology, 2022, 614: 128583 (  0) 0) |
2. Institute of Soil Water Conservation, Northwest A & F University, Yangling, Shaanxi 712100, China
 2024, Vol. 56
2024, Vol. 56


