2. 安庆师范大学资源环境学院, 安徽安庆 246133
土壤是维持生态系统平衡与稳定的最主要媒介。矿山在开采、选矿、冶炼过程中产生的废弃物不仅污染企业用地,而且对周边耕地土壤带来生态风险[1]。矿区土壤重金属污染具有高含量、空间异质性、伴生性等特征,在直接暴露或食物链途径等作用下,易对生态系统和人体健康产生潜在危害[2-3]。
传统的土壤重金属空间分布研究是通过实地调查、采样和测试获取不同采样点的土壤重金属含量来分析。由于采样条件、研究区实际情况和研究成本等因素的限制,大量进行采样、测试分析并不现实。因此运用合理方法,通过样点数据预测掌握整个研究区土壤重金属空间分布具有重要意义。
利用已知点的数据对未知点重金属元素含量进行空间插值可以快速得到整个研究区域的重金属分布状况。目前空间插值的方法主要有确定性插值方法,如反比距离权重法(Inverse distance weighting,IDW)、径向基函数(Radial basis function,RBF)、全局多项式插值(Global polynomial interpolation,GPI)等和地统计插值方法(如克里金法)两类[4]。曾星等[5]和张龙等[6]分别采用IDW方法和结合环境因子的克里金法对农田土壤指标的空间分布进行了分析。总体来看,确定性插值方法计算效率高,对于数据量充足且均匀分布的样本点,插值结果一般较为平滑,但对于非均匀分布的点,插值结果可能不够准确。地统计插值方法能够考虑空间数据的统计特性,更好地反映数据的空间变异性,提供插值结果的不确定性评估。但两种方法对于边界问题和异常值处理比较复杂,可能无法进行准确的插值[7]。
近年来,机器学习算法凭借其计算速度快与准确度高的特点,在土壤重金属污染状况评估、土壤重金属元素含量预测方面得到了广泛应用[8]。由于土壤是一个空间连续性变异的非均质体,各样点的重金属含量与其所在点位置和污染等级之间存在复杂的随机非线性映射关系[9]。人工神经网络(Artificial neural network,ANN)是一种仿生机制数学模型,能模仿动物神经连接节点分布式并行处理信息的行为[10]。ANN能较好地映射样点重金属含量与其空间位置的非线性关系,提供一批相互对应的输入和输出数据,分析其内在联系并预先设计预测模式,输入新数据即可推算输出结果,使得ANN能够对空间各点处的土壤重金属含量进行预测和评价[11]。
BP神经网络(Back propagation neural network,BPNN)模型建立过程需要大量训练样本进行学习,并使用测试样本进行验证。然而由于客观条件限制,有时很难获取足够的样本数据。样本数据不足可能会影响模型的准确性和可靠性。因此,在实际应用中,需要寻找其他有效方法来解决样本数据不足的问题,例如采用数据增强技术、合理选择特征等。Wang等[12]针对小样本数据进行表层土壤湿度反演存在的过拟合和目标任务欠拟合的问题,提出利用alpha近似方法对实测表层土壤湿度数据进行扩充,为机器学习模型提供更多的训练数据。尹光彩等[13-14]利用遗传算法(Genetic algorithm,GA)耦合ANN产生新个体实现空间插值,模型具有良好的预测性能,但其产生的位置具有随机性。戴倩倩等[15]和龚仓等[16]通过研究和收集关于地理探测器在土壤重金属空间分异领域的研究,发现高程差异对土壤pH和重金属空间分布和含量有显著影响。高程会影响土壤的湿度、类型、植被覆盖和雨水淋溶等,从而影响土壤重金属空间分布和含量。目前大多数关于GA和BPNN结合的研究只是利用GA可以收敛到全局最优解,来提高神经网络收敛速度、全局优化能力和学习能力。然而利用GA对小样本数据进行数据扩增,再耦合BPNN,结合平面坐标与高程因素对指定点来进行预测插值方面的研究鲜有报道。
因此,本研究在前人研究的基础上,提出了基于GA和BPNN的复合模型——GABP。以安徽省池州市某矿区及其周边为研究区,首先利用GA对土壤采样点数据进行扩增,然后用遗传算法优化的BP评价网络(Genetic algorithm-BP evaluation network,GA-EN)对新个体数据进行评价;最后,使用遗传算法优化的BP预测网络(Genetic algorithm-BP prediction network,GA-PN)对研究区土壤pH和重金属含量空间分布进行预测,并与传统的IDW法进行对比。该模型不仅考虑采样点的地理位置,还考虑了高程对土壤重金属分布和含量的影响,数据扩增部分考虑了元素间的伴生性,克服了BP神经网络和传统插值方法需要大量数据及传统插值方法边界无法准确插值、出现负值的缺陷,使模型预测结果有较高的准确性与稳定性。研究方法为区域土壤重金属元素含量空间分布预测提供了一种新的参考。
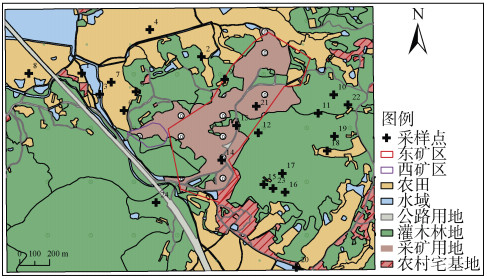
1 材料与方法 1.1 研究区概况与采样点布置本文以安徽省池州市“某矿区及周边区域土壤环境现状调查”项目数据为依托开展研究。该矿区位于长江中下游南岸、皖南山区北。原矿山地下分为东西两个开采区,东矿区为硫铁矿,西矿区为金矿。现西矿区已停止开采,研究区包含矿区和居民区、农田等,总面积为4.42 km2(图 1)。分别于2020年11—12月和2021年11月在研究区进行布点采样。以国家场地调查和场地环境监测的相关技术导则要求为前提,结合前期踏勘与资料分析结果,对开采区及周边敏感目标土壤污染情况进行调查;以东矿区周边1 km为监测区域,参照监测区域用地类型、淋溶水流向等进行布点;基于二分法原理对监测半径进行划分,在矿区排污口下游、贫液池上下游和矿区排污口等有污染源的地区加密布点;确保采样点的布置能够满足判别矿区及周边地块污染情况的要求,同时在现场环境条件不具备采样条件时,对点位进行调整,做到现场勘察与采样相结合[17],确定新的采样点位,用GPS记录坐标。鉴于前期调查发现西部地区整体地势较高,未受到本次项目区内淋溶水等污染的影响,因此在该区域未设置采样点。最终共采集表层(0 ~ 20 cm)土壤样品24份,点位分布见图 1。
|
图 1 研究区位置及采样点示意图 Fig. 1 Location and sampling points in study area |
pH采用pH计玻璃电极法测定,Cd、Pb采用石墨炉原子吸收分光光度法测定,Cr、Cu、Ni采用火焰原子吸收分光光度法测定,Hg、As采用原子荧光法测定,检测结果见表 1。数字高程数据采用的是GDEMV3 30M,精度为30 m,下载自地理空间数据云网站(https://www.gscloud.cn/)。
|
|
表 1 土壤pH和重金属含量(mg/kg) Table 1 Soil pH and heavy metal contents |
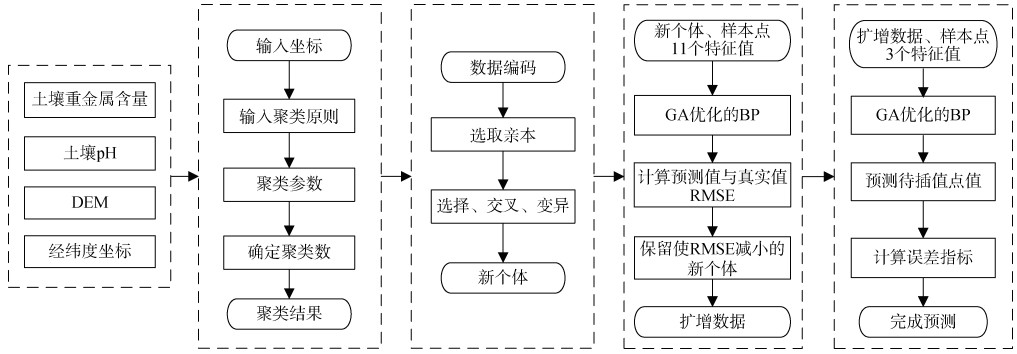
本研究主要基于GA和BPNN,构建了一种预测土壤pH和重金属含量空间分布的复合模型——GABP。模型预测的具体流程(图 2)为:①使用K–均值聚类算法,根据采样点坐标计算距离,对24个采样点进行分类,再利用GA的繁殖机制,生成一系列待检验的新个体;②将新个体同样本数据一同作为训练集输入到GA-EN中,样本点的11个已知特征值作为输入,预测值作为输出,计算样本点预测值和真实值之间的均方根误差(RMSE);③重复前面两步,仅保留加入训练集后,计算的RMSE不比上一轮的值大的新个体,确保只保留对模型预测精度提升有贡献的个体;④达到迭代次数后,输出所有保留的新个体,完成数据扩增;⑤构建GA-PN网络,将扩增后的数据和样本数据作为新的数据集,训练GA-PN,预测研究区内待求点的含量值。
|
图 2 GABP模型设计流程图 Fig. 2 GABP model design workflow diagram |
K–均值聚类是一种基于距离度量的无监督学习方法,用于将一个数据集分成k个不同的组或类。其主要思想是找到一些中心点,将每个点分配给离它最近的中心点所对应的类[18]。本研究中两点间的距离采用欧氏距离,种群中心Ci的横坐标用公式(1)计算。聚类的类别数k依据下面3个指标选取:①每个类内部采样点地理位置的标准差(Average within cluster std,AWCS)尽量小;②不同类之间采样点地理位置的标准差(Between-cluster std,BCS)尽量大;③每个类内采样点数量(Average cluster size,ACS)尽量多[14]。相关计算公式如下:
| $ {C_{ix}} = \frac{{\sum\limits_{i = 1}^n {Xi} }}{n} $ | (1) |
| $ {\text{Std = }}\sqrt {\frac{{\sum\limits_{i = 1}^n {{{({X_i} - \overline X )}^2}} }}{n}} \text{,} {\text{AWCS}} = \frac{{\sum\limits_{i = 1}^k {{\text{Std}}i} }}{k} $ | (2) |
| $ {\text{BCS}} = \sqrt {\frac{{\sum\limits_{i = 1}^k {{{(Ci - \bar C)}^2}} }}{k}} $ | (3) |
| $ {\text{ACS}} = \frac{N}{k} $ | (4) |
式中:Cix代表种群Ci的新中心点的横坐标,n是每个种群内点的数量,Xi 是种群Ci中的第i个点的横坐标,
GA是一种随机搜索最优解的智能算法,模拟了生物种群中个体优胜劣汰的自然规律[5]。它以目标问题的不同解作为不同的个体生成种群,然后对种群进行选择、交叉、变异来寻求最优个体以实现对目标问题的求解[19]。为了使GA可以更加有效地搜索适应度函数的最优解空间,且避免出现异常值,在算法中设置新个体的上界为种群内各元素对应的最大值,下界为种群内各元素对应的最小值。
1.3.3 BP神经网络(Back propagation neural network,BPNN)BPNN是一种非线性模型,它以数据驱动的方式进行建模和预测,可以避免人为设置权重的影响[20],具有强大的拟合能力,能够处理多变量输入以及非参数建模等优点。土壤中重金属元素含量通常受多个因素的影响,如土壤性质和人为活动等,这些因素之间的关系是非线性的,BPNN可以同时将它们作为输入变量,从而更全面地预测土壤中重金属含量。本研究分别构建GA-EN和GA-PN两种不同结构和功能的BPNN。
1) GA-EN评价网络。GA-EN的作用是在遗传算法每一轮产生新个体后计算新个体RMSE,决定其是否保留。合理设计BPNN结构可以使其具有较好的泛化能力,该神经网络结构(图 3)为:输入层和输出层各11个神经元,代表采样点的11个特征值;2个隐含层采用sigmoid函数;输出层采用的是正线性激活函数Poslin,在输入值不小于0时,输出值与输入相同,在输入值小于0时,输出0。在模型中,先将GA产生的新个体添加到数据集中,形成新的数据集;然后训练GA-EN,用GA-EN进行预测,得到预测结果;计算RMSE并根据其大小取舍新个体。

|
图 3 GA-EN网络结构 Fig. 3 GA-EN network architecture |
2) GA-PN预测网络。在训练集中,GA-PN模型采用k折交叉验证法来选择神经网络的参数,本研究采用了8折交叉验证(k=8)。通过这种方式,可以更准确地评估模型的性能,选择较好的参数组合。GA-PN模型基于前期数据扩增结果构建,用于预测研究区内其他位置土壤pH和重金属元素含量。该神经网络结构(图 4)为:输入层3个神经元,分别表示待预测点位的经度、纬度、高程;3个隐含层采用sigmoid函数;输出层1个神经元,表示预测点的某一种元素含量的预测值。

|
图 4 GA-PN网络结构 Fig. 4 GA-PN network architecture |
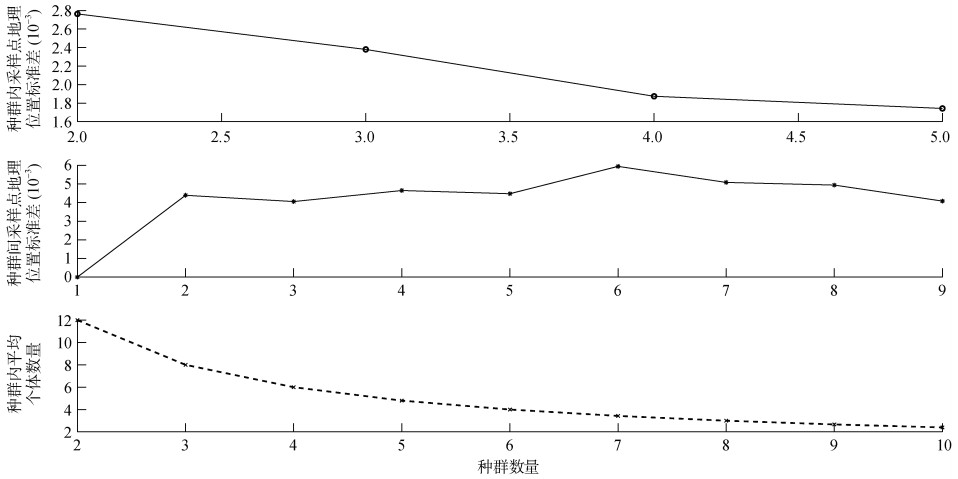
随着种群数量逐渐增加,观察到3个指标的变化逐渐减小或趋于稳定(图 5)。得出以下结论:当k=5,①种群内标准差逐渐减小;②种群间标准差逐渐增大;③种群内平均个体数量趋于稳定。因此,可以认为当k=5时,聚类效果最佳。
|
图 5 K–均值聚类指标折线 Fig. 5 Line plot of K–means clustering metrics |
在初始样本数据构成的5个种群内分别使用GA进化繁衍,再对新个体用GA-EN进行评价。最终,样本点的数量从24个扩增到5 019个,满足BPNN需要大量样本数据的要求。
2.1.3 GABP模型预测GABP模型对pH和7种重金属的含量及分布进行了预测,模型的均方根误差RMSE、决定系数R2、相关系数r和平均绝对误差MAE见表 2。
|
|
表 2 三种模型精度评价 Table 2 Accuracy evaluation of three model |
表 2为3种模型交叉验证的参数值。结果显示GABP模型在预测pH和7种土壤重金属元素含量方面表现出了相对较好的精度和拟合效果。按照R2从大到小进行排序,可以看出:Hg最高,其余依次是Pb、Cr、Cu、pH、Cd、As和Ni。GABP相较于BP网络和IDW而言,除Cr外,对所有特征预测的R2和r均有明显提升,且RMSE和MAE较小,表明较少样本经过GA数据扩增后,训练出的模型能够较好地解释数据变异,预测结果与实际值拟合程度较好,准确度明显提升。
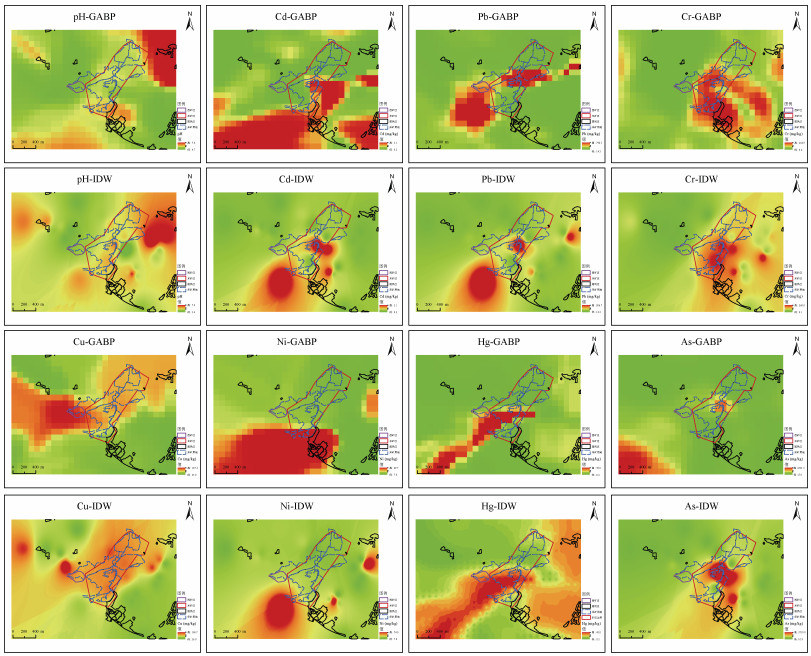
2.2 GABP模型与IDW预测方法的对比 2.2.1 两种方法空间分布预测结果对比使用ArcGIS软件将预测值和矢量网格单元进行关联,再赋值和显示后,得到GABP空间分布预测结果,并将其与IDW空间插值结果进行对比。图 6为GABP和IDW预测结果。
|
图 6 GABP与IDW预测结果 Fig. 6 GABP and IDW prediction results |
图 6表明,GABP复合模型预测结果与IDW插值结果在空间分布上总体上保持一致。特别是Hg、Cu和pH的空间分布与IDW结果非常接近,高值区和低值区的分布位置基本一致。其中,两种方法预测的Cd、Pb、As元素的高值区都分布在采矿用地的西南部,原因为研究区东矿区为硫铁矿,西矿区为废弃金矿,研究区外西南部存在一处金矿。而硫铁矿和金矿中都可能含有一定量的Cd、Pb、As,在开采加工过程中可能导致其释放到土壤中,因此这些区域出现高值。Cr元素高值区主要分布在东矿区南部和研究区东部。Ni元素的高值区主要在研究区的西南部,东部有一小范围高值区。Cu元素从西部的高值区开始沿着东矿区逐渐降低直至研究区东北部。硫铁矿的形成除了与S、Fe成矿元素供给与沉积密切相关外,通常还会伴生如Cu等元素,矿山开采容易导致这些元素在土壤中累积。Hg元素含量的高值区域都显示为一部分从研究区中部沿西南方向延伸,另一部分在研究区东部,两种方法预测的Hg最大值最小值区间完全一致,预测效果最佳,与精度评价的结果相同。两种方法预测pH的空间分布也基本一致,GABP预测的结果相对更连续,而IDW预测结果显示研究区内重金属含量比较复杂,高值和低值区域相互交错,细节表现更好。
2.2.2 GABP模型优越性GABP模型相较于传统的BPNN和常规IDW法具有以下优势:
1) 利用GA进行数据扩增,大幅增加了样本数据量,提高了模型的泛化能力,改善了模型的稳定性,减少了误差。从交叉验证的结果可以看出,GABP模型的R2和r明显高于其他两种方法,RMSE和MAE值也相对较低,表明其优于其他两种方法。
2) 在GA内部设置新个体特征值的上下限来确保不会出现异常值,并在BPNN输出层采用Poslin函数,确保插值结果不会出现负值。从图 6可以看出,GABP预测的每一特征值均在IDW预测区间内,解决了一些插值方法边界可能出现负值的情况。
3) 模型不仅考虑了平面地理位置,还综合考虑了高程因素,提高了非线性预测能力,使得结果更加准确。
4) 从图 6中看出,在预测极大值与极小值时,GABP虽然没有IDW边缘光滑,但其不会有明显的牛眼效应。
3 结论1) 研究区土壤pH和7种重金属的分布趋势基本一致,高值区主要出现在研究区的西南部和东部,呈现出显著的空间分异性。
2) 相较于传统的BPNN和IDW,GABP具有较高的决定系数和较低的误差,表明该模型弥补了传统方法需要大量实测样本数据支撑训练的缺点。与IDW法相比,模型的预测结果与其基本一致,说明GABP模型是可靠的。
3) 模型不仅考虑了经纬度,还考虑了高程因素,模型对pH和7种重金属含量具有较好的预测结果,表明该模型在小尺度区域土壤重金属含量空间分布预测是可行的。
本文的研究方法对改进传统的空间预测方法和土壤重金属、水分等预测提供了新思路,对土壤环境评价具有参考意义。本文在预测部分考虑了地理位置和高程属性,但土壤重金属元素可能还受元素间伴生性、土地利用类型等因素的影响。因此,后续研究可以综合考虑这些因素,对输入特征进行优化。
致谢: 感谢广东工业大学尹光彩老师为本研究提供的帮助!
| [1] |
Zhang Y M, Li S, Chen Z, et al. A systemic ecological risk assessment based on spatial distribution and source apportionment in the abandoned lead acid battery plant zone, China[J]. Journal of Hazardous Materials, 2018, 354: 170-179 DOI:10.1016/j.jhazmat.2018.04.054 (  0) 0) |
| [2] |
Liu M, Zhang A B, Liao Y J, et al. The environment quality of heavy metals in sediments from the central Bohai Sea[J]. Marine Pollution Bulletin, 2015, 100(1): 534-543 DOI:10.1016/j.marpolbul.2015.09.001 (  0) 0) |
| [3] |
成晓梦, 孙彬彬, 吴超, 等. 浙中典型硫铁矿区农田土壤重金属含量特征及健康风险[J]. 环境科学, 2022, 43(1): 442-453 (  0) 0) |
| [4] |
汤国安, 杨昕. ArcGIS地理信息系统空间分析实验教程(2版)[M].
科学出版社, 北京, 2012
(  0) 0) |
| [5] |
曾星, 张华. 基于GIS的碧流河上游农田土壤性状空间分布特征[J]. 土壤, 2023, 55(6): 1354-1362 (  0) 0) |
| [6] |
张龙, 张忠启, 蔡何青, 等. 贵州毕节植烟区土壤pH空间分布特征及对施肥的影响[J]. 土壤, 2023, 55(1): 85-93 (  0) 0) |
| [7] |
尹光彩, 陶琳, 陈幸玲, 等. 一种耦合遗传算法和神经网络的土壤污染物含量插值方法: CN113159219B[P]. 2022-04-08.
(  0) 0) |
| [8] |
何云山. 区域土壤重金属污染预测模型研究与应用[D]. 北京: 北京信息科技大学, 2021.
(  0) 0) |
| [9] |
胡大伟, 卞新民, 许泉. 基于ANN的土壤重金属分布和污染评价研究[J]. 长江流域资源与环境, 2006, 15(4): 475-479 (  0) 0) |
| [10] |
谢虹. 农田土壤重金属污染评价常用研究方法[J]. 山东化工, 2018, 47(10): 194–195, 200 (  0) 0) |
| [11] |
陈晓燕, 范成五, 瞿飞, 等. 土壤重金属污染评价方法概述[J]. 浙江农业科学, 2017, 58(10): 1801–1804, 1810 (  0) 0) |
| [12] |
Wang Y L, Zhao J H, Guo Z W, et al. Soil moisture inversion based on data augmentation method using multi- source remote sensing data[J]. Remote Sensing, 2023, 15(7): 1899 DOI:10.3390/rs15071899 (  0) 0) |
| [13] |
尹光彩, 宋小旺, 陶琳, 等. 一种基于遗传算法的土壤重金属含量空间插值方法: CN111209679B[P]. 2023.09. 29.
(  0) 0) |
| [14] |
Yin G C, Chen X L, Zhu H H, et al. A novel interpolation method to predict soil heavy metals based on a genetic algorithm and neural network model[J]. The Science of the Total Environment, 2022, 825: 153948 DOI:10.1016/j.scitotenv.2022.153948 (  0) 0) |
| [15] |
戴倩倩, 徐梦洁, 庄舜尧, 等. 基于地理探测器的封丘县农田土壤重金属分布影响因素研究[J]. 土壤, 2022, 54(3): 564-571 (  0) 0) |
| [16] |
龚仓, 王顺祥, 陆海川, 等. 基于地理探测器的土壤重金属空间分异及其影响因素分析研究进展[J]. 环境科学, 2023, 44(5): 2799-2816 (  0) 0) |
| [17] |
谢芳, 黄海英. 重污染地区土壤调查点位布设方法[J]. 科技资讯, 2010, 8(23): 164 (  0) 0) |
| [18] |
王政. 基于贝叶斯地统计学方法的区域土壤重金属空间预测研究[D]. 济南: 山东师范大学, 2022.
(  0) 0) |
| [19] |
曹文琪, 张聪. 深度复合模型下的土壤重金属含量预测[J]. 计算机工程与设计, 2021, 42(4): 1128-1134 (  0) 0) |
| [20] |
李向, 管涛, 徐清. 基于BP神经网络的土壤重金属污染评价方法——以包头土壤环境质量评价为例[J]. 中国农学通报, 2012, 28(2): 250-256 (  0) 0) |
2. School of Resources and Environment, Anqing Normal University, Anqing, Anhui 246133, China
 2024, Vol. 56
2024, Vol. 56


