土壤有机碳(SOC)是衡量土壤肥力的关键指标,估算SOC对促进耕地可持续利用和实现作物高产稳产具有重要意义。传统SOC估算主要通过地球化学方法[1],结果准确可靠,但存在投入高、周期长及破坏土壤环境等问题。有学者利用地面高光谱数据构建SOC反演模型,得出SOC含量与可见光和短波红外光谱指数呈显著相关[2-3],实现了SOC快速估算,既降低了成本,又保证了土壤环境完整性,但上述研究无法反映区域尺度上SOC的空间变异特征。GIS及地统计学的结合解决了区域SOC估算问题,使得平原、丘陵等不同地貌的SOC空间变异得以估算[4-5],但该方法对样本数量要求高,无法全面揭示环境因子对SOC的影响,在表达SOC空间格局细节方面仍有待提高。卫星遥感技术以其高时空分辨率、易于获取等优势,为SOC快速估算及变化监测开辟了新的途径。基于MODIS数据的研究得出,中国东北部、西南部以及东南部SOC含量高,而西北部SOC含量低[6],但其250 m的空间分辨率限制了其在中小尺度SOC估算中的应用。为了提高估算的空间精度,研究者开始将Landsat(30 m)、Sentinel-2(10 m)系列卫星遥感数据应用于水稻土区和黑土区SOC估算[1, 7]。同时,偏最小二乘算法、弹性网络及随机森林[6–11]等机器学习方法的应用,为SOC估算提供了坚实的理论基础。
在宏观尺度上,SOC受气象、土壤、地形以及植被等自然因素的复杂影响,导致其在水平和垂直方向上呈现显著分异[6, 10]。然而,在小尺度区域,如以潮土为主的豫北平原耕作区,其地貌特征相对均一,气象和土壤的空间异质性较小,各环境因素对SOC的影响机制将发生变化,探究不同环境因子组合下SOC估算模型精度变化情况,以及各环境因子对模型的具体贡献度,均是当前亟需深入研究的问题。
河南是全国粮食大省,其SOC水平关系到农作物的产量和质量,对保障国家粮食安全具有显著影响。基于此,本文将有“豫北粮仓”之称的滑县作为研究区,基于实测耕作层SOC和Sentinel-2高分辨率卫星遥感反射率和光谱指数数据,辅以气象、土壤、地形及人类活动等因子,综合分析各因子中不同变量与SOC的相关性,定量评估不同机器学习方法在不同因子组合下的表现,旨在构建高精度的SOC估算模型,探究其最佳因子和关键变量,揭示SOC空间变异规律。
1 材料与方法 1.1 研究区概况研究区为河南省东北部的滑县(114°25′ E ~ 114° 57′ E,35°13′ N ~ 35°39′ N)(图 1),总面积1 814 km2,耕地面积1 340 km2。该县海拔高度29 ~ 71 m,地势西高东低,以平原为主,年均气温13.7℃,平均降水量634.3 mm,日照时数2 365.5 h,无霜期201 d,温带季风气候。耕地以潮土为主[12],春季主种小麦,秋季主种玉米。
|
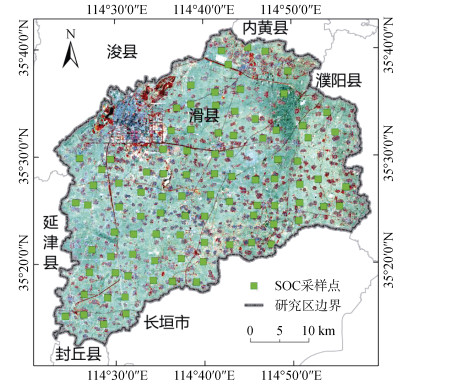
图 1 研究区地理位置及SOC样方点分布 Fig. 1 Locations of study area and SOC sampling sites |
2023年2月开展土样野外采集工作。在研究区内,构建3 km × 3 km网格,基于网格内耕地面积占比,结合代表性和均匀性原则,筛选出92个土样采集样方,在每个样方内,随机选择30 m × 30 m的样地(图 1),按照“S”形路线,每隔10 m取1钻土,共取10钻土混合成1个土样,取样深度20 cm。所有土样经自然风干、研磨、过筛处理,利用重铬酸钾氧化滴定法测定SOC含量。数据采集过程中,部分田块刚进行翻耕、浇水或施肥等农事活动,导致数据存在离群情况,因此,本文以四分位数和四分位距为基础的箱型图法剔除异常点,最后保留85个样本数据用于后续模型构建。
1.3 其他数据来源及预处理卫星遥感数据选择裸土期(2022年10月19日) Sentinel-2的L2A产品,来自哥白尼数据空间生态系统,该产品包含12个波段(B1 ~ B12),中心波长443 ~ 2 190 nm,均已经过大气校正和几何精校正。基于该数据提供的BOA_QUANTIFICATION_VALUE和BOA_ADD_OFFSET参数,利用ENVI 5.6进行增益值计算,获取地表反射率数据。同时,计算生成卫星遥感数据衍生的光谱指数数据,一是使用增强植被信号较好的归一化差值指数(NDVI)和土壤调节植被指数(SAVI)[13-14];二是使用增强裸土信息较好的裸土指数(BSI)、增强型裸土指数(EBSI)、归一化差值裸地与建筑用地指数(NDBBI)和归一化土壤指数(NDSI)[15-16, 9]。
气象数据包括2022年平均潜在蒸散发、气温和降水量,来自国家青藏高原科学数据中心,空间分辨率为1 km。土壤数据包括土壤容重、黏粒、砂粒和粉粒,来自时空三极环境大数据平台,空间分辨率为250 m。DEM数据来自NASA阿拉斯加卫星设备处的ALOS,空间分辨率为12.5 m,并通过SAGA 9.3计算坡度、坡向、地形位置指数(TPI)、汇流动力指数(SPI)和地形粗糙指数(TRI)等变量。人类活动数据是在道路、居民点等第三次全国国土调查数据基础上,生成代表人类活动强弱的最近欧式距离栅格数据,空间分辨率10 m。
为最大限度发挥Sentinel-2的高空间分辨率优势,提升SOC估算精度,采用ArcGIS 10.2软件的最邻近插值法,将气象、土壤和地形数据重采样至10 m×10 m栅格,空间参考系统也统一转换至UTM50,确保所有数据空间尺度及位置保持一致。
1.4 研究方法 1.4.1 偏最小二乘偏最小二乘(Partial least square,PLS)是Herman Word提出的统计学方法[17],其对自变量和因变量重新投影,在新坐标系中,将对原自变量贡献率最强的前几位新变量作为主成分,减少原自变量间多重共线性冗余信息,最后通过多元线性回归进行分析。PLS通过Python语言sklearn库的PLSRegression函数实现。
1.4.2 弹性网络弹性网络(Elastic net,EN)是Zou和Hastie [18]提出的算法,用于解决多重共线性问题。它通过一个混合惩罚项(α)来“弹性”结合Lasso和Ridge回归的优点,当α为0时,等价于Ridge回归;当α为1时,等价于Lasso回归;当α在(0, 1)时,EN兼具两者特性。EN通过Python语言sklearn库的ElasticNet函数实现。
1.4.3 随机森林随机森林(Random forest,RF)由Breiman[19]提出,通过bootstrap抽样法,多次随机有放回地将原始数据分为袋内和袋外随机样本,每次训练袋内样本子集,生成大量相互独立的决策树组成随机森林,并用相应袋外数据的误差评估最佳回归树数量和最优分裂节点数,所有决策树预测平均值作为回归的最终值。RF通过Python语言sklearn库的RandomForestRegressor函数实现。
1.5 评价指标采用决定系数(R2)、性能与四分位距之比(RPIQ)、平均绝对误差百分比(MAPE)对模型进行评估。R2越接近1,预测值与实际值拟合度越好,精度越高。MAPE是预测值与实际值的误差百分比,值越小,预测结果越准确。RPIQ兼顾预测值误差和实际值变化,值越大,模型性能越好[20]。
2 结果与分析 2.1 土壤有机碳描述性统计根据7∶3原则,研究区85个样本数据中59个用于训练集,26个用于验证集。总样本SOC含量介于5.86 ~ 11.56 g/kg,平均为7.98 g/kg,变异系数为11.70%,表明总样本呈现弱中等变异性(表 1)。训练集和验证集的统计特性与总样本相似。
|
|
表 1 SOC含量描述性统计 Table 1 Descriptive statistics of SOC content |
利用SPSS 27软件计算SOC含量与反射率光谱(R)、光谱指数(I)、气象(M)、土壤(S)、DEM(D)和人类活动(H)因子中不同变量的Pearson相关性(表 2),结果显示,SOC与各类因子中不同变量的相关性大小存在显著差异。SOC与R因子的相关性随波长变化呈现“W”形模式,其中与中心波长为2 190 nm(B12)和440 nm(B1) 的反射率光谱相关性极显著。SOC与I因子中的裸土指数呈负相关,与植被指数呈正相关,且与多数裸土指数的相关性强度大于其与植被指数的相关性,如SOC与NDSI、BSI和NDBBI的相关性大于SOC与NDVI和SAVI的相关性。SOC与M因子中的潜在蒸散发和气温呈极显著负相关,而与降水量呈显著正相关。SOC与S因子的容重和粉粒呈极显著相关,而与黏粒则相关性不显著。SOC与D因子均呈负相关,但仅与高程的相关性极显著。SOC与H因子呈正相关,且仅与居民点距离的相关性显著。
|
|
表 2 SOC与各类因子中变量的相关性 Table 2 Correlations between SOC contents and different variables in various factors |
鉴于变量间存在多重共线性问题,并非所有变量都会对SOC估算产生显著影响[21],本文采取分步筛选变量策略:首先,从每类因子中筛选出与SOC相关性最强的单一变量,即B12、NDSI、潜在蒸散发、容重、高程和居民点距离;其次,在R、I、M和S因子中,若有两个以上变量与SOC呈(极)显著相关,则在上步基础上再添加一个相关性最强的变量代表该因子,即B1、BSI、气温和粉粒。最终,有10个变量进入后续模型构建,在适当控制变量多重共线性问题的同时,又确保了模型估算能力。
2.3 土壤有机碳估算模型及精度检验 2.3.1 环境因子组合根据R、I、M、S、D和H因子与SOC相关性强度,依次添加不同因子,采用10折交叉验证的格网搜索方法构建EN、PLS和RF模型(表 3)。EN模型在R、I、M、S和D因子依次添加后,R2从0.27持续增至0.47,RPIQ也达到最高值2.29;随着H因子加入后,R2和RPIQ均出现降低,表明H因子降低了EN模型精度;然而,EN模型的MAPE却在R+I+M因子组合下达到最低值6.82。PLS模型在R、I、M、S和D因子依次添加后,R2从0.32持续增至0.54;尽管加入H因子后,R2略有下降,但RPIQ和MAPE却有所改善,表明H因子在一定程度上可提高PLS模型精度;然而,PLS模型的RPIQ和MAPE却在R和I因子组合下达到最佳值1.46和10.37。RF模型在R、I、M和S因子依次添加后,R2从0.39持续增至0.63,RPIQ和MAPE也分别达到最佳的2.75和5.86,表明此因子组合下RF模型精度最佳;然而,当加入D和H因子后,3个指标均显示RF模型性能下降。
|
|
表 3 不同因子组合下模型精度对比 Table 3 Accuracy comparisons of various models under various factor combinations |
3个评价指标中,有2个以上显示为最优,则可判定该因子组合为最佳因子组合。综上,EN、PLS和RF模型最佳因子组合分别为R+I+M+S+D、R+I和R+I+M+S。
2.3.2 精度对比RF模型的最大R2为0.63,较EN和PLS模型分别提高34.04% 和15.81%,说明RF模型能更好拟合SOC变化;RPIQ方面,RF模型得分最高(2.75),优于EN模型(2.29)和PLS模型(1.46),依照RPIQ评估标准[20]可知,RF模型估算最为精准。此外,RF模型的MAPE最低(5.86),其估算准确率达94.14%,较EN和PLS模型分别增加1.03和4.51个百分点。
综上,3个评价指标均显示RF模型优于EN和PLS模型,其中2个评价指标显示EN模型优于PLS模型。因此,模型整体精度为:RF > EN > PLS。
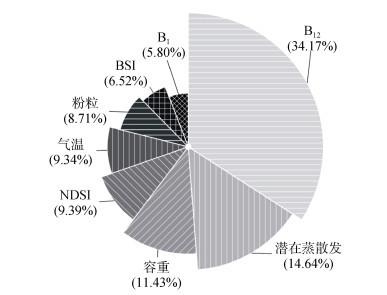
2.3.3 变量重要性计算RF模型各变量的重要性(图 2),结果显示,R因子对SOC估算贡献最大(39.97%),其次为M因子(23.98%)、S因子(20.14%)和I因子(15.91%)。其中,R因子中B12(34.17%) > B1 (5.8%),M因子中潜在蒸散发(14.64%) > 气温(9.34%),S因子中容重(11.43%) > 粉粒(8.71%),I因子中NDSI (9.39%) > BSI(6.52%),表明虽然上述变量均与SOC显著相关,但它们对估算SOC的贡献程度不同。重要性排名前4位的变量依次为B12、潜在蒸散发、容重和NDSI,累积贡献率达69.63%,它们作为4类因子的代表,是SOC估算的关键变量。
|
图 2 RF模型的变量重要性 Fig. 2 Importance of variables in RF model |
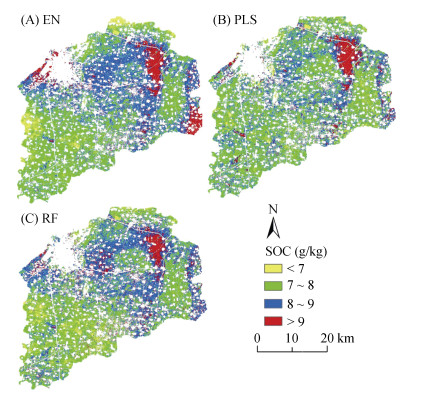
以耕地矢量数据为边界,分别绘制EN、PLS和RF模型在其最佳因子组合下的SOC空间分布预测图(图 3)。结果显示,3个模型估算的SOC空间分布整体相似,呈东北高、西南低趋势。SOC值域范围差距明显(表 4),EN模型(3.32 ~ 13.73 g/kg)和PLS模型(5.14 ~ 14.97 g/kg)的估算结果相较于总样本(5.86 ~ 11.56 g/kg),波动性大,稳定性差,而RF模型估算结果(6.15 ~ 11.08 g/kg)更接近于总样本,说明RF模型既能很好描述研究区SOC空间差异,又能确保结果稳定。RF模型估算的SOC均值为8.16 g/kg,低于全国平均值(22.28 g/kg)[6]。其中,中值区占比最高,占耕地总面积78.82% 以上,主要分布在研究区中部;低值区和高值区占比为6.37% 和14.81%,分别分布在研究区西南部和东北部。
|
图 3 不同模型估算的SOC空间分布 Fig. 3 Spatial distribution of SOC contents estimated by different models |
|
|
表 4 不同模型估算的SOC基本统计特征 Table 4 Basic statistical characteristics of SOC contents estimated by different models |
SOC分布受多重因素影响,往往表现为复杂的非线性关系[22]。相较于EN和PLS模型,RF模型通过构建不同决策树,并考虑变量间多种分割和相互作用,更能精确模拟非线性关系[23]。本研究表明,在样本点拟合、估算结果分布范围等方面,RF模型优于EN和PLS模型,与先前研究[24, 11]结论一致。
此外,RF模型估算结果受SOC与各类因子相关性强弱的影响[10]。如,当加入与SOC相关性强的R和M因子时,模型精度显著提升,但加入与SOC相关性较弱的高程及居民点距离时,模型精度不升反降。因此,构建RF模型时,应慎重选择与SOC相关性强的变量,以此提高其估算能力。
3.2 最佳因子及关键变量在R、I、M和S因子组合下,RF模型精度最高,使该因子组合成为研究区SOC估算的最佳因子。模型重要性揭示,B12、潜在蒸散发、土壤容重和NDSI对RF模型的累积贡献度达69.63%,是模型的关键变量。原因可能是:①B12中心波长2 190 nm,该波段能敏感地捕捉裸土信息,表现与SOC空间变异直接对应的光谱值,与Suleymanov等[23]结论一致;②潜在蒸散发反映干旱程度和水资源状况,值升高说明干旱趋势加剧,孔隙度变大,颗粒更加松散,风蚀风险变大,SOC积累少、流失多,与Li等[25]结论一致;③土壤容重反映土壤的通气透水性和孔隙度[22],该值增加说明土壤通气性变差,微生物因氧气供给受限而活动性减弱,从而降低了SOC含量,与Wang等[26]结论一致;④NDSI能增强裸土反射特性,值越大,土壤暴露程度越严重,水分越少,植被生长和土壤微生物活性减弱,SOC含量下降,与闫蒙等[27]结论一致。
同时,气温、粉粒、BSI和B1变量对RF模型也有一定的贡献度,累积达30.37%,部分原因是:①气温升高会促使K-策略为主的微生物群落提高分解活动和土壤呼吸,以维持其代谢所需能量,降低有机合成碳分配,促使SOC含量下降[28];②粉粒因颗粒细,表面积大,利于提高土壤的保水性和通气性,有更多正电荷与土壤中带负电荷的腐殖质结合[27],促进有机质吸附,增加SOC积累,这与多个研究结论一致[22, 27]。
另外,地形不能成为本研究区SOC估算模型的重要因子,因高程的加入仅略微提高了EN模型的R2和RPIQ,及PLS模型的R2,而RF模型精度却未得到提升。该结论与部分研究结果不一致[6, 10-11],可能是因为研究区地形起伏不大(29 ~ 71m),该因子无法精准描述SOC的空间异质性。同时,居民点距离也不能提高RF模型和EN模型精度,仅对PLS模型的RPIQ和MAPE指标有相应的微弱提升,可能与人类活动对土壤的随机性干扰有关。
3.3 误差分析SOC估算模型的R2大多小于0.4[7]。本研究区为小尺度的平原区,各类因子空间异质性较低,模型R2达0.63,高于现有部分研究结果[7, 21],处于中上等水平,但仍低于个别研究[8, 29],可能误差源为:①本文对气象、土壤及地形因子数据进行了空间尺度的向上重采样,该操作会因尺度变换而引入误差;②SOC与各类因子关系复杂,本文参与模型构建的仅是各因子中与SOC呈(极)显著相关的变量,并不能全部解释SOC的空间变异。
本文提出了一种利用Sentinel-2卫星影像、气象和土壤因子快速估算SOC的技术方法,揭示了平原区耕作层SOC估算中的最佳因子及关键变量,不仅为提高SOC估算精度提供了理论依据,而且为因地制宜增强农业综合生产力提供了方法支撑。未来应进一步探究不同尺度因子及多时相卫星遥感数据对SOC估算精度的影响。
4 结论以河南省滑县为研究区,基于SOC样本数据,融合R、I、M、S、D及H类因子数据,探究估算SOC的最佳模型、最佳因子、关键变量,结果显示:①各类因子中均有变量与SOC呈(极)显著相关;②不同因子组合下,RF模型在精度和空间异质性描述方面均优于EN和PLS模型;③RF模型在R、I、M和S最佳因子的组合下,表现出了最高估算精度,R2为0.63,RPIQ为2.75,MAPE为5.86,其中,B12、潜在蒸散发、容重和NDSI的累积贡献率达69.63%,成为SOC估算的关键变量;④RF模型估算结果显示,研究区SOC含量呈东北高、西南低的空间分布趋势,变动范围为6.15 ~ 11.08 g/kg,表现出弱中等变异性,平均值为8.16 g/kg,含量相对较低,低于全国平均值(22.28 g/kg)。
| [1] |
杨佳佳, 林楠, 于秀秀, 等. 东北典型黑土区有机碳遥感定量反演研究[J]. 地质与资源, 2020, 29(4): 357-362 (  0) 0) |
| [2] |
Summers D, Lewis M, Ostendorf B, et al. Visible near- infrared reflectance spectroscopy as a predictive indicator of soil properties[J]. Ecological Indicators, 2011, 11(1): 123-131 DOI:10.1016/j.ecolind.2009.05.001 (  0) 0) |
| [3] |
罗德芳, 彭杰, 冯春晖, 等. 可见光-近红外、中红外光谱的土壤有机质组分反演[J]. 光谱学与光谱分析, 2021, 41(10): 3069-3076 (  0) 0) |
| [4] |
赵昕, 张晓光, 宋祥云, 等. 胶莱平原县域表土有机碳空间变异特征研究及自相关分析[J]. 干旱区资源与环境, 2023, 37(4): 127-136 (  0) 0) |
| [5] |
朱阳春, 张振华, 赵学勇, 等. 河套灌区土壤有机碳和总碳的空间异质性及相关性分析[J]. 江苏农业学报, 2017, 33(6): 1294-1300 DOI:10.3969/j.issn.1000-4440.2017.06.014 (  0) 0) |
| [6] |
罗梅, 郭龙, 张海涛, 等. 基于环境变量的中国土壤有机碳空间分布特征[J]. 土壤学报, 2020, 57(1): 48-59 (  0) 0) |
| [7] |
吴启航, 姚园, 李一凡, 等. 福建省漳州市水稻物候特征对稻田土壤有机碳制图的影响[J]. 土壤学报, 2024, 61(2): 385-397 (  0) 0) |
| [8] |
赵启东, 葛翔宇, 丁建丽, 等. 结合分数阶微分技术与机器学习算法的土壤有机碳含量光谱估测[J]. 激光与光电子学进展, 2020, 57(15): 253-261 (  0) 0) |
| [9] |
牛芳鹏, 李新国, 麦麦提吐尔逊·艾则孜, 等. 基于光谱指数的博斯腾湖西岸湖滨绿洲土壤有机碳含量估算模型[J]. 江苏农业学报, 2022, 38(2): 414-421 DOI:10.3969/j.issn.1000-4440.2022.02.015 (  0) 0) |
| [10] |
袁玉琦, 陈瀚阅, 张黎明, 等. 基于多变量与RF算法的耕地土壤有机碳空间预测研究——以福建亚热带复杂地貌区为例[J]. 土壤学报, 2021, 58(4): 887-899 (  0) 0) |
| [11] |
卢宏亮, 赵明松, 刘斌寅, 等. 基于随机森林模型的安徽省土壤属性空间分布预测[J]. 土壤, 2019, 51(3): 602-608 (  0) 0) |
| [12] |
李笑莹, 张学雷, 任圆圆. 河南省土壤及地形与耕地多样性格局的特征[J]. 土壤, 2019, 51(4): 775-785 (  0) 0) |
| [13] |
贾德伟, 周磊, 黄灿辉, 等. 基于MODIS数据的冬小麦雹灾空间分布信息提取研究——以河南省平顶山市为例[J]. 地域研究与开发, 2018, 37(6): 134-138 (  0) 0) |
| [14] |
彭燕, 何国金, 张兆明, 等. 中国区域Landsat遥感指数产品[J]. 中国科学数据, 2020, 5(4): 83-90 (  0) 0) |
| [15] |
李虎, 钟韵, 冯雅婷, 等. 无人机遥感的多植被指数土壤水分反演模型[J]. 光谱学与光谱分析, 2024, 44(1): 207-214 (  0) 0) |
| [16] |
吴志杰, 赵书河. 基于TM图像的"增强的指数型建筑用地指数" 研究[J]. 国土资源遥感, 2012, 24(2): 50-55 (  0) 0) |
| [17] |
刘潜, 王梦迪, 郭龙, 等. 基于机载高光谱影像的农田尺度土壤有机碳密度制图[J]. 遥感学报, 2024, 28(1): 293-305 (  0) 0) |
| [18] |
Zou H, Hastie T. Regularization and variable selection via the elastic net[J]. Journal of the Royal Statistical Society Series B: Statistical Methodology, 2005, 67(2): 301-320 (  0) 0) |
| [19] |
Breiman L. Random forests[J]. Machine Learning, 2001, 45: 5-32 (  0) 0) |
| [20] |
王瑾杰, 丁建丽, 葛翔宇, 等. 分数阶微分技术在机载高光谱数据估算土壤含水量中的应用[J]. 光谱学与光谱分析, 2022, 42(11): 3559-3567 (  0) 0) |
| [21] |
周琪清, 赵小敏, 郭熙, 等. 基于物候与极端气候信息的耕地土壤有机碳空间分布预测研究[J]. 土壤学报, 2024, 61(3): 648-661 (  0) 0) |
| [22] |
常琳溪, 梁新然, 王磊, 等. 中国稻田土壤有机碳汇特征与影响因素的研究进展[J]. 土壤, 2023, 55(3): 487-493 (  0) 0) |
| [23] |
Suleymanov A, Abakumov E, Nizamutdinov T, et al. Soil organic carbon stock retrieval from Sentinel-2A using a hybrid approach[J]. Environmental Monitoring and Assessment, 2023, 196(1): 23 (  0) 0) |
| [24] |
杨珺婷, 李晓松. 应用哨兵2号卫星遥感影像数据和机器学习算法对锡林郭勒草原土壤表层有机碳及全氮的估算[J]. 东北林业大学学报, 2022, 50(1): 64-71 (  0) 0) |
| [25] |
Li C J, Fu B J, Wang S, et al. Drivers and impacts of changes in China's drylands[J]. Nature Reviews Earth & Environment, 2021, 2: 858-873 (  0) 0) |
| [26] |
Wang Y Q, Shao M A, Liu Z P, et al. Prediction of bulk density of soils in the Loess Plateau Region of China[J]. Surveys in Geophysics, 2014, 35(2): 395-413 (  0) 0) |
| [27] |
闫蒙, 王旭洋, 周立业, 等. 科尔沁沙地沙漠化过程中土壤有机碳含量变化特征及影响因素[J]. 中国沙漠, 2022, 42(5): 221-231 (  0) 0) |
| [28] |
Li H, Yang S, Semenov M V, et al. Temperature sensitivity of SOM decomposition is linked with a K-selected microbial community[J]. Global Change Biology, 2021, 27(12): 2763-2779 (  0) 0) |
| [29] |
李宏达, 李德成, 曾荣. 基于光谱相似性匹配的土壤有机碳估算[J]. 土壤学报, 2021, 58(5): 1224-1233 (  0) 0) |
 2024, Vol. 56
2024, Vol. 56


