2. 江西省环境岩土与工程灾害控制重点实验室, 江西赣州 341000
模拟非饱和土壤水分运动,可通过求解符合边界条件的Richards方程实现[1-4],该方法对涉及水分入渗的实际工程具有重要意义。而测定土壤水力特性是求解Richards方程的关键之一[5-8],其中土壤水分扩散率是模拟土壤水分水平入渗运动的重要参数,并且可作为测试土水特征曲线的中间参数,用于简化土水特征曲线测试[9]。因此,建立准确测定土壤水分扩散率的方法具有重要意义。
测试土壤水分扩散率的方法主要分为基于水流入渗过程的反演方法和基于水平入渗试验的直接测试法。Gardner[10]提出利用压力盘出流数据来反演土壤水力特性,其中包括反演土壤水分扩散率。反演方法通过水流入渗试验中的特定数据结合水流入渗模型能有效估计相应的土壤水力特性参数[11-14]。但是反演方法受解的非唯一性影响,需要严格的边界条件和特定的水流入渗过程数据才能减小其影响[15-18]。Bruce和Klute[19]提出利用一维水平试验测试土壤水分扩散率的水平入渗法,该方法操作简单,但是在收集试验数据时容易出现较大的误差[20-23]。Evangelides等[24]通过记录湿润锋随时间运动情况,结合累计入渗量,利用其构造的函数计算土柱剖面含水率分布,最终计算出土壤水分扩散率,该方法避免了测试土壤含水率的误差,但并没有较可靠的记录湿润锋位置变化的方法,可能会影响结果的准确性。Villarreal等[25]在试验土柱上布置水分传感器记录特定位置处含水率随时间变化数据,以替代土柱剖面含水率分布数据,但由于存在边界效应,该方法的传感器摆放位置会对结果造成一定影响。为减小边界效应影响,帅嘉伟等[26]提出求解一维水平入渗Richards方程在第一类边界条件下的近似解析解,基于近似解析解,修正受边界影响的数据,再采用水平入渗法确定土壤水分扩散率,虽然该方法能降低边界效应影响,但是受含水率测试误差的影响较大。
为了降低测试误差对水平入渗法测试结果的影响,本文结合Van Genuchten(VG)模型[27]和Philip法[28],先预设模型参数,采用Philip法计算不同体积含水率对应的Boltzmann参数[19],量化计算值与测试值的误差,再通过优化算法确定模型参数,以此建立具有抵抗测试误差能力的迭代法确定土壤水分扩散率,并通过数值模拟和文献数据验证该方法的合理性,以期为涉及水分入渗的实际模拟提供准确参数。
1 研究方法与数据来源 1.1 一维水平入渗基本方程一维水平入渗可以采用一维水平Richards方程描述,如式(1)所示;对于第一类边界条件下,无限长水平入渗的定解条件如式(2)所示[29-30]。
| $ \frac{{\partial \theta }}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {D\frac{{\partial \theta }}{{\partial x}}} \right) $ | (1) |
| $ \left\{ \begin{array}{l} \theta \left( {x = 0, t \geqslant 0} \right) = {\theta _{\text{0}}} \hfill \\ \theta \left( {x > 0, t = 0} \right) = {\theta _{{\text{ini}}}} \hfill \\ \theta \left( {x \to \infty , t \geqslant 0} \right) = {\theta _{{\text{ini}}}} \hfill \end{array} \right. $ | (2) |
式中:t为时间,d;x表示水平坐标,本文以土柱最左端为原点、水平向右为正方向,m;θ为体积含水率,m3/m3;D为土壤水分扩散率,是体积含水率的函数,D=D(θ),m2/d;θ0和θini分别为进水端边界土壤含水率和初始含水率,m3/m3。
第一类边界条件下,采用Boltzmann变换处理式(1),可以得到式(3)[31]:
| $ \int_{{\theta _{{\text{ini}}}}}^\theta {\lambda {\text{d}}\theta } = - 2D(\theta )\frac{{{\text{d}}\theta }}{{{\text{d}}\lambda }} $ | (3) |
式中:λ为Boltzmann变换参数,λ = x/t0.5,m/d0.5。
1.2 Philip法式(3)给出了λ随θ变化的隐式关系,当给定土壤水分扩散率D时,为了计算不同θ对应的λ,Philip提出了一种求解方法,具体计算步骤如下[31]:
1) 将含水率区间[θ0, θini]等分为n份,分别记为θ0、θ1、θ2、…、θi、…、θn,其中θ0 = θ0,θn = θini,步长Δθ = (θ0−θini)/n,将各个体积含水率代入D – θ的关系式中,即可得到Di(i = 0, 1, 2, …, n),将Di代入式(4)中,得到土壤水分扩散率的加权平均值
| $ \bar D = \frac{2}{{{n^2}}}\sum\limits_{i = 0}^n {\left( {n - i} \right){D_i}} $ | (4) |
| $ {D_{i + {1 / 2}}} = \frac{{{D_i} + {D_{i + 1}}}}{2} $ | (5) |
式中:n和i分别为含水率区间等分份数及编号;
2) 采用式(6)计算λ1,然后交替采用式(7)和式(8)计算Ii+1/2和λi(i = 1, 2, …, n−1)。
| $ {\lambda _1} = {{2{D_{{1 / 2}}}} / {{I_{{1 / 2}}}}} $ | (6) |
| $ {I_{i + {1 / 2}}} = {I_{\left( {i - 1} \right) + {1 / 2}}} - {\lambda _i} $ | (7) |
| $ {\lambda _{i + 1}} = {\lambda _i} + {{2{D_{{{i + 1} / 2}}}} / {{I_{{{i + 1} / 2}}}}} $ | (8) |
式中:Ii+1/2为简化计算引入的迭代变量。
3) 采用式(9)计算Ii+1/2的迭代初始值I1/2。
| $ {I_{{1 / 2}}} = 2n\sqrt {{{\bar D} / {\rm{ \mathsf{ π}}}}} $ | (9) |
4) 采用式(10)计算参数y,采用式(11)计算参数A;再分别采用式(12)和式(13)计算
| $ y = \frac{{{\lambda _{n - 1}}}}{{2\sqrt {{D_{n - {1 / 2}}}} }} $ | (10) |
| $ A = \frac{{2y{{\text{e}}^{ - {y^2}}}}}{{\sqrt {\rm{ \mathsf{ π}}} {\text{erfc}}\left( y \right)}} - 2{y^2} $ | (11) |
| $ I_{n - {1 / 2}}^{\text{F}} = {I_{\left( {n - 2} \right) + {1 / 2}}} - {\lambda _{n - 1}} $ | (12) |
| $ I_{n - {1 / 2}}^{\text{S}} = \frac{{{\lambda _{n - 1}}}}{2} + \frac{{2{D_{n - {1 / 2}}}A}}{{{\lambda _{n - 1}}}} $ | (13) |
| $ \Delta = \left| {I_{n - {1 / 2}}^{\text{F}} - I_{n - {1 / 2}}^{\text{S}}} \right| $ | (14) |
式中:Δ为迭代误差;
5) 给定最大允许误差值[Δ],若Δ≤[Δ],θi对应的λi即为所求结果;若Δ > [Δ],采用式(15)修正I1/2的值,重复上述步骤3)、4)和5),直至Δ≤[Δ]。
| $ {I_{{1 / 2}}} = {I_{{1 / 2}}} - \frac{{\mathit{\Delta }}}{2} $ | (15) |
1) 试验数据为θ – x数据。某一时刻,得到了水平入渗土柱上不同位置的体积含水率(即θ – x数据),采用λ = x/t0.5,将θ – x数据转化为θ – λ数据,λtest, 0、λtest, 1、…、λtest, k、…、λtest, N对应的体积含水率分别为θtest, 0、θtest, 1、…、θtest, k、…、θtest, N,测试土柱的初始含水率θini、稳定含水率θ0和饱和含水率θs。采用VG模型量化土壤水分扩散率随体积含水率的变化规律(式(17)),给定参数[θr, m, Ds],设定n和[Δ]的值,采用1.2节介绍的Philip法,即可得到θ1、θ2、…、θi、…、θn对应λ的计算值,分别记为λcal, 1、λcal, 2、…、λcal, i、…、λcal, n。同时,当θ = θ0时,对应λ的值为0,则λcal, 0 = 0;当θ = θini时,对应λ的值为∞,为了避免Philip法的计算结果出现∞,采用试验数据中λ的最大值λmax代替λcal, n。采用插值算法处理θ – λ数据的计算值,得到λtest, 0、λtest, 1、…、λtest, k、…、λtest, N对应体积含水率的计算值θcal, 1、θcal, 2、…、θcal, k、…、θcal, N。以体积含水率的试验值和计算值的平方和作为计算误差(式(18)),采用内点法搜索计算误差最小时对应的参数[θr, m, Ds],将得到的参数代入式(17),即可得到土壤水分扩散率D(θ)。由于采用的Philip法是通过迭代的方式计算λ,因而本文将提出的方法称为迭代法。
| $ D = \frac{{{D_{\text{s}}}{{\left[ {1 - {{\left( {1 - {{\mathit{\Theta}} ^{1/m}}} \right)}^m}} \right]}^2}}}{{{{\mathit{\Theta}} ^{\left( {m + 2} \right)/\left( {2m} \right)}}{{\left( {{{\mathit{\Theta}} ^{ - 1/m}} - 1} \right)}^m}}} $ | (17) |
| $ \xi = \sum\limits_{k = 1}^N {{{\left( {{\theta _{{\text{test}}, k}} - {\theta _{{\text{cal}}, k}}} \right)}^2}} $ | (18) |
式中:Θ为标准化含水率,Θ = (θ–θr)/(θs–θr),θr和θs分别为残余和饱和含水率,m3/ m3;Ds = Ks/[nmα (θs–θr)],m2/d,其中n、m和α为土柱孔隙分布相关的参数,m = 1–1/n,Ks为饱和渗透系数,m/d;θtest和θcal分别体积含水率的试验值和计算值,m3/ m3;ξ为体积含水率计算误差。
2) 试验数据为θ – t数据。在土柱上布置监测点,监测该位置体积含水率随时间的变化(即θ – t数据),采用λ = x/t0.5,将θ – t数据转化为θ – λ数据,采用文献[26]的方法确定受边界效应影响的临界含水率θlim,以[θini, θlim]范围内的θ – λ数据作为基础数据。之后,计算土壤水分扩散率的过程与试验数据为θ – x数据时相同,不再赘述。
1.4 数据来源通过数值模拟数据及他人一维水平入渗试验数据验证本文方法,其中,数值模拟数据通过Hydrus-1D软件获取,他人试验数据引用Villarreal等[25]、帅嘉伟等[26]和雷志栋[31]研究中的一维水平入渗试验数据。利用数值模拟及他人试验中的θ – x数据和θ – t数据确定一维水平入渗率,再与对应一维水平入渗率的真实值比较,验证方法的可靠性。
1.5 Hydrus-1D数值模拟试验采用Hydrus-1D软件模拟水分在壤砂土、砂壤土、砂质黏壤土和壤土4种土柱中的一维水平入渗过程。土柱的长度设置为1 m,土壤水分扩散率与体积含水率的关系采用VG模型描述,4种土柱的VG模型参数如表 1所示[27]。左边界(x = 0)设置为定含水率边界(θ = θ0),右边界(x = L,L为土柱长度,m)设置为自由排水边界,初始时刻土柱的含水率为θini,4个土柱θ0和θini的取值也列于表 1。在x = 0.25 m处布置测点,监测测点处体积含水率θ随时间t的变化(θ – t数据)。
|
|
表 1 基本参数[27] Table 1 Basic parameters |
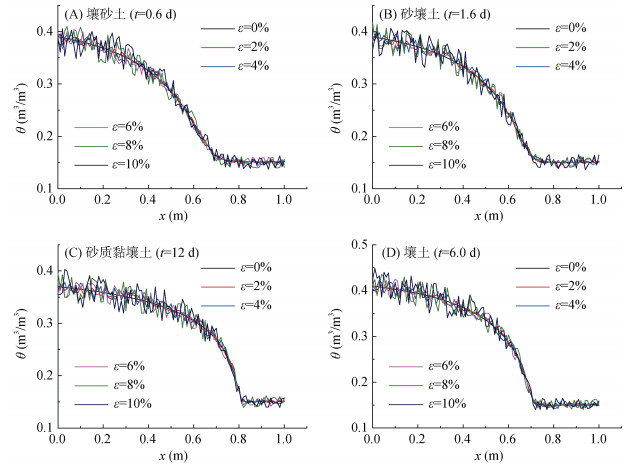
4种土体分别在t=0.6、1.6、12和6.0 d时,体积含水率随坐标变化的Hydrus-1D模拟结果如图 1所示。模拟结果通过式(19)引入随机误差,随机误差分别为0%、2%、4%、6%、8% 和10% 的结果也绘制于图 1。
| $ {\theta _\varepsilon } = \left[ {1 - 2\left( {{\text{rand}} - 0.5} \right)\varepsilon } \right]\theta $ | (19) |
|
图 1 体积含水率随坐标x的变化情况 Fig. 1 Change of volumetric water content with x coordinates |
式中:rand为取[0, 1]范围内的随机数运算;ε为随机误差;θε为带有随机误差的体积含水率,m3/m3。
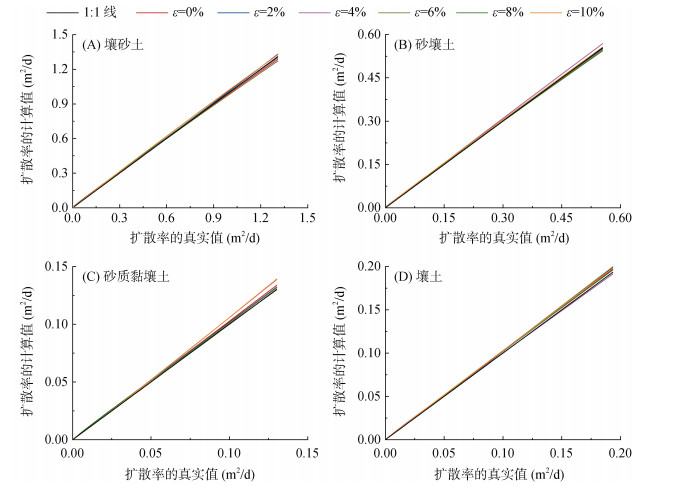
采用上述建立的迭代法分析图 1所示的数据,得到[θr, m, Ds]结果如表 2所示,将参数[θr, m, Ds]代入式(17)中,即可得到土壤水分扩散率的计算值,以理论值为横坐标,以计算值为纵坐标,展示土壤水分扩散率计算值与理论值的差异,结果如图 2所示。由图 2可知,不同测试误差的计算结果均分布在1︰1线附近,采用决定系数(式(20))量化计算值与理论值的误差,决定系数的结果也列于表 2。计算结果表明,当测试误差在[0, 10%]范围内时,决定系数均大于0.990 0,由此可见,迭代法的计算结果受体积含水率测试误差的影响较小。
| $ {R^2} = 1 - \frac{{\sum\limits_{i = 1}^N {{{\left( {{D_{{\text{theory, }}i}} - {D_{{\text{cal, }}i}}} \right)}^2}} }}{{\sum\limits_{i = 1}^N {{{\left( {{D_{{\text{theory, }}i}} - \frac{1}{N}\sum\limits_{i = 1}^N {{D_{{\text{theory, }}i}}} } \right)}^2}} }} $ | (20) |
|
|
表 2 迭代法分析θ–x数据的计算结果 Table 2 Calculation results of θ–x data analysis by iterative method |
|
图 2 采用迭代法分析Hydrus-1D数据得到的土壤水分扩散率计算值与理论值的比较 Fig. 2 Comparison of calculated value and theoretical value of soil water diffusivity obtained from Hydrus-1D data by iterative method |
式中:R2为决定系数;Dtheory为土壤水分扩散率的理论值;Dcal为土壤水分扩散率的计算值;i为体积含水率的编号;N为总体积含水率数据个数。
由表 2可知,对于壤土,不同的随机误差情况下,θr、m和Ds的计算结果分别在[0.000, 0.062]、[0.253, 0.448]和[0.188, 0.838]范围内变化,θr、m和Ds的变异系数CV(标准差与均值之比)分别为70.1%、19.8%和45.3%,由此可见,m值计算结果的波动最小,θr计算结果的波动最大。对于m值,CV∈[16%, 35%],说明m的计算结果具有中等变异性,对于θr和Ds,CV > 35%,说明θr和Ds的计算结果具有高度变异性。虽然3个参数计算结果的变异较大,但是土水特征曲线计算结果的决定系数大于0.990 0,说明总体计算误差较小,以下通过响应曲面法分析原因。
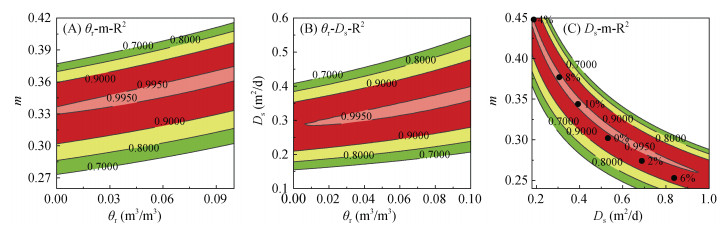
Hydrus-1D中,壤土VG模型参数[θr, m, Ds]的理论值为[0.078, 0.359, 0.352][27],将[θr, m, Ds]的理论值代入式(17)中,即可得到土壤水分扩散率的理论值Dtheory。同时改变两个参数的值,另一个参数取理论值,通过式(17)得到这种参数组合下土壤水分扩散率D,采用决定系数量化D与Dtheory的差异,则可以得到θr–m–R2、θr–Ds–R2和Ds–m–R2的响应曲面,结果如图 3所示。由图 3A和图 3B可知,响应曲面的等值线几乎相互平行,表明决定系数的变化对于θr不敏感,因而θr计算结果的变异系数较大,但是m和Ds取合适值时,不同的θr均能达到较大的决定系数。由图 3C可知,当给定θr时,决定系数为0.995 0对应的[m, Ds]参数组合呈月牙状,即在该范围的[m, Ds]参数值均能得到较为准确的土壤水分扩散率,说明参数[m, Ds]取值在有较大差异时,仍可得到与真实值相比差异较小的土壤水分扩散率。
|
图 3 壤土的VG模型参数对土壤水分扩散率影响的响应曲面 Fig. 3 Response surfaces of VG model parameters on soil water diffusivity in loam soil |
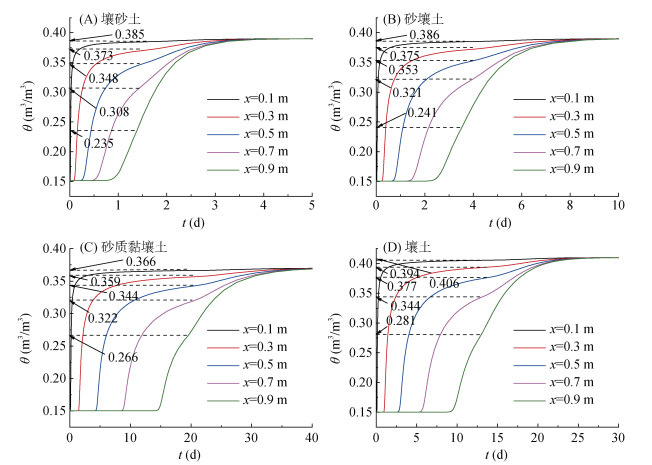
x=0.1、0.3、0.5、0.7和0.9 m处的体积含水率随时间的变化情况如图 4所示,采用文献[26]的方法确定受边界效应影响的临界含水率θlim,结果也列于图 4。随着监测点越靠近出水口,临界含水率越小,受边界效应影响的体积含水率范围越大。采用上述迭代法分析[θini, θlim]范围的θ – t数据,得到[θr, m, Ds]的计算值如表 3所示。仍然以壤土为例进行分析,θr、m和Ds的变异系数CV分别为96.7%、15.9%和40.2%,即当选择不同位置的θ – t数据分析时,θr和Ds具有较大的变异性。随着测点与入水口的距离增加,决定系数没有明显变化,决定系数均大于0.980 0。对于所分析的4种土体类型,当x=0.9 m时,不受边界效应影响的含水率区间分别为[0.150, 0.235]、[0.150, 0.241]、[0.150, 0.266]和[0.150, 0.281],得到的土壤水分扩散率的决定系数分别为0.998 5、0.998 7、0.997 9和0.998 4,均大于0.990 0。由此可见,受边界效应影响的临界含水率对计算结果的影响较小。
|
图 4 体积含水率随时间的变化情况 Fig. 4 Change of volumetric water content with time |
|
|
表 3 迭代法分析θ–t数据的计算结果 Table 3 Calculation results of θ–t data analysis by iterative method |
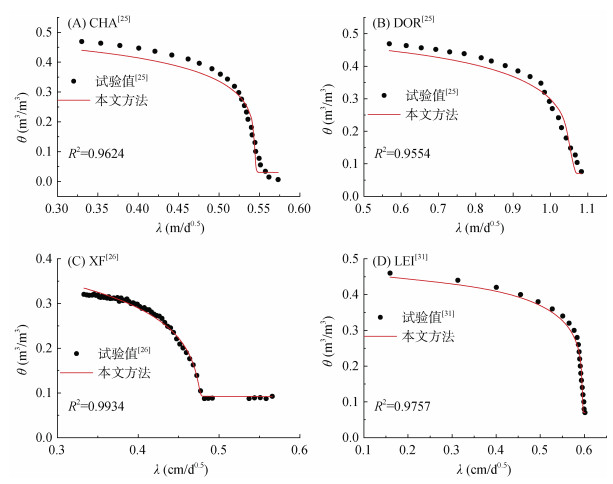
为了进一步通过试验数据验证本文提出方法的合理性,利用他人研究中的一维水平入渗试验数据进行验证(图 5,4种土柱分别为CHA[25]、DOR[25]、XF[26]和LEI[31])。采用迭代法分析时所需要的参数列于表 4,[θr, m, Ds]的计算结果也列于表 4。对于LEI[31],[θr, m, Ds]迭代法的计算结果为[0.034, 0.222, 8.131],将参数代入式(17),得到土壤水分扩散率如图 6所示,与水平吸渗法的结果进行对比,决定系数达到了0.891 5,将迭代法得到的土壤水分扩散率作为已知数据,采用Philip法计算λ随θ变化,结果如图 5D所示,与试验数据的决定系数为0.975 7。对于CHA[25]和DOR[25],土壤水分扩散率的计算结果分别如图 5A和图 5B所示,与试验数据进行比较,本文方法的决定系数分别为0.850 0和0.962 0,文献中经验模型的决定系数分别为0.500 3和0.713 3[25],本文方法优于经验模型,且对于体积含水率大于0.350 m3/m3对应土壤水分扩散率的结果,经验模型的决定系数分别仅为0.148 8和0.405 9,而本文方法分别为0.746 7和0.930 4,由此可见,本文方法可以弥补经验模型难以准确确定高体积含水率区间的土壤水分扩散率的不足。对于XF[26],测试数据为x = 0.45 m处的θ – t数据,临界含水率为0.321 m3/m3,[θr, m, Ds]迭代法的计算结果为[0.000, 0.218, 10.650],将参数代入式(17),得到土壤水分扩散率如图 6C所示,采用式(1)模拟一维水平入渗,得到x = 0.45 m处θ – t数据的计算值,并转化为θ–λ数据,结果如图 5C所示,其与试验值的决定系数为0.993 4。
|
图 5 文献中一维水平入渗数据及其迭代法模拟 Fig. 5 One-dimensional horizontal infiltration data and its iterative simulation in literatures |
|
|
表 4 文献中土柱的基本参数及迭代法计算结果 Table 4 Basic parameters of soil column in literature and calculation results of iterative method |
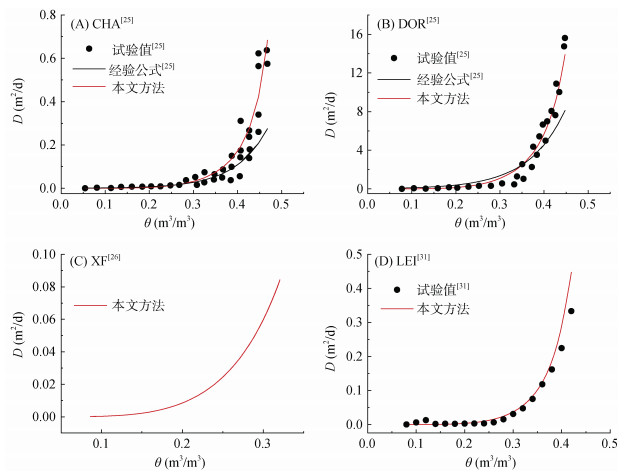
|
图 6 土壤水分扩散率迭代法的计算值与试验值的对比 Fig. 6 Comparison of calculated and experimental values of soil water diffusivity using the iterative method |
综上所述,采用迭代法分析试验数据,土壤水分扩散率的决定系数均在0.850 0以上,具有较高的精度,与Villarreal等[25]和帅嘉伟等[26]提出的方法相比,迭代法可以提高高含水率区域土壤水分扩散率计算结果的精度,同时受测试误差影响较小,迭代法具有较高的合理性。
3 结论本文结合VG模型和Philip法,先预设模型参数,采用Philip法得到θ – λ数据的计算值,再以决定系数量化计算值与测试值的误差,通过内点法优化模型参数,以此建立具有抵抗测试误差能力的迭代法,并通过数值模拟和文献数据验证了该方法的合理性,得到以下结论:
1) 采用迭代法分析测试误差0% ~ 10% 的θ – x数据,θr和Ds的变异系数大于35%,m的变异系数∈[16%, 35%],说明θr和Ds具有高度变异性,m具有中等变异性,将[θr, m, Ds]的结果代入VG模型,得到土壤水分扩散率计算结果的决定系数均大于0.995 0。由此可见,土壤水分扩散率的计算结果精度较高,且受测试误差的影响较小。
2) 对于θ – t数据,随着与入水口的距离增加,临界含水率θlim减小,不受边界效应影响的含水率范围[θini, θlim]越窄。采用迭代法分析不同位置处[θini, θlim]范围的θ – t数据,确定土壤水分扩散率,结果表明,土壤水分扩散率计算结果的决定系数均大于0.990 0,说明临界含水率θlim对土壤水分扩散率结果的影响较小。
3) 与现有确定土壤水分扩散率的方法进行对比,当分析θ – x数据时,迭代法与现有方法的的结果相近,均能得到精度较高的结果;当分析θ – t数据时,本文方法能通过确定后的参数计算出全含水率范围内的土壤水分扩散率,且在低含水率时结果与解析–修正法相近,说明本文方法可以弥补现有方法难以准确确定高体积含水率区间的土壤水分扩散率的不足,这进一步论证了迭代法的合理性。
| [1] |
Kargas G, Londra P, Kerkides P. Investigation of the flux–concentration relation for horizontal flow in soils[J]. Water, 2019, 11(12): 2442 DOI:10.3390/w11122442 (  0) 0) |
| [2] |
鲁建荣, 李云良, 谭志强, 等. 植物根系对土壤水力参数影响的定量研究综述[J]. 土壤学报, 2023, 60(4): 939-952 (  0) 0) |
| [3] |
Berardi M, Difonzo F V, Pellegrino S F. A numerical method for a nonlocal form of Richards' equation based on peridynamic theory[J]. Computers & Mathematics with Applications, 2023, 143: 23-32 (  0) 0) |
| [4] |
Chali A K N, Hashemi S R, Akbarpour A. Numerical solution of the Richards equation in unsaturated soil using the meshless Petrov–Galerkin method[J]. Applied Water Science, 2023, 13(5): 119 DOI:10.1007/s13201-023-01911-8 (  0) 0) |
| [5] |
Su L J, Wang J, Qin X Q, et al. Approximate solution of a one-dimensional soil water infiltration equation based on the Brooks-Corey model[J]. Geoderma, 2017, 297: 28-37 DOI:10.1016/j.geoderma.2017.02.026 (  0) 0) |
| [6] |
Li J W, Jin H, Wang C L, et al. A new method of estimating soil water diffusivity based on variation in the wetting front position and on the principle of stationary action[J]. Journal of Hydrology, 2022, 612: 128290 DOI:10.1016/j.jhydrol.2022.128290 (  0) 0) |
| [7] |
单鱼洋, 马晨光, 王全九, 等. 羧甲基纤维素钠对壤砂土水分运动及水力参数的影响[J]. 土壤学报, 2022, 59(5): 1349-1358 (  0) 0) |
| [8] |
高小龙, 王幼奇, 白一茹, 等. 脱硫石膏对盐碱土一维水平吸渗特征及水分运动参数的影响[J]. 水土保持学报, 2022, 36(3): 100-106 (  0) 0) |
| [9] |
李一博. 二维吸渗与入渗条件下土壤水力特性参数反演方法研究[D]. 杨凌: 西北农林科技大学, 2018.
(  0) 0) |
| [10] |
Gardner W R. Calculation of capillary conductivity from pressure plate outflow data[J]. Soil Science Society of America Journal, 1956, 20(3): 317-320 DOI:10.2136/sssaj1956.03615995002000030006x (  0) 0) |
| [11] |
陈效民. 应用一次出流法结合SFIT模型对土壤水力性质的研究[J]. 土壤学报, 1994, 31(2): 214-219 (  0) 0) |
| [12] |
李奇, 陈文娟, 石文豪, 等. 基于单一和集合土壤转换函数模型对土壤含水量的模拟性能分析[J]. 土壤, 2023, 55(3): 658-670 DOI:10.13758/j.cnki.tr.2023.03.024 (  0) 0) |
| [13] |
Vrugt J A, Bouten W, Weerts A H. Information content of data for identifying soil hydraulic parameters from outflow experiments[J]. Soil Science Society of America Journal, 2001, 65(1): 19-27 DOI:10.2136/sssaj2001.65119x (  0) 0) |
| [14] |
张俊, 徐绍辉, 刘建立, 等. 土壤水力性质参数估计的响应界面和敏感度分析[J]. 水利学报, 2005, 36(4): 445-451 (  0) 0) |
| [15] |
Toorman A F, Wierenga P J, Hills R G. Parameter estimation of hydraulic properties from one-step outflow data[J]. Water Resources Research, 1992, 28(11): 3021-3028 DOI:10.1029/92WR01272 (  0) 0) |
| [16] |
Jing Y Y, Li T L, Zhu X J, et al. Parameter sensitivity analysis of sewage irrigation infiltration process in sandy clay with HYDRUS-1D simulation[J]. IOP Conference Series: Earth and Environmental Science, 2021, 621(1): 012073 DOI:10.1088/1755-1315/621/1/012073 (  0) 0) |
| [17] |
Twarakavi N K C, Šimůnek J, Schaap M G. Development of pedotransfer functions for estimation of soil hydraulic parameters using support vector machines[J]. Soil Science Society of America Journal, 2009, 73(5): 1443-1452 DOI:10.2136/sssaj2008.0021 (  0) 0) |
| [18] |
Kool J B, Parker J C, van Genuchten M T. Determining soil hydraulic properties from one-step outflow experiments by parameter estimation: Ⅰ. theory and numerical studies[J]. Soil Science Society of America Journal, 1985, 49(6): 1348-1354 DOI:10.2136/sssaj1985.03615995004900060004x (  0) 0) |
| [19] |
Bruce R R, Klute A. The measurement of soil moisture diffusivity[J]. Soil Science Society of America Journal, 1956, 20(4): 458-462 DOI:10.2136/sssaj1956.03615995002000040004x (  0) 0) |
| [20] |
孙志祥, 崔俊芳, 杨汝馨, 等. 横断山区森林土壤饱和导水率传递函数的评价与构建研究[J]. 土壤, 2022, 54(3): 594-601 DOI:10.13758/j.cnki.tr.2022.03.021 (  0) 0) |
| [21] |
甘永德, 胡顺军, 陈秀龙. 土壤盐分对土壤水分扩散率的影响[J]. 水土保持通报, 2010, 30(6): 56-59 (  0) 0) |
| [22] |
郭全恩, 南丽丽, 李保国, 等. 灌溉水盐分组成对土壤水盐迁移参数的影响[J]. 农业工程学报, 2017, 33(23): 123-128 (  0) 0) |
| [23] |
姚淑霞, 赵传成, 张铜会. 科尔沁沙地土壤水分扩散率比较研究[J]. 土壤通报, 2014, 45(3): 595-600 (  0) 0) |
| [24] |
Evangelides C, Arampatzis G, Tzimopoulos C. Estimation of soil moisture profile and diffusivity using simple laboratory procedures[J]. Soil Science, 2010, 175(3): 118-127 DOI:10.1097/SS.0b013e3181d53bb6 (  0) 0) |
| [25] |
Villarreal R, Lozano L A, Melani E M, et al. Diffusivity and sorptivity determination at different soil water contents from horizontal infiltration[J]. Geoderma, 2019, 338: 88-96 DOI:10.1016/j.geoderma.2018.11.045 (  0) 0) |
| [26] |
帅嘉伟, 龙平, 胡世丽, 等. 基于水平吸渗确定土壤水分扩散率的解析-修正法[J]. 农业工程学报, 2022, 38(2): 67-75 (  0) 0) |
| [27] |
Carsel R F, Parrish R S. Developing joint probability distributions of soil water retention characteristics[J]. Water Resources Research, 1988, 24(5): 755-769 (  0) 0) |
| [28] |
(美)Ning Lu(卢宁), (美)William J. Likos. 韦昌富, 侯龙, 等译. 非饱和土力学[M]. 北京: 高等教育出版社, 2012.
(  0) 0) |
| [29] |
Ma D H, Zhang J B, Lai J B, et al. An improved method for determining Brooks–Corey model parameters from horizontal absorption[J]. Geoderma, 2016, 263: 122-131 (  0) 0) |
| [30] |
Espejo A, Giráldez J V, Vanderlinden K, et al. A method for estimating soil water diffusivity from moisture profiles and its application across an experimental catchment[J]. Journal of Hydrology, 2014, 516: 161-168 (  0) 0) |
| [31] |
雷志栋. 土壤水动力学[M].
清华大学出版社, 北京, 1988
(  0) 0) |
2. Jiangxi Provincial Key Laboratory of Environmental Geotechnical and Engineering Disaster Control, Ganzhou, Jiangxi 341000, China
 2024, Vol. 56
2024, Vol. 56


