2. 中国科学院大学, 北京 100049;
3. 鹰潭农田生态系统国家野外科学观测研究站(中国科学院南京土壤研究所), 江西鹰潭 335000
土壤容重指在自然状态下单位体积原状土壤的烘干质量,表征土壤的密实程度[1]。土壤容重空间分布是土壤性状改良、土壤养分储量及污染物环境容量等研究的重要基础数据,对耕地地力提升、土壤养分管理及环境治理具有重要的意义[2],但其空间分布受多重结构因素及随机因素的影响[3],预测精度严重受限。
土壤容重空间预测以往多采用基于样点监测数据的地统计方法[4]。其中,普通克里格方法是基于给定样本得到区域化变量的结构信息,联系待推测点有限邻域内的样本数据,对待推测点进行的无偏最优估计,并给出推测方差[5-6]。此外,为进一步提升空间预测精度,也有方法充分考虑了土壤容重与其他属性之间的相关性,通过建立交叉协方差函数进行局部估计,如协同克里格方法[7]。但地统计方法受样点均一性及样点密度影响较大[8],仅考虑各土壤属性之间线性关系,权重强弱取舍存在缺陷[9],空间变异性是否符合内蕴假设尚不清楚[10],且预测精度仍需提升[11]。
目前,机器学习因具有优秀的非线性关系捕捉及高维特征处理能力,成为土壤容重空间预测的热门方法[12]。李民赞等[13]基于集成模型,利用土壤属性纹理特征对土壤容重进行实时预测,得到的容重平均绝对误差(Mean average error, MAE)为0.04 g/cm3,满足田块尺度上精准、快速空间预测要求。在区域尺度上,卢宏亮等[14]基于随机森林(Random forest, RF)算法对安徽省土壤容重的预测精度R2为0.22,狄晓双[15]基于BP神经网络对新疆草地土壤容重的预测精度R2为0.59,表明机器学习方法对土壤容重空间预测行之有效,但因研究区域及选取环境特征指标差异,导致预测精度存在明显差异。Hateffard等[16]还对比了RF、多元线性回归(Multiple linear regression, MLR)、支持向量机(Support vector machine, SVM)、人工神经网络(Articicial neural network, ANN)4种方法对土壤容重的预测效果,表明RF预测方法效果最好,特别在样点数量严重受限条件下。Hengl等[17]基于公开数据库对非洲土壤属性进行空间预测时发现,RF比MLR方法具有更高预测精度,而RF建模成功关键在于输入特征变量的优选,因为一些看似相关的变量对模型预测精度会产生负面影响[18]。
特征变量筛选方法常分为过滤、封装、嵌入和集合4类[19]。其中,过滤法和集合法,常依据特征变量对目标变量的影响程度进行筛选,如灰色关联理论[20]、相关性选择[21]、重要性评价[22-23]等。封装法,如递归特征消除法(Recursive feature elimination, RFE),是一种最大间隔原理的序列后向选择算法,每次剔除一个排序准则分数最小变量,直到获得符合规则要求的特征变量集[24]。张柄华等[25]使用RFE算法对多源遥感影像特征进行筛选,特征数量减少34.5%,提升运算效率的同时也使藏东南土地覆被RF分类整体精度略有提升。常见的特征变量变换嵌入方法,如通过主成分分析(Principal component analysis, PCA)获得新的正交特征[26]、一阶微分变换去除噪声[27]等。但目前将特征筛选与变换嵌入相结合,关注特征之间非线性信息提取的研究极少。姚凯丰等[28]则使用多项式特征扩增方法(Polynomial feature expansion, PFE)对特征变量进行变换,根据SVM的留一错误率,剔除权重较小的特征,有效提高了分类器泛化能力,使四川观音场油气井分类预测误差降低50%。但这种特征变换扩增与筛选相结合的方法,对土壤容重空间预测精度提升是否行之有效,如何以此进一步提升其预测精度,有待进一步研究。
为此,本研究以江西省鹰潭市为研究区,基于样点表层土壤容重调查数据,通过提取影响土壤容重的4类环境因子,包括土地利用[29]、地形因子[30]、气候因子[31]和遥感光谱及指数[32],尝试创建并运用特征变量多重扩增与筛选方法,构建最优特征集,建立RF高精度空间预测模型,揭示研究区土壤容重的空间分布特征,以为充分发挥机器学习方法处理大数据优势[33]、提升数字土壤制图精度及质量提供新思路。
1 材料与方法 1.1 研究区概况鹰潭市(116°41′E ~ 117°30′E,27°35′N ~ 28°41′N)位于江西省东北部,信江中下游,地处武夷山脉与鄱阳湖平原过渡的交接地带,北部连接怀玉山脉,南部连接武夷山脉,中部为信江盆地。区域内最高点海拔1 483 m,最低点–84 m,平均40 m。气候类型为亚热带湿润季风气候,年均温18 ℃,年均降水量1 750 mm,全年无霜期262 d。鹰潭市现有余江区、月湖区和贵溪市3个辖区,总面积约3 520 km2。土地利用类型包括耕地、林地、园地、草地、工矿仓储用地、住宅用地、水域及水利设施用地、交通用地及其他土地。其中,林地面积约占54.6%,主要分布在鹰潭市南北两端;耕地面积约占25.6%,主要分布于中部信江盆地,沿信江向南北方向辐射,是江西省重要商品粮基地。市内矿产资源丰富,也是全国最大铜冶炼、铜加工基地及重要的铜消费区[34]。
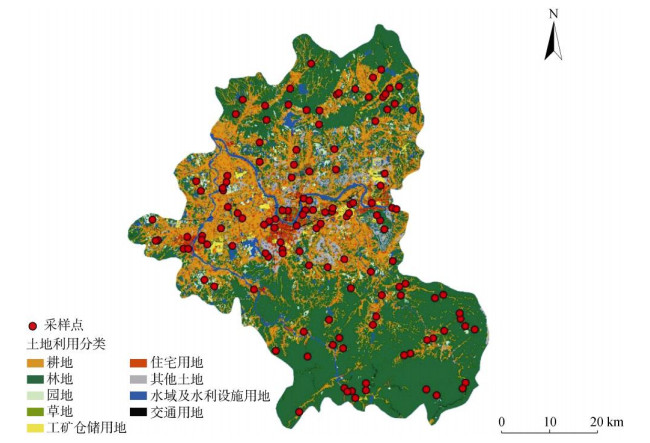
1.2 样点布设及容重数据获取2021年12月,考虑土地利用及土壤类型空间分布特征基础上,布设131个调查样点(图 1)。其中,耕地、林地、草地、工矿仓储用地、园地的样点数分别约占48.1%、33.6%、7.6%、4.6%、2.3%,其他土地包括裸土地、空闲地和设施农用地,样点数共占3.8%。每个采样点使用环刀法采集0 ~ 20 cm土壤容重平行样品3个,以均值作为该样点土壤容重数值。采用环刀法测定土壤容重[35]。
|
图 1 研究区土地利用与土壤样点分布 Fig. 1 Distribution of land use types and soil sample sites in study area |
以2020年9月至2021年6月空间分辨率为10 m、云量小于0.05% 的Sentinel-2 Level-2A遥感影像作为环境协变量数据源(https://sentinel.esa.int/web/sentinel/user-guides/sentinel-2-msi/processing-levels/level-2)。
首先,参照GB/T 21010—2017《土地利用现状分类》标准[36]进行目视解译,获得土地利用类型矢量数据。利用ArcGIS空间连接功能获得样点处的土地利用类型及邻接指定区域面积变量,指定区域包括住宅用地、工矿仓储用地和空闲地;采用近邻分析工具获得样点距建筑、城市建筑、农村建筑距离和距河流、公路距离共5个距离变量。
其次,利用Google Earth Engine(GEE)工具提取单波段数据(B2、B3、B4、B5、B6、B7、B8A、B8、B11、B12)和15种遥感指数数据,包括亮度指数(BI)、颜色指数(CI)、差值植被指数(DVI)、绿光归一化差值植被指数(GNDV)、红外植被百分比指数(IPVI)、改进红边叶绿素指数(IRECI)、修正的叶绿素吸收反射指数(MCAR)、陆地叶绿素指数(MTCI)、归一化差异指数(NDI)、植物衰老反射率指数(PSSR)、红边位置指数(REIPI)、红光指数(RI)、比值植被指数(RVI)、土壤背景指数(SBI)、转换归一化植被指数(TNDVI);再利用SNAP 9.0.0工具计算10种纹理指数,包括最大概率指数(MAX)、角二阶矩指数(ASM)、对比度指数(Contrast)、不相似性指数(Dissimilar)、能量指数(Energy)、熵指数(Entropy)、相关性指数(GLCMCorrel)、均值指数(GLCMMean)、方差指数(GLCMVarian)、均匀性指数(Homogeneit)。
同时,以采样前后3个月内同时相Sentinel-1 SAR GRD为数据源(https://sentinel.esa.int/web/sentinel/user-guides/sentinel-1-sar/),利用GEE工具提取后向散射系数(VV和HV);以同时相USGS Landsat 8 level 2、collection2、Tier1为数据源(https://www.usgs.gov/landsat-missions/landsat-collection-2-level-2-science-products),提取最大归一化植被指数(maxNDVI)、最大增强植被指数(maxEVI)和土壤调节植被指数(MSAVI)以及数字高程模型(DEM);进而利用SAGA GIS 8.3.0计算14种地形因子,如坡度(Slope)、坡向(Aspect)、坡长(SL)、平面曲率(Plan_cur)、剖面曲率(Prof_cur)、地形位置指数(TPI)、地形湿度指数(TWI)、地表粗糙指数(TRI)、谷深(VallyDepth)、流域面积(CatchmentA)、山体阴影(Hillshader)、水流强度指数(SPI)、多尺度山谷平坦指数(MRVBF)、多尺度山顶平坦指数(MRRTF)。
另外,气候因子来自国家地球系统科学数据中心(http://www.geodata.cn),利用ArcGIS工具提取2015—2020年年均温(MAT)和年均降水量(MAP)数据。
最后,利用ArcGIS 10.8将所有环境协变量图层投影转换至同一大地坐标系,并以30 m栅格分辨率进行数据重采样。
1.4 特征变量多重扩增与筛选路径首先,将提取的66个原始环境协变量标记为特征集S1;其次,利用SPSS 26.0软件对特征集S1进行PCA分析[37],以特征值大于1为标准,提取主成分特征,标记为特征集S2,并将其与S1的组合标记为特征集S3;接着,对特征集S3(79个特征变量)进行Pearson相关分析[38],根据显著性值P < 0.05,筛选出高相关性特征变量,标记为特征集S4。
交叉验证递归筛选(Recursive feature elimination with cross-validation,RFECV)是一种结合递归特征消除和交叉验证思想、自动选择特征变量的RFE方法,可给出体现模型性能最佳的特征组合和数量[39]。RFECV通常利用指定模型(如SVM、RF)对当前特征子集进行变量重要性评价,同时利用指定方法(如十折交叉验证、留一交叉验证)进行模型性能评价,删除当前特征子集中最不重要特征变量,从而获得新特征子集;通过循环不断评价、选择,直到获得最优特征子集,使得模型性能达到最优。本研究使用Python中的RFECV函数[40]对特征集S3进行首次RFECV筛选,并获得特征集S5。
多项式特征扩增(Polynomial feature expansion,PFE)是一种对数据进行高阶组合的方法,通过对特征进行高阶多项式映射扩增特征变量,从而捕捉特征之间更多非线性关系,例如二维特征(X1,X2)T
最后,对特征集S6再次进行RFECV筛选,获得最终参与建模的最优特征变量集合,标记为S7。
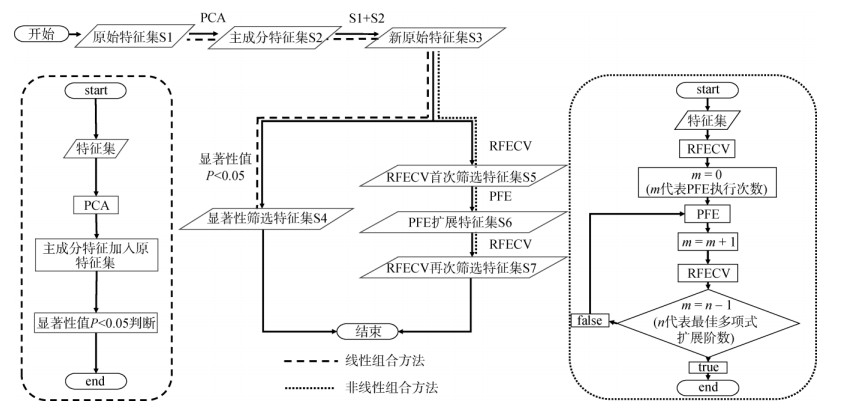
特征变量多重扩增与筛选路径如图 2所示。
|
图 2 特征变量多重扩增与筛选路径 Fig. 2 Roadmap for feature expanding and screening |
随机森林模型(Random forest, RF)是由Breiman[41]提出的基于决策树的集成学习技术,每棵决策树代表一个分类器,通过对多个分类器的输出结果进行投票或取平均值,实现分类或回归预测。RF实现回归预测步骤为:①采用重采样(bootstrap)有放回的方法选择n个样本作为训练集,构建n棵回归树(ntree),每次未被选中的袋外样本(OOB)构成测试集,用于验证模型的泛化能力;②从特征变量中抽取m个解释变量(mtry),按照OOB预测误差最小原则确定mtry的值,由此决定每棵决策树使用的特征数量;③将所有决策树的预测值取平均,得到RF最终回归预测结果。本研究使用Python中的RandomizedSearch与GridSearchCV函数确定RF参数[42]。
1.6 模型验证与精度评价使用Python中留一交叉验证(LeaveOneOut)函数对模型精度进行评价。已知原始数据有N(N=131)个样点,选择(N–1)个样点作为训练样本,将每个样点视为独立的验证样本,经过N次模型运行后获得N个预测结果,对应于样本真实值,计算均方根误差(RMSE)及决定系数(R2),RMSE越小、R2越接近1,表明预测精度越高[43]。
1.7 土壤容重空间分布制图使用Python中gdal函数结合上述RF建模过程,对研究区土壤容重空间分布进行回归预测制图。为比较和展现基于本文特征变量多重扩展与筛选的RF方法预测优势,利用ArcGIS 10.8中Geostatistical Wizard模块和最优变量集,进行土壤容重协同克里格插值(COK)[44]制图。空间分辨率均为30 m×30 m。
2 结果与讨论 2.1 土壤容重样点统计特征研究区样点土壤容重变化范围为0.67 ~ 1.72 g/cm3,平均值为1.22 g/cm3,标准差为0.22 g/cm3,变异系数为0.18,数值相对集中且变化范围较小,数据相对离散程度较低;偏度为0.32,数据分布向右偏,峰度为–0.51,数据分布有平坦峰度(表 1)。
|
|
表 1 不同土地利用类型土壤容重基本统计特征 Table 1 Statistical characteristics of soil bulk densities under different land use types |
不同土地利用类型中,人为活动频繁的工矿仓储用地土壤容重平均值最高为1.45 g/cm3,原因是该类土地存在改造、挖掘填埋等情况,特别是机械碾压导致土壤紧实,通气透水性减弱,土壤容重偏高[45];耕地土壤容重平均值最低,为1.14 g/cm3,这可能是翻耕等农业活动减轻土壤压实,增加土壤通气性,同时施肥和秸秆还田等增加土壤有机质,有利于土壤团粒结构形成,改善土壤质地,增加土壤孔隙度。
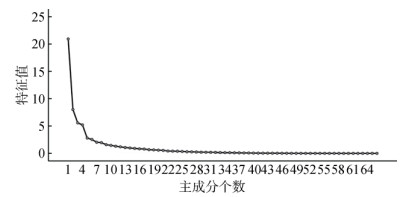
2.2 多重扩增与筛选特征集变化特征 2.2.1 主成分变量扩增原始特征变量集S1的PCA分析表明,前13个主成分变量总解释方差达84.43%,而前14个主成分总解释方差达85.92%(表 2),但第14个主成分起始特征值小于1,该因子包含信息不足以证明其应该保留[46]。主成分碎石图(图 3)显示,当提取的主成分为13个时,折线由陡峭变得平稳。经综合考虑,本研究提取13个主成分变量,分别标记为PCA1 ~ PCA13,在此首次实现线性过程的变量扩增。
|
|
表 2 特征变量总方差解释表 Table 2 Explanatory table for total variance of characteristic variables |
|
图 3 环境协变量主成分碎石图 Fig. 3 Principal components crushed stone figure of environmental covariates |
包含66个原始特征的变量集S1、包含13个PCA新增特征的变量集S2及其组合包含79个特征的变量集S3 (PCA扩增特征集),分别参与RF土壤容重预测的精度R2为0.351、0.112和0.354,基于特征集S3的RF预测精度仅略有提高。
与原始特征变量集S1相比,基于PCA新增特征集S2的预测精度降低,原因在于PCA方法通过线性组合提取能够最大程度保留原始数据方差的新特征,将原始特征映射到主成分空间会导致信息损失,某些与目标变量相关但方差较小的特征被忽略[47]。而PCA扩增特征集S3维度比特征集S1增加约19.7%,引入了与目标变量相关信息,预测精度提高约0.85%。
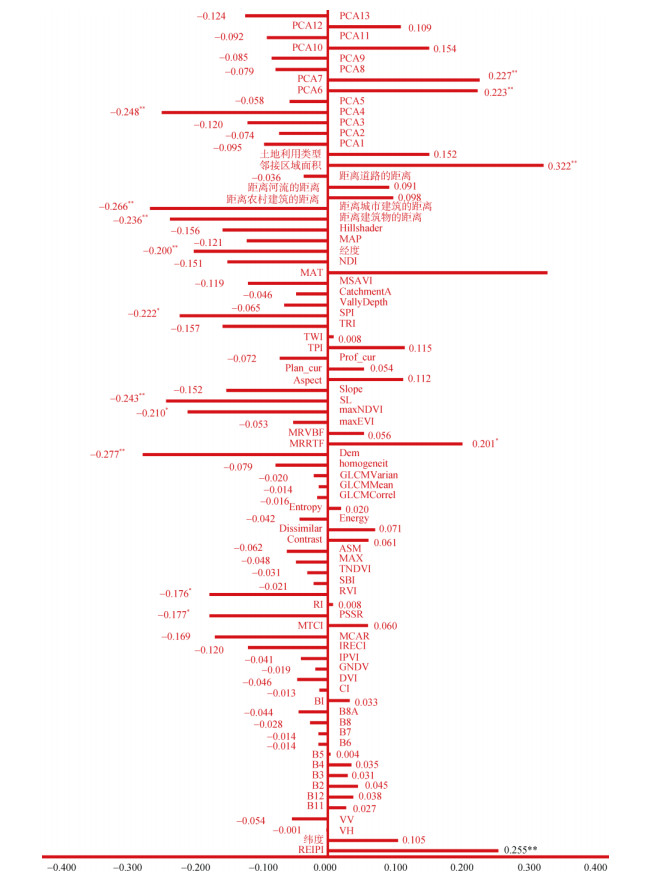
2.2.2 线性筛选通过新原始特征集(PCA扩增特征集,S3)变量与土壤容重之间的Pearson线性相关性分析(图 4),对特征集S3进行降维,其中显著性P < 0.05的变量有RVI、PSSR、经度、MRRTF、maxNDVI、SPI、PCA6、PCA7、距离建筑物的距离、SL、PCA4、REIPI、距离城市建筑的距离、Dem、邻接区域面积和MAT共16个变量,由此,获得新特征集S4。基于特征集S4,RF对土壤容重的预测精度R2为0.344,虽然较特征集S3减少了约79.7% 输入变量,但预测精度R2却低于特征集S3 (R2=0.351),降低约2.8%,与提升空间预测精度目标背道而驰。
|
(REIPI,红边位置指数;VH、VV,后向散射系数;B2、B3、B4、B5、B6、B7、B8、B8A、B11、B12,Sentinel-2的B2、B3、B4、B5、B6、B7、B8、B8A、B11、B12单波段;BI,亮度指数;CI,颜色指数;DVI,差值植被指数;GNDV,绿光归一化差值植被指数;IPVI,红外植被百分比指数;IRECI,改进红边叶绿素指数;MCAR,修正的叶绿素吸收反射指数;MTCI,陆地叶绿素指数;PSSR,颜料特定的简单比率;RI,红光指数;RVI,比值植被指数;SBI,土壤背景指数;TNDVI转换归一化植被指数;MAX,最大概率指数;ASM,角二阶矩指数;Contrast,对比指数;Dissimilar,不相似性指数;Energy,能量指数;Entropy,熵指数;GLCMCorrel,灰度共生矩阵的相关性指数;GLCMMean,灰度共生矩阵的均值指数;GLCMVarian,灰度共生矩阵的方差指数;homogeneit,均匀性指数;Dem,数字高程模型;MRRTF,多尺度山顶平坦指数;MRVBF,多尺度山谷平坦指数;maxEVI,最大增强植被指数;maxNDVI,最大归一化植被指数;SL坡长;Slope,坡度;Aspect,坡向;Plan_cur,平面曲率;Prof_cur,剖面曲率;TPI,地形位置指数;TWI,地形湿度指数;TRI,地表粗糙指数;SPI,水流强度指数;Vally Depth,谷深;Catchment A,流域面积;MSAVI,土壤调节植被指数;MAT,年均温;NDI,归一化差异指数;MAP,年降水量;Hillshader,山体阴影;PCA1~PCA13,主成分1到主成分13。*、**分别表示相关性在P < 0.05、P < 0.01水平显著) 图 4 环境协变量与土壤容重的相关性分析 Fig. 4 Correlation analysis of environmental covariates with soil bulk density |
在指定RF模型和留一交叉验证方法前提下,RFECV方法从特征集S4中初步筛选出的新特征集S5包含4个特征变量,分别为REIPI、MAT、NDI和经度,RF对土壤容重的预测精度R2为0.435,与先前特征集(S1、S2、S3、S4)比较,预测精度均得到明显提升(表 3)。特征集S5代表了RFECV首次筛选结果,对比特征集S3,特征维度降低约94.9%,预测精度提高约22.9%。与线性扩增和线性筛选相比,RFECV方法在RF模型下在特征降维和精度提升两方面均有明显优势[48]。
|
|
表 3 不同特征集的来源和RF预测精度对比 Table 3 Comparison of different feature sets and their RF prediction accuracies |
在特征集S5基础上,尝试1 ~ 6阶扩增的RF预测结果显示,基于2阶的PEF扩增特征集S6的RF预测精度R2最高,为0.442(表 4),表明组合迭代1次就能够使原始特征变换到最佳状态,且比先前所有特征集的预测精度又有了明显提升(表 3)。但PFE通过原始特征间相乘和幂运算提高了特征维度,引入了更多非线性关系,特征维度提升约为特征集S5的4倍,这会导致模型计算开销的增高[49],对RFECV与PFE组合迭代次数也有重要影响,因此需选择最佳多项式阶数。
|
|
表 4 多项式不同阶数特征扩增集的预测精度 Table 4 Prediction accuracies of polynomial feature expansion of different orders attempted |
在2阶PFE扩展特征集S6的基础上再进行RFECV筛选,筛选出3个变量构成新的特征集S7,包括REIPI、REIPI与MAT的乘积、NDI与经度的乘积,其参与RF预测的精度R2最高,为0.469,超出了先前所有特征集的预测精度(表 3)。S6特征集经RFECV再次筛选得出的特征集S7,特征维度降低80.0%,不仅预测精度提高约6.1%,也抑制了特征多项式扩增后的计算成本上升。
总之,通过本研究创建的特征变量多重扩增与筛选路径,对比S7和S3特征集,经非线性扩增和筛选使原始特征维度降低约96.2%,土壤容重RF空间预测精度提高约32.5%,达到预设研究目标。
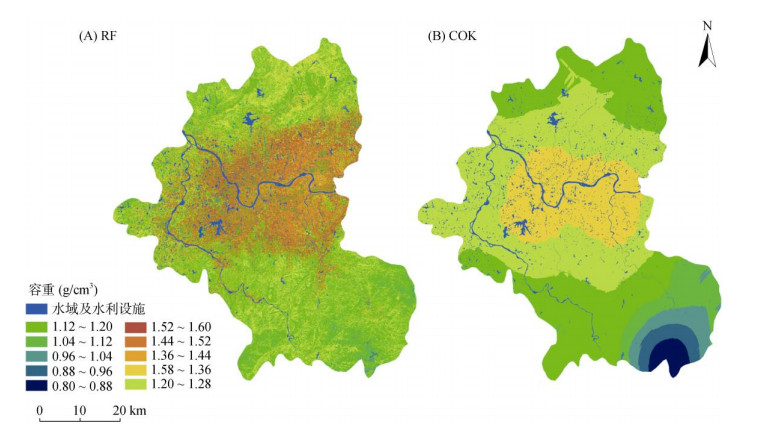
2.3 土壤容重空间预测分布特征将通过多重扩增与筛选方法获得的特征集S7变量(REIPI、REIPI与MAT的乘积、NDI与经度的乘积)分别输入RF模型和COK模型进行土壤容重的空间预测,结果表明,两种方法所展示的土壤容重空间变化趋势具有相似性,即由南北山地到中部盆地土壤容重逐渐升高(图 5),与样点数据空间分布特征一致,原因在于中部地区集中有住宅用地和工矿仓储用地,土壤容重高值点相对集中。此外,邻接域面积代表人为扰动范围和强度,与土壤容重的相关系数为0.322**,有显著正相关性(图 4),也间接验证了研究区中部余江、月湖和贵溪市区一带土壤容重较高的现象。
|
图 5 研究区表层土壤容重空间预测分布 Fig. 5 Results of spatial prediction of top soil bulk density in study area |
COK预测精度R2为0.139,远低于RF模型的预测精度(R2=0.469);COK模型预测值和预测区间均偏小,预测区间仅为0.80 ~ 1.34 g/cm3,而RF模型预测区间拓宽为0.86 ~ 1.57 g/cm3;土壤容重空间预测分布图呈现的微域变异特征,RF模型比COK模型预测效果更为精细。这表明应用多重扩增与筛选方法也需指定模型(如RF)与验证方法(如留一交叉验证)对特征集变量重要性与模型性能进行评价,从而获得与指定模型相对应的最优特征集。基于RF模型进行的空间预测比基于COK模型的预测更具优势,是因为RF组合方法重在数据挖掘,充分考虑环境变量间的非线性关系和交互影响,这再次彰显了机器学习处理大数据的强大能力。
比较各土地利用类型土壤容重的预测结果,发现RF模型对林地预测效果最好(表 5),但对耕地存在高估,对园地、工矿仓储用地存在低估。一方面RF模型为全局最优预测模型,但预测精度R2仅为0.469,总体拟合精度有限;另一方面,耕地及工矿仓储用地集中分布在研究区中部,受人为活动强烈影响,空间变异性更强,且土地利用类型特征未能选取参与建模,局部拟合精度提升不足。尽管如此,各土地利用类型样点的平均预测值总体偏差均小于10%(表 5),预测结果仍可接受。
|
|
表 5 不同土地利用类型采样点土壤容重RF预测结果对比 Table 5 Comparisons of RF predictions for soil bulk density of sampling points under different land uses |
基于多重扩增与筛选方法获得的最优特征集S7,土壤容重RF空间预测取得了满意效果,与原始特征集S1比较,特征维度降低约95%,RF预测精度提升约34%。这种特征多重扩增与筛选方法与RF模型组合,充分利用了非线性组合优势,最大限度在降低计算维度的同时提高了预测精度,成为一种经济、高效的特征优化方法。该组合方法重在数据挖掘,考虑环境变量间的非线性关系和交互影响,但变量对土壤容重影响的机理不明确,给特征变量的合理性解释带来了困难,是数据驱动预测的弱点[50]。尽管如此,本文依然尝试从土壤容重空间分布格局角度分析最优特征集S7变量(REIPI、REIPI与MAT的乘积、NDI与经度的乘积)的合理性。
REIPI为红边位置指数,遥感红边指数是表征绿色植物生长状况的重要生化参数[51];NDI为归一化差异指数,其数值变化常用于监测植物生长情况[52],二者的空间变化都可以反映植被覆盖差异。两个植被指数在林区数值较高,与冬季林区植被覆盖度高于农田和城镇的实际情况相符。RF预测图中,河流沿岸土壤容重要高于附近山地土壤容重,是因为山地林区覆盖的枯枝落叶分解后增加了土壤有机物含量,良好的植被条件降低了土壤容重[53]。
MAT为年均气温,该指数的空间分布反映了不同区域的温度差异,样点土壤容重与MAT相关系数为0.328,相关性极显著(P < 0.01)。MAT高导致地区土壤水分蒸发量大,热量累积也会使土壤干燥收缩,进而导致土壤容重增大[54]。
经度代表了土壤容重东西走向的综合空间差异,样点容重与经度的相关系数为–0.2,相关性显著(P < 0.05)。根据相关系数分析,土壤容重预测值东部应该低于西部,但RF预测图中并没有明显的横向差异。经度与NDI指数的乘积成为提高RF预测精度的重要特征,反映二者对土壤容重有着非直观的交互影响,达到了本研究提取多个特征之间非线性信息的目的。
总之,本研究建立的最优特征集S7,不是通过某个筛选方法能直接获取的,而是基于线性与非线性多种组合方式,通过对原始特征的多重扩增与筛选才能取得的。这种特征变量多重扩增与筛选方法,不仅有效降低了特征维度与运算成本,而且显著提升了机器学习方法(RF)的空间预测精度,为提升数字土壤制图精度及质量增添了新途径。
3 结论本研究结合PFE和RFECV方法,基于RF模型对多源环境数据进行特征变量多重扩增与筛选,结果表明,该方法能经济、高效地优选出具有最佳预测精度的特征组合,相比传统线性特征筛选方法,进一步提高了研究区内表层土壤容重的预测精度,更充分挖掘了土壤与环境特征之间的非线性关系,为其他土壤属性高精度预测及特征前处理提供了新途径和成功案例。
| [1] |
邵明安, 王全九, 黄明斌. 土壤物理学[M].
高等教育出版社, 北京, 2006
(  0) 0) |
| [2] |
Kosmas C, Gerontidis S, Marathianou M. The effect of land use change on soils and vegetation over various lithological formations on Lesvos (Greece)[J]. CATENA, 2000, 40(1): 51-68 DOI:10.1016/S0341-8162(99)00064-8 (  0) 0) |
| [3] |
Li S, Li Q Q, Wang C Q, et al. Spatial variability of soil bulk density and its controlling factors in an agricultural intensive area of Chengdu Plain, Southwest China[J]. Journal of Integrative Agriculture, 2019, 18(2): 290-300 DOI:10.1016/S2095-3119(18)61930-6 (  0) 0) |
| [4] |
巫振富, 赵彦锋, 程道全, 等. 样点数量与空间分布对县域尺度土壤属性空间预测效果的影响[J]. 土壤学报, 2019, 56(6): 1321-1335 (  0) 0) |
| [5] |
朱阿兴, 杨琳, 樊乃卿, 等. 数字土壤制图研究综述与展望[J]. 地理科学进展, 2018, 37(1): 66-78 (  0) 0) |
| [6] |
潘宗涛, 陈志强, 陈志彪. 朱溪流域土壤容重空间分异与地形和土地利用的关系[J]. 水土保持通报, 2018, 38(3): 263–268, 2 (  0) 0) |
| [7] |
石淑芹, 曹祺文, 李正国, 等. 区域尺度土壤养分的协同克里格与普通克里格估值研究[J]. 干旱区资源与环境, 2014, 28(5): 109-114 (  0) 0) |
| [8] |
潘成忠, 上官周平. 土壤空间变异性研究评述[J]. 生态环境, 2003, 12(3): 371-375 (  0) 0) |
| [9] |
郭龙, 张海涛, 陈家赢, 等. 基于协同克里格插值和地理加权回归模型的土壤属性空间预测比较[J]. 土壤学报, 2012, 49(5): 1037-1042 (  0) 0) |
| [10] |
秦耀东. 土壤空间变异研究中的定量分析[J]. 地球科学进展, 1992, 7(1): 44-49 (  0) 0) |
| [11] |
连纲, 郭旭东, 傅伯杰, 等. 基于环境相关法和地统计学的土壤属性空间分布预测[J]. 农业工程学报, 2009, 25(7): 237-242 (  0) 0) |
| [12] |
刘付程, 郭衍游, 闫晓波. 土壤属性空间预测的广义回归神经网络方法研究[J]. 淮海工学院学报(自然科学版), 2008, 17(1): 68-71 (  0) 0) |
| [13] |
李民赞, 任新建, 杨玮, 等. 基于树莓派的农田表土层土壤容重检测系统研究[J]. 农业机械学报, 2021, 52(S1): 329–335, 376 (  0) 0) |
| [14] |
卢宏亮, 赵明松, 刘斌寅, 等. 基于随机森林模型的安徽省土壤属性空间分布预测[J]. 土壤, 2019, 51(3): 602-608 DOI:10.13758/j.cnki.tr.2019.03.025 (  0) 0) |
| [15] |
狄晓双. 新疆主要草地土壤容重预测模型构建[D]. 乌鲁木齐: 新疆农业大学, 2021.
(  0) 0) |
| [16] |
Hateffard F, Szatmári G, Novák T J. Applicability of machine learning models for predicting soil organic carbon content and bulk density under different soil conditions[J]. Soil Science Annual, 2023, 74(1): 165879 (  0) 0) |
| [17] |
Hengl T, Heuvelink G B M, Kempen B, et al. Mapping soil properties of Africa at 250 m resolution: Random forests significantly improve current predictions[J]. PLoS One, 2015, 10(6): e0125814 DOI:10.1371/journal.pone.0125814 (  0) 0) |
| [18] |
Archer K J, Kimes R V. Empirical characterization of random forest variable importance measures[J]. Computational Statistics & Data Analysis, 2008, 52(4): 2249-2260 (  0) 0) |
| [19] |
Chen Y, Ma L X, Yu D S, et al. Comparison of feature selection methods for mapping soil organic matter in subtropical restored forests[J]. Ecological Indicators, 2022, 135: 108545 DOI:10.1016/j.ecolind.2022.108545 (  0) 0) |
| [20] |
郭李娜, 樊贵盛. 基于灰色理论—BP神经网络方法的表层土壤容重预测[J]. 节水灌溉, 2018(2): 93-97 (  0) 0) |
| [21] |
刘丽媛, 郑向群, 张春雪, 等. 稻田有机肥配施的土壤环境效应评价指标体系构建[J]. 农业资源与环境学报, 2022, 39(1): 129-138 (  0) 0) |
| [22] |
张东彦, 杨玉莹, 黄林生, 等. 结合Sentinel-2影像和特征优选模型提取大豆种植区[J]. 农业工程学报, 2021, 37(9): 110-119 (  0) 0) |
| [23] |
顾永昇, 丁建丽, 韩礼敬, 等. 基于多源环境变量的渭–库绿洲土壤颗粒含量预测研究[J]. 土壤, 2023, 55(2): 426-432 DOI:10.13758/j.cnki.tr.2023.02.024 (  0) 0) |
| [24] |
林俊, 许露, 刘龙. 基于SVM-RFE-BPSO算法的特征选择方法[J]. 小型微型计算机系统, 2015, 36(8): 1865-1868 (  0) 0) |
| [25] |
张炳华, 张镱锂, 谷昌军, 等. 基于随机森林与特征选择的藏东南土地覆被分类方法及精度评价[J]. 地理科学, 2023, 43(3): 388-397 (  0) 0) |
| [26] |
聂红梅, 杨联安, 李新尧, 等. 基于PCA-SVR的冬小麦土壤水分预测[J]. 土壤, 2018, 50(4): 812-818 (  0) 0) |
| [27] |
何挺, 王静, 林宗坚, 等. 土壤有机质光谱特征研究[J]. 武汉大学学报(信息科学版), 2006, 31(11): 975-979 (  0) 0) |
| [28] |
姚凯丰, 陆文凯, 丁文龙, 等. 一种基于SVM特征选择的油气预测方法[J]. 天然气工业, 2004, 24(7): 36–38, 134 (  0) 0) |
| [29] |
邱倩倩, 张卓栋, 孙传龙, 等. 锡林郭勒草地景观系统土壤容重空间变异及其与风蚀的关系[J]. 水土保持通报, 2016, 36(6): 58–62, 66 (  0) 0) |
| [30] |
冯强, 段宝玲, 姜硕. 小流域尺度土壤容重及其影响因素的空间变异[J]. 山西农业大学学报(自然科学版), 2013, 200(1): 99-107 (  0) 0) |
| [31] |
Aitkenhead M J, Coull M, Towers W, et al. Prediction of soil characteristics and colour using data from the National Soils Inventory of Scotland[J]. Geoderma, 2013, 200(1): 99-107 (  0) 0) |
| [32] |
Pittman R, Hu B. Estimation of soil bulk density and carbon using multi-source remotely sensed data[J]. ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2020, 3: 541-548 (  0) 0) |
| [33] |
Salehi Hikouei I, Kim S S, Mishra D R. Machine-learning classification of soil bulk density in salt marsh environments[J]. Sensors, 2021, 21(13): 4408 (  0) 0) |
| [34] |
汪容基, 赵小敏, 郭熙, 等. "三生空间" 视角下的土地利用转型与生态环境效应研究——以江西省鹰潭市为例[J]. 江西农业大学学报, 2021, 43(3): 681-693 (  0) 0) |
| [35] |
江胜国. 国内土壤容重测定方法综述[J]. 湖北农业科学, 2019, 58(S2): 82–86, 91 (  0) 0) |
| [36] |
国家质量监督检验检疫总局, 中国国家标准化管理委员会. 土地利用现状分类: GB/T 21010—2017[S]. 北京: 中国标准出版社, 2017.
(  0) 0) |
| [37] |
徐夕博, 吕建树, 吴泉源, 等. 基于PCA-MLR和PCA-BPN的莱州湾南岸滨海平原土壤有机质高光谱预测研究[J]. 光谱学与光谱分析, 2018, 38(8): 2556-2562 (  0) 0) |
| [38] |
闫政旭, 秦超, 宋刚. 基于Pearson特征选择的随机森林模型股票价格预测[J]. 计算机工程与应用, 2021, 57(15): 286-296 (  0) 0) |
| [39] |
李安琪, 杨琳, 蔡言颜, 等. 基于递归特征消除-随机森林模型的江浙沪农田土壤肥力属性制图[J]. 地理科学, 2024, 44(1): 168-178 (  0) 0) |
| [40] |
李恒凯, 王利娟, 肖松松. 基于多源数据的南方丘陵山地土地利用随机森林分类[J]. 农业工程学报, 2021, 37(7): 244-251 (  0) 0) |
| [41] |
Breiman L. Random forest[J]. Machine Learning, 1999, 45: 1-35 (  0) 0) |
| [42] |
Ordoñez Palacios L E, Bucheli Guerrero V, Ordoñez H. Machine learning for solar resource assessment using satellite images[J]. Energies, 2022, 15(11): 3985 (  0) 0) |
| [43] |
Chai T, Draxler R R. Root mean square error (RMSE) or mean absolute error (MAE)? –Arguments against avoiding RMSE in the literature[J]. Geoscientific Model Development, 2014, 7(3): 1247-1250 (  0) 0) |
| [44] |
Yang Q Y, Luo W Q, Jiang Z C, et al. Improve the prediction of soil bulk density by cokriging with predicted soil water content as auxiliary variable[J]. Journal of Soils and Sediments, 2016, 16(1): 77-84 (  0) 0) |
| [45] |
任婷婷, 王瑄, 孙雪彤, 等. 不同土地利用方式土壤物理性质特征分析[J]. 水土保持学报, 2014, 28(2): 123-126 (  0) 0) |
| [46] |
游家兴. 如何正确运用因子分析法进行综合评价[J]. 统计教育, 2003(5): 10-11 (  0) 0) |
| [47] |
McCaskey S D, Tsui K L. Analysis of dynamic robust design experiments[J]. International Journal of Production Research, 1997, 35(6): 1561-1574 (  0) 0) |
| [48] |
杨珺雯, 张锦水, 朱秀芳, 等. 随机森林在高光谱遥感数据中降维与分类的应用[J]. 北京师范大学学报(自然科学版), 2015, 51(S1): 82-88 (  0) 0) |
| [49] |
王猛, 张新长, 王家耀, 等. 结合随机森林面向对象的森林资源分类[J]. 测绘学报, 2020, 49(2): 235-244 (  0) 0) |
| [50] |
杨倩倩, 靳才溢, 李同文, 等. 数据驱动的定量遥感研究进展与挑战[J]. 遥感学报, 2022, 26(2): 268-285 (  0) 0) |
| [51] |
方灿莹, 王琳, 徐涵秋. 不同植被红边指数在城市草地健康判别中的对比研究[J]. 地球信息科学学报, 2017, 19(10): 1382-1392 (  0) 0) |
| [52] |
Amiri M, Pourghasemi H R. Mapping the NDVI and monitoring of its changes using Google Earth Engine and Sentinel-2 images[M]. Computers in Earth and Environmental Sciences. Amsterdam: Elsevier, 2022: 127–136.
(  0) 0) |
| [53] |
鲍文, 赖奕卡. 湘中红壤丘陵区不同土地利用类型对土壤特性的影响[J]. 中国水土保持, 2011(10): 47–50, 66 (  0) 0) |
| [54] |
乔宇鑫, 朱华忠, 钟华平, 等. 内蒙古地区草地表层土壤容重空间格局分析[J]. 草地学报, 2016, 24(4): 793-801 (  0) 0) |
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Farmland Ecosystem National Field Observation and Research Station (Institute of Soil Science, Chinese Academy of Sciences), Yingtan, Jiangxi 335000, China
 2024, Vol. 56
2024, Vol. 56


