2. 中国科学院南京土壤研究所, 南京 211135;
3. 中国科学院大学, 北京 100049;
4. 中国科学院大学南京学院, 南京 211135
土壤压实是因施加载重、振动或压力使土壤颗粒重新排列,从而导致土壤孔隙度降低、容重增加的过程,主要是由于农业机械进行田间作业时,对土壤表面施加的外力作用造成的[1]。压实会导致土壤结构和物理性状退化、水分渗透能力下降、作物根系生长和吸收养分受阻,从而影响耕地粮食产能[2-3]。
土壤压实的程度可采用容重、孔隙度、土壤强度等土壤物理性质来表征[1],也可通过室内实验测定土壤压实曲线(即荷载压力和土壤孔隙比之间的关系),然后用手工作图法或者参数模型拟合实测曲线[4],计算压缩指数、回弹指数、预固结压力等土壤压实特征参数[5-6],来定量评估土壤的抗压能力、恢复能力和承压极限,指导制定土壤压实的缓解和预防措施等[7-9]。
由于目前仍缺少具有明确物理意义的土壤压实曲线数学模型,土壤学和土力学研究者基于土壤单轴压缩试验[10]数据,提出了多种描述土壤压实曲线的经验模型。如Arvidsson和Keller[11]用四次多项式分析了18种瑞典农田土壤样品的单轴压缩试验数据。Baumgartl和Köck [12]提出用van Genuchten土壤水分特征曲线模型(VG)描述土壤固结过程中的孔隙比变化,并计算了10种土壤的预固结应力,结果表明VG方程可以高精度地模拟样品的体积变化,并可从该方程的导数中推出预固结压力等土壤压实参数。Gregory等[13]采用四次多项式、Logistic方程和Gompertz方程拟合英国农场土壤的单轴压缩试验数据,均取得了较好的拟合效果,其中Gompertz方程效果最佳。霍连飞等[14]采用Gompertz函数拟合了不同含水率和容重下的水稻土压实曲线,效果令人满意。郎林智等[15]采用高斯模型拟合土壤压实曲线,表明Gauss1模型、Gauss2模型拟合程度高,其中的Gauss1模型确定的预固结应力与土工试验方法现行规范较吻合。
采用参数模型拟合实测土壤压实曲线数据、计算土壤压实参数,避免了经典的手绘作图法中人为因素的干扰,得出的结果更加客观可靠。但是在农田土壤的试验数据处理中,选择何种形式的参数模型仍需进一步分析讨论。特别是这些经验性的参数模型的适用性尚未经过系统和全面的验证,在很大程度上制约了土壤压实过程仿真模型的应用。本文基于室内单轴压缩试验数据,将Brooks-Corey、Kosugi、Fredlund-Xing等水分特征曲线模型引入土壤压实曲线研究,通过与来自文献的多种模型对比分析,试图找到适用性广、实用性强的土壤压实曲线参数模型,为农田土壤压实过程的定量化研究提供参考依据。
1 材料与方法 1.1 土壤压实曲线参数模型本文共选择10种经验性的参数模型,包括Brooks-Corey、Kosugi、van Genuchten、Fredlund-Xing 4种土壤水分特征曲线方程,Logistic方程、Gompertz方程2种S型生长曲线模型,三次多项式、四次多项式函数,以及Gauss模型、Harris模型等。各模型的表达式如表 1所示。
|
|
表 1 研究采用的10个土壤压实曲线参数模型 Table 1 Ten parameter models of soil compaction curves used in this study |
本研究采用的土壤样品来自黑龙江省海伦市胜利村(126°79'E,47°43'N)。研究区土壤平均黏粒含量361.9 g/kg,粉粒含量525.8 g/kg,砂粒含量112.3 g/kg,质地类型为粉砂质黏壤土(美国制)。采样时间为2023年5月。为探索轮式农机进地作业导致土壤压实,布置了拖拉机压实次数田间试验(东方红拖拉机LX1304,无负载自重5 030 kg,车速匀速0.56 m/s),设置了拖拉机压实1、3、5、7、9次共5种处理。压实次数试验结束后,在5个压实处理和未压实对照CK处理的0 ~ 5、5 ~ 15、15 ~ 25、25 ~ 40 cm土层均采集60 cm3环刀样,3次重复(重复样本取平均值进行后续结果分析),共24个原状土样本。同时,从未压实处理区采集土样,磨土风干后在实验室内填装60 cm3环刀,设置不同初始容重、含水量以模拟不同土壤条件。初始容重设置4个水平,分别为1.00、1.10、1.20和1.30 g/cm3;含水量设置7个水平,分别为0.15、0.20、0.25、0.30、0.35、0.40和0.50 g/g。含水量和初始容重完全排列组合,3次重复,重复样本取平均值,共28个填装土样本。
1.3 室内单轴压缩试验室内单轴固结压缩试验使用GZQ-1型全自动气压固结仪,按照试验步骤逐级加载压力,压力级别为12.5、25、50、100、200、300、400、600、800、1 000、1 200和1 600 kPa共12级,根据GB/T 50123—2019《土工试验方法标准》[24]计算不同压力状态下的土壤孔隙比、含水量、压缩指数和回弹指数等。
1.4 压实曲线参数模型评价利用Python自行编制了土壤压实曲线模型计算程序,可利用单轴压缩试验获得的荷载压力-土壤孔隙比数据,用非线性最小二乘法优化拟合土壤压实曲线参数模型,获得最优拟合参数,计算土壤压缩指数、回弹指数、预固结压力等压实特征参数。为评价不同模型的拟合效果,采用3种统计指标来进行评价,即赤池信息量准则AIC(Akaike information criterion)、决定系数(R2)、均方根误差(RMSE)。AIC引入拟合参数的数量,对拟合参数过多的模型进行惩罚,可用于评价模型的相对优劣,AIC值越小表明模拟结果越好[25]。
| $ \begin{array}{l}\text{AIC}=\left(-2\right)\mathrm{ln}\left(模型的极大似然函数\right)+\\ 2\left(模型的独立参数个数\right)\end{array} $ | (1) |
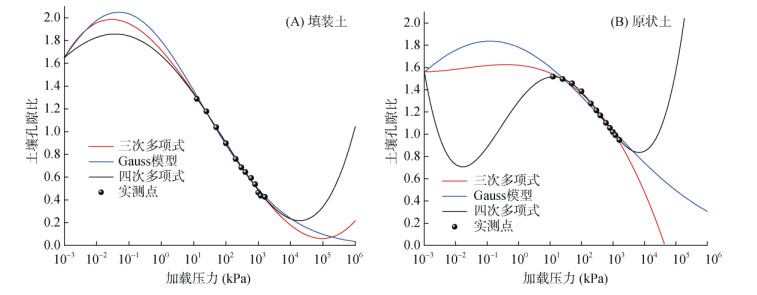
对10个土壤压实曲线参数模型的数值预试验表明,三次多项式、四次多项式、Gauss模型在拟合填装土和原状土实测荷载-孔隙比数据时,虽然拟合效果总体较好(四次多项式在10个模型中表现最好,其AIC、RMSE最小,R2最大),但在压实曲线的起始段(0 ~ 10 kPa)和结尾段(104 ~ 106 kPa)出现过度拟合现象,曲线形态偏离了实测值(图 1),没有实际物理意义,因此在后续结果分析中将这3个模型剔除,仅讨论其他7个模型的计算结果。
|
图 1 填装土和原状土压实曲线3个模型拟合值和实测值的对比 Fig. 1 Comparison of soil compaction curves measured and fitted of disturbed and undisturbed soils |
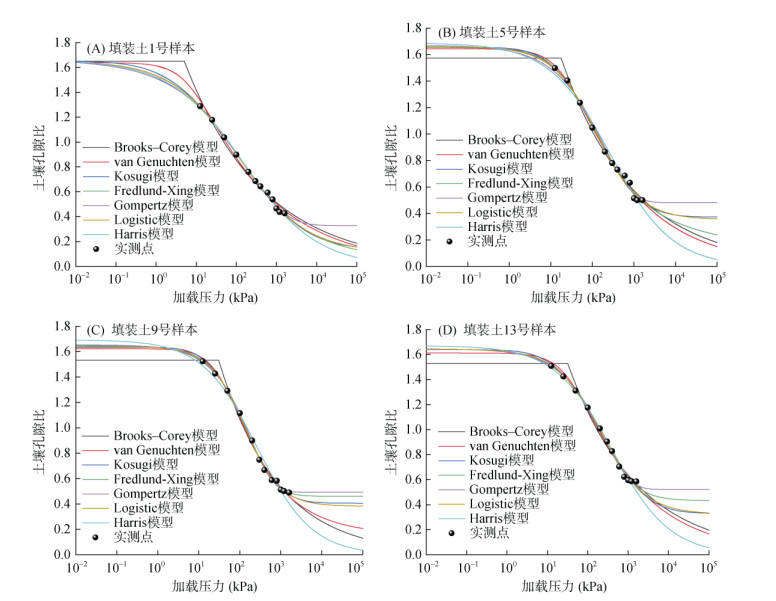
表 2为7个土壤压实曲线参数模型计算的填装土平均AIC、R2和RMSE。从表中可知,7个模型的拟合效果总体上均令人满意,R2 > 0.98,RMSE < 0.012。具体来看,Fredlund-Xing模型的拟合效果最优,其AIC最小(–113.055 7),R2最大(0.998 8),RMSE最低(0.002 8)。随后按照精度由高至低依次为Logistic、Kosugi、Gompertz、van Genuchten、Harris和Brooks-Corey模型。Brooks-Corey模型的效果最差,AIC = –76.646 5,R2 = 0.982 7,RMSE = 0.011 3,明显比其他6种模型差。其原因在于,Brooks–Corey模型为不连续的分段函数,拟合曲线从初始压力到102 kPa时的孔隙比为常数,与实际压实过程不符(图 2)。
|
|
表 2 填装土土样7个土壤压实曲线参数模型的误差统计(n=28) Table 2 Error statistics of seven soil compaction curve parameter models of filled soil samples |
|
图 2 填装土随机4个样本实测和拟合压实曲线对比 Fig. 2 Comparison of soil compaction curves measured and fitted of 4 disturbed samples |
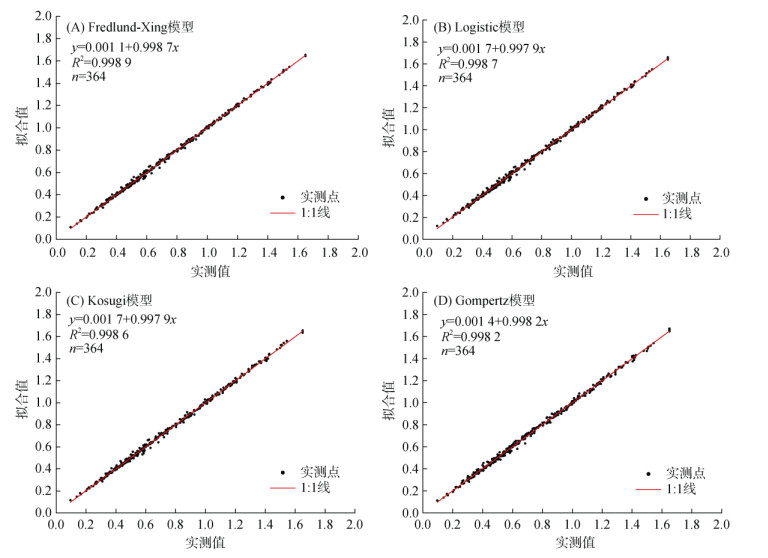
由表 2和图 3可见,Fredlund-Xing、Logistic、Kosugi和Gompertz 4个模型的拟合效果相近,实测和拟合孔隙比间的R2>0.998、RMSE<0.004、AIC<–107,明显优于van Genuchten模型和Harris模型(表 2)。4个模型拟合孔隙比与实测孔隙比接近(图 3)。从曲线形态来看,4个模型的拟合曲线在低荷载压力的弹性形变段(0 ~ 102 kPa)以及压缩曲线接近直线的塑性形变段(102 ~ 103 kPa)基本一致,区别主要体现在高荷载压力段(>103 kPa)。其中,Gompertz模型倾向于较早达到压实曲线的渐近值;Logistic模型与Kosugi对数正态分布模型的拟合曲线几乎重叠;包含5个形状参数的Fredlund-Xing模型则表现出更高的灵活性和拟合精度。
|
图 3 四个最优模型拟合与实测土壤孔隙比的对比(填装土) Fig. 3 Comparison of void ratios measured and fitted by four optimal models (disturbed soils) |
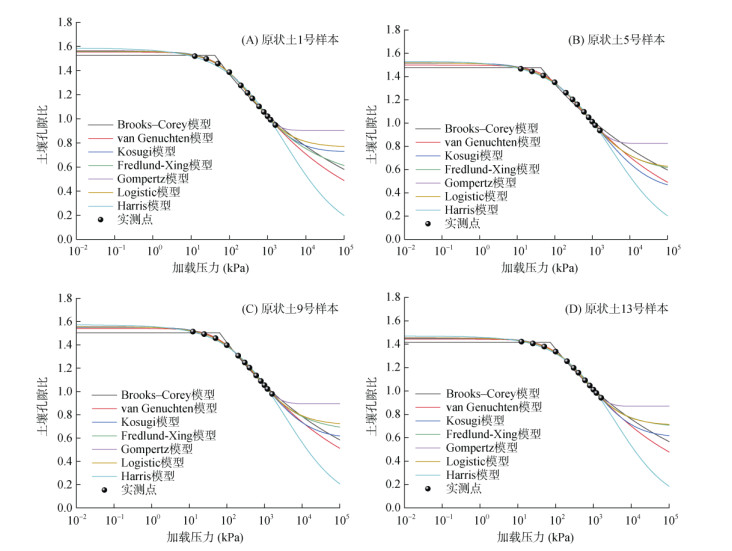
表 3为原状土样本7个土壤压实曲线模型计算的平均AIC、R2和RMSE。可以看出,7个模型的拟合效果总体上均较好(R2 > 0.98,RMSE < 0.007),各模型的相对优劣次序与填装土一致,从优至劣依次为Fredlund-Xing、Logistic、Kosugi、Gompertz、van Genuchten、Harris、Brooks-Corey模型。其中,Fredlund-Xing模型表现最优,AIC = –138.314 1,R2 = 0.999 7,RMSE = 0.001 0。Brooks-Corey模型仍表现不佳,预测效果显著劣于其他6个模型。在其他5个模型中,Logistic模型的拟合精度非常接近Fredlund-Xing模型(AIC= –137.783 3,R2= 0.999 6,RMSE= 0.001 1);Kosugi、Gompertz、van Genuchten 3个模型的评价指标接近(AIC < –126.00,R2 > 0.999 0,RMSE < 0.001 6),略差于Fredlund-Xing模型和Logistic模型;Harris模型仅包含3个形状参数,拟合效果劣于除Brooks-Corey外的其他模型。
|
|
表 3 原状土土样7个土壤压实曲线参数模型的误差统计(n=24) Table 3 Error statistics of seven soil compaction curve parameter models of undisturbed soil samples |
分析Fredlund-Xing、Logistic、Kosugi、Gompertz等拟合效果较好的模型曲线形态(图 4)可知,与填装土结果类似,4个模型的拟合曲线在弹性形变段(0 ~ 102 kPa)、塑性形变段(102 ~ 103 kPa)基本重叠,区别主要在高荷载压力段(> 103 kPa)。4个模型的拟合孔隙比接近实测孔隙比(图 5)。其中,Gompertz模型仍倾向于较早达到压实曲线的渐近值;Fredlund-Xing模型与Logistic模型的拟合结果几乎完全一致,其高压力段(> 103 kPa)的拟合曲线基本位于Gompertz模型和Kosugi模型结果之间。
|
图 4 原状土随机选取的4个样本实测和拟合曲线对比 Fig. 4 Comparison of soil compaction curves measured and fitted of 4 undisturbed samples |
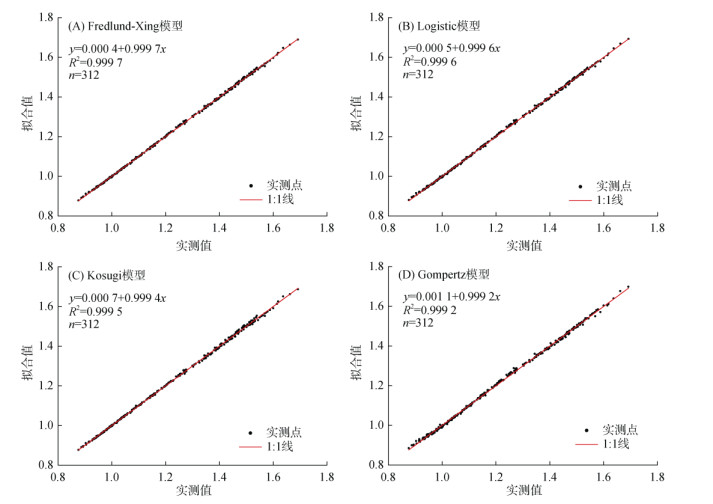
|
图 5 四个最优模型拟合与实测土壤孔隙比的对比(原状土) Fig. 5 Comparison of void ratios measured and fitted by four optimal models (undisturbed soils) |
从填装土和原状土的拟合效果来看,7个模型总体均较好,即使是拟合效果相对较差的Harris模型,其在填装土和原状土上的R2也均大于0.99。但对比表 2和表 3发现,无论是AIC、R2或RMSE,同一模型在原状土上的拟合效果均略优于填装土。如Fredlund-Xing模型在原状土的AIC = –138.314 1、R2 = 0.999 7、RMSE=0.001 0,而在填装土的AIC = –113.055 7、R2 = 0.998 8、RMSE = 0.002 8;Logistic模型在原状土的AIC = –137.783 3、R2 = 0.999 6、RMSE = 0.001 1,而在填装土的AIC = –112.618 1、R2 = 0.998 6、RMSE = 0.003 1。分析其原因,可能是因为填装土是经过人工过筛、研磨和填装,土壤颗粒在田间的自然排列分布状态被扰动,试验中无法反映田间状态下的土壤结构和应力历史;其次,为达到试验目的,人为设置了样品不同的初始容重和含水率,进一步改变了土壤的孔隙结构和水分状态;此外,在室内单轴压缩试验中,随加载压力的增大,填装土的孔隙比变化区间(0.109 7 ~ 1.670 6)远大于经过轮胎碾压的原状土(0.877 9 ~ 1.699 1),填装土的实测压实曲线点间也更加离散(图 2、图 4),这在一定程度上也降低了模型最优化求解时的精度。
本文探讨的7个土壤压实曲线参数模型均为非线性的经验函数,需要利用最优化算法和室内试验数据序列来确定函数中形状参数取值。7个模型中,除Harris模型为3个参数,Fredlund-Xing模型为5个参数外,其余5个模型均包含4个形状参数。一般来说,模型中的参数个数越多,拟合实测值的精度越高,但在最优化求解时需要的实测点数量也会越多,从而会影响模型的实用性。在具体应用中,可根据实测压实曲线数据的多少来选用不同参数个数的模型,实测数据多于5个时,可选择精度最高的Fredlund-Xing模型;实测数据少于或等于4个时,可选择3参数的Harris模型;其他情况下,则可选择Logistic、Kosugi或Gompertz等4参数模型。需要指出的是,Logistic模型的拟合效果仅次于Fredlund-Xing模型,但从严格的数学意义上讲,其曲线前半段和后半段是以曲线拐点为中心对称分布的[13],而实际的土壤压实曲线并不一定是对称分布的,在实际应用中需注意。
4 结论本研究利用黑龙江海伦典型黑土28个填装样品、24个原装样品的室内单轴压缩试验数据,分析评价了10种经验性土壤压实曲线参数模型的拟合效果。Fredlund-Xing、Logistic、Kosugi、Gompertz等4个模型对土壤孔隙比的拟合效果良好,R2均大于0.998,RMSE均小于0.004,适用于填装土和原状土压实曲线的定量描述。其中5参数的Fredlund-Xing模型效果最好,其R2 > 0.998,RMSE < 0.003,推荐在实际研究中使用。而三次多项式、四次多项式、Gauss模型和Brooks-Corey模型拟合结果偏离了实际土壤压实曲线形态,不建议使用。
| [1] |
高晨, 李晓鹏, 刘毅仁, 等. 农田土壤压实过程及模型研究进展[J]. 土壤, 2024, 56(1): 1-9 (  0) 0) |
| [2] |
任利东, 王丽, 林琳, 等. 农田土壤机械压实研究进展与展望[J]. 土壤学报, 2023, 60(3): 610-626 (  0) 0) |
| [3] |
孙奥博, 安晶, 虞娜, 等. 铁矿尾砂配施有机物料对褐土压缩及回弹特性的影响[J]. 土壤, 2022, 54(6): 1300-1306 (  0) 0) |
| [4] |
林琳, 韩少杰, 王恩姮. 有机质与黏粒含量对黑土压缩–回弹特性的影响[J]. 土壤学报, 2016, 53(5): 1138-1147 (  0) 0) |
| [5] |
Zolfaghari Z, Mosaddeghi M R, Ayoubi S. Relationships of soil shrinkage parameters and indices with intrinsic soil properties and environmental variables in calcareous soils[J]. Geoderma, 2016, 277: 23-34 DOI:10.1016/j.geoderma.2016.04.022 (  0) 0) |
| [6] |
Lin L, De Pue J, Vivanco A K M, et al. Visual assessment of soil structural quality across soil textures and compaction levels–part Ⅰ: Examination of intact soil cores[J]. Geoderma, 2022, 426: 116099 DOI:10.1016/j.geoderma.2022.116099 (  0) 0) |
| [7] |
Bayat H, Sheklabadi M, Moradhaseli M, et al. Grazing management, slope aspect and canopy effects on the compression characteristic of soils of the Gonbad experimental watershed in Hamedan, Iran[J]. Geoderma, 2022, 409: 115641 DOI:10.1016/j.geoderma.2021.115641 (  0) 0) |
| [8] |
Saha A, Nath A, Dey A K. Multivariate geophysical index-based prediction of the compression index of fine-grained soil through nonlinear regression[J]. Journal of Applied Geophysics, 2022, 204: 104706 DOI:10.1016/j.jappgeo.2022.104706 (  0) 0) |
| [9] |
Yang P P, Dong W X, Heinen M, et al. Soil compaction prevention, amelioration and alleviation measures are effective in mechanized and smallholder agriculture: A meta-analysis[J]. Land, 2022, 11(5): 645 DOI:10.3390/land11050645 (  0) 0) |
| [10] |
Sánchez-Girón V, Andreu E, Hernanz J L. Response of five types of soil to simulated compaction in the form of confined uniaxial compression tests[J]. Soil and Tillage Research, 1998, 48(1/2): 37-50 (  0) 0) |
| [11] |
Arvidsson J, Keller T. Soil precompression stress Ⅰ. A survey of Swedish arable soils[J]. Soil and Tillage Research, 2004, 77(1): 85-95 (  0) 0) |
| [12] |
Baumgartl T, Köck B. Modeling volume change and mechanical properties with hydraulic models[J]. Soil Science Society of America Journal, 2004, 68(1): 57-65 (  0) 0) |
| [13] |
Gregory A S, Whalley W R, Watts C W, et al. Calculation of the compression index and precompression stress from soil compression test data[J]. Soil and Tillage Research, 2006, 89(1): 45-57 (  0) 0) |
| [14] |
霍连飞, Belal E A, 丁启朔, 等. 采用Gompertz函数的水稻土压缩特性研究[J]. 农业工程学报, 2020, 36(12): 136-142 (  0) 0) |
| [15] |
郎林智, 陈鹏宇, 聂良佐, 等. 基于Gaussian模型的先期固结压力确定[J]. 水电能源科学, 2011, 29(7): 47–49, 194 (  0) 0) |
| [16] |
Brooks R H, Corey A T. Hydraulic properties of porous media[D]. Colorado: Colorado State University, 1965.
(  0) 0) |
| [17] |
Kosugi K. Lognormal distribution model for unsaturated soil hydraulic properties[J]. Water Resources Research, 1996, 32(9): 2697-2703 (  0) 0) |
| [18] |
van Genuchten M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44(5): 892-898 (  0) 0) |
| [19] |
Fredlund D G, Xing A Q. Equations for the soil-water characteristic curve[J]. Canadian Geotechnical Journal, 1994, 31(4): 521-532 (  0) 0) |
| [20] |
Richards L A. Capillary conduction of liquids through porous mediums[J]. 1931, 1(5): 318–333.
(  0) 0) |
| [21] |
张书宪. 用计算机绘图确定先期固结压力的一种方法[J]. 岩土工程界, 2000(8): 45-46 (  0) 0) |
| [22] |
姬宏, 宋新江. e~lg(p/kPa)曲线中曲率半径最小值的数值求法[J]. 水利水电技术, 2001, 32(10): 46-47 (  0) 0) |
| [23] |
王志亮, 郑明新, 李永池. 求前期固结应力的数学模型研究及应用[J]. 岩土力学, 2005, 26(10): 1587-1590 (  0) 0) |
| [24] |
水利部水利水电规划设计总院, 南京水利科学研究院. 土工试验方法标准: GB/T 50123—2019[S]. 北京: 中国计划出版社, 2019.
(  0) 0) |
| [25] |
刘璋温. 赤池信息量准则AIC及其意义[J]. 数学的实践与认识, 1980, 10(3): 64-72 (  0) 0) |
2. Institute of Soil Science, Chinese Academy of Sciences, Nanjing 211135, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China;
4. University of Chinese Academy of Sciences, Nanjing, Nanjing 211135, China
 2025, Vol. 57
2025, Vol. 57


