2. 中国水利水电科学研究院流域水循环模拟与调控国家重点实验室, 北京 100038
多年冻土活动层作为连接冰冻圈、大气圈、生物圈、水圈和岩石圈的重要纽带[1],其水热传输过程对能水平衡的影响成为活动层监测和研究的重要方向。活动层作为多年冻土与大气进行能水交换的媒介,冻融过程涉及水分迁移、热量传输以及水分相变[2]。冻融过程的水分迁移由于冻土的弱透水性会影响地表径流的形成以及地下水的运移过程[3],同时也会提高融雪和降雨径流的产流量[4],从而直接影响水循环及水量平衡各分项占比。土壤的热量传输在冻融作用下改变了其热力学性质与水分相变,导致土壤冻融过程中释放和吸收相变潜热,从而改变地表能量分配[5]。活动层的水热情况与地气间能水交换变化,不仅会影响冻融循环过程,而且对寒区地表能量平衡、水文过程产生直接影响[6]。明确系统间的能水交换特征,对于认识区域水循环和气候变化的响应有重要意义。
由于冻土地区土壤水冻结无法直接观测冷季土壤固态含水量和涡度相关系统对能量不闭合现象[7]观测的限制,加之多年冻土的冻融复杂过程[8],使得水热传输过程十分复杂,加剧了高海拔地区水能平衡研究的难度。而随着模拟仿真技术的不断发展,模型参数的不断改进,量化水能变化过程的重心也逐渐从数理统计分析向模型转移[9]。SHAW(The simultaneous heat and water)模型考虑了土壤冻融情况下水热耦合的过程和水的相变,被广泛应用于高原冻土区水热变化过程探究[10-12],成为研究冻土区水能平衡过程的重要手段。以往对于长江源唐古拉地区的模拟集中于通过输入不同地表反照率[12]、改变植被叶面积指数[13-4]对土壤温湿度的影响,而对于定量评估能水平衡各分量的研究却少有见闻。为了明确长江源区水热变化规律以及水能平衡特征,本研究基于长江源唐古拉站2020—2021年土壤温、湿度和气象数据,利用SHAW模型对土壤温湿度观测数据进行模拟验证,基于输出结果分析土壤水量平衡和能量平衡变化规律,以期为相关研究提供数据参考及对比,同时为长江源冻土区能水平衡提供理论依据和数据支持。
1 材料与方法 1.1 研究区域与数据来源本文基于水利部长江源区水生态系统野外科学观测研究站和中国科学院西北研究院唐古拉冰冻圈与环境观测研究站(TGL,33°0′N,91°41′E)获取了各项数据。该站位于长江源区的多年冻土区,海拔5 100 m,土壤质地以砂土为主[14],植被群落类型主要为高寒草甸,根系深度较浅,植被覆盖度在30% ~ 40% 左右[12]。该地区冷热分明,寒冷季节主要受西风环流影响,温暖季受影响于印度西南部暖湿气流[15]。研究区年平均气温在–6 ℃左右,极端最低气温–30 ℃,最高温度20 ℃,年平均相对湿度为51%,年降水量约为450 mm,80% 集中在植被生长季[14]。气象站记录数据有气温、降水、风速、湿度、太阳辐射,关于活动层分别在0 ~ 100 cm每间隔10 cm处埋置土壤温度和土壤水分探头,监测土壤温度和液态水分含量变化,监测频率为10 min/次。所用观测仪器及观测项目如表 1所示。
|
|
表 1 观测仪器及相关信息 Table 1 Observation instruments and related information |
SHAW模型是为了模拟土壤冻融而开发的[16],该模型能够模拟植被、雪、残留物覆盖下的一维剖面上的土壤水热运动,可用于评估气候对水文过程的影响。因其将系统内物质与能量交换的各物理过程集成到同步解决方案,所以能够准确地模拟土壤温度和水分的动态变化、各土层之间的水分迁移、蒸散发以及地表辐射平衡[17]。
模型模拟具有冻融特性的土壤水通量方程为:
| $ \frac{{\partial {\theta _{\text{l}}}}}{{\partial t}} + \frac{{{\rho _{\text{i}}}}}{{{\rho _{\text{l}}}}}\frac{{\partial {\theta _{\text{i}}}}}{{\partial t}} = \frac{\partial }{{\partial z}}[K(\frac{{\partial \psi }}{{\partial z}} + 1)] + \frac{1}{{{\rho _{\text{l}}}}}\frac{{\partial {q_{\text{v}}}}}{{\partial z}} + U $ | (1) |
式中:
计算土壤热量传输时,模型考虑冻土中液体对流传热和蒸气潜热,土壤基质中温度分布的状态方程:
| $ \begin{array}{l} {C_{\text{s}}}\frac{{\partial T}}{{\partial t}} - {\rho _{\text{i}}}{L_{\text{f}}}\frac{{\partial {\theta _{\text{i}}}}}{{\partial t}} = \frac{\partial }{{\partial z}}[{K_{\text{s}}}\frac{{\partial T}}{{\partial z}}] - {\rho _{\text{l}}}{c_{\text{l}}}\frac{{\partial {q_{\text{l}}}T}}{{\partial z}} - \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{L_{\text{v}}}(\frac{{\partial {q_{\text{v}}}}}{{\partial z}} + \frac{{\partial {\rho _{\text{v}}}}}{{\partial t}}) \hfill \\ \end{array}$ | (2) |
式中:
模型的输入主要依靠气象驱动数据、模拟站点的位置数据以及模拟开始和结束时间段的土壤温湿度数据,其中气象驱动数据包括小时气象数据和日气象数据,本研究选取日气象数据,具体包括日最高/低温度(℃)、露点温度(℃)、风速(m/s)、降雨量(mm)以及太阳辐射(W/m2)。模拟站点的位置信息包括唐古拉站点的经纬度、坡度、坡向、海拔等,以及土壤特征参数、水力特征参数和土壤各剖面的温湿度。本文模拟了2020年1月1日至2021年12月31日活动层0 ~ 100 cm土壤剖面的温湿度,通过对比实测与模拟之间差异,来验证模型的有效性。基于输出的结果,分析讨论土壤水量平衡和地表能量平衡。将土壤剖面分为0、10、20、30、40、50、60、70、80、90、100 cm共11层,土壤水分温度数据来源于实测数据,模型的下边界条件为100 cm土层处土壤温湿度,上边界条件为日尺度的气象资料(图 1),各层土壤的颗粒组成、容重参考文献[13](表 2),干燥土壤与湿润土壤的地表反照率分别取0.30和0.35,土壤水分特征曲线模型选取Campbell模型,饱和导水率、饱和体积含水率、空气进入势以及坎贝尔分布指数参照前人的率定成果[16,18],以温湿度的模拟最优为目标采用手动率定。积雪参数方面,积雪动量传递的风廓线粗糙度参数取0.15,其余参数均取模型的建议值。
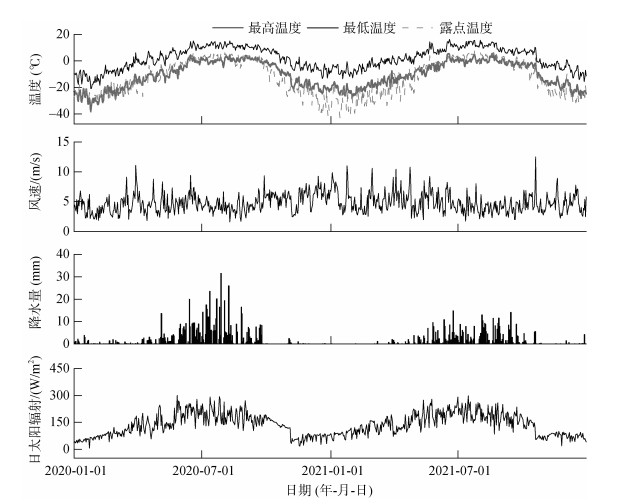
|
图 1 试验区气象数据 Fig. 1 Meteorological data of test area |
|
|
表 2 SHAW模型各层土壤特征参数 Table 2 Soil characteristic parameters of each layer of SHAW model |
模型通过统计学相关参数进行评价,本文选取纳什效率系数(NSE)、均方根误差(RMSE)、拟合优度(R2)、平均绝对误差(MAE)等参数对模型进行可行性评价。具体计算公式如下:
| $ {\text{NSE}} = 1 - \frac{{\sum\limits_{n = 1}^N {{{(Q_{\text{o}}^n - Q_{\text{m}}^n)}^2}} }}{{\sum\limits_{n = 1}^N {{{(Q_{\text{o}}^n - \overline {Q_{\text{o}}^n} )}^2}} }} $ | (3) |
| $ {\text{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{n = 1}^N {{{(Q_{\text{o}}^n - Q_{\text{m}}^n)}^2}} } $ | (4) |
| $ {R^2} = 1 - \frac{{\sum\limits_{n = 1}^N {{{(Q_{\text{m}}^n - Q_{\text{o}}^n)}^2}} }}{{\sum\limits_{n = 1}^T {{{(\overline {Q_{\text{o}}^n} - Q_{\text{o}}^n)}^2}} }} $ | (5) |
| $ {\text{MAE}} = \frac{1}{N}\sum\limits_{n = 1}^N {\left| {Q_{\text{o}}^n - Q_{\text{m}}^n} \right|} $ | (6) |
式中:N表示观测样本总数;
为评估研究区土壤水分占比与变化过程,本研究基于土壤水量平衡法计算各分量占比,具体计算公式:
| $ P = {\text{ET}} + \Delta W + D + R - I - K $ | (7) |
式中:P表示降水量(mm);ET为蒸散发(mm);
根据热力学第一定律,地表能量平衡方程可表示为:
| $ H + {\text{LE}} = {R_{\text{n}}} - {G_{\text{o}}} - S - Q $ | (8) |
式中:H表示感热通量(W/m2);LE表示潜热通量(W/m2);Rn表示净辐射通量(W/m2);Go表示土壤热通(W/m2);S、Q分别表示冠层热储量与附加能量源汇的综合,因其数值较小通常不予考虑。
2 结果与讨论 2.1 土壤温度模拟SHAW模型在代表性土层深度处土壤温度实测值与模拟值的变化特征见图 2,土壤温度模拟效率参数如表 3所示。所有土层深度土壤温度模拟值与观测值的NSE > 0.93,RMSE < 2 ℃,R2 > 0.97,MAE < 1.6 ℃,表明模型在土壤温度模拟中具有良好的可靠性。10 cm处的NSE、RMSE、R2、MAE分别为0.94、1.84 ℃、0.99、1.55 ℃,而90 cm处的NSE、RMSE、R2、MAE分别为0.98、0.50 ℃、1.00、0.43 ℃,随着土层深度的增加模型的模拟精度不断提高。这是因为以100 cm土层作为下边界约束,表层土壤温度受大气温度与太阳辐射影响程度较高且不同土层土壤温度传递与能量传输密切相关,因此,土层越接近下界面时,土壤温度模拟结果与实测值更匹配,这一结果与风火山地区[13]、青海湖流域[19]、北疆地区[20]土壤温度模拟结果一致。而70 cm土层模拟效果却劣于相邻上土层,可能是由于观测点土壤参数的不确定性,从而引起模拟效果的偏差。Flerchinger和Hardegree[21]对土壤温度优化模拟的研究中发现,若输入的土壤质地、容重等土壤热特性参数在合理范围内,绝大多数参数对土壤温度的输出都不敏感。土壤温度模拟随时间的变化表现为暖季(5—10月)模拟效果优于冷季(11—4月)。暖季土壤温度的模拟值低于实测值;冷季0 ~ 60 cm模拟值低于实测值,60 ~ 100 cm模拟值高于实测值。可能是SHAW模型将土壤的导热系数、热容假设为土壤内液态水、冰、土壤颗粒的加权值,在冷季干燥和暖季湿润的条件下导致热传导过程[22]的计算偏差导致土壤温度模拟偏差[17]。
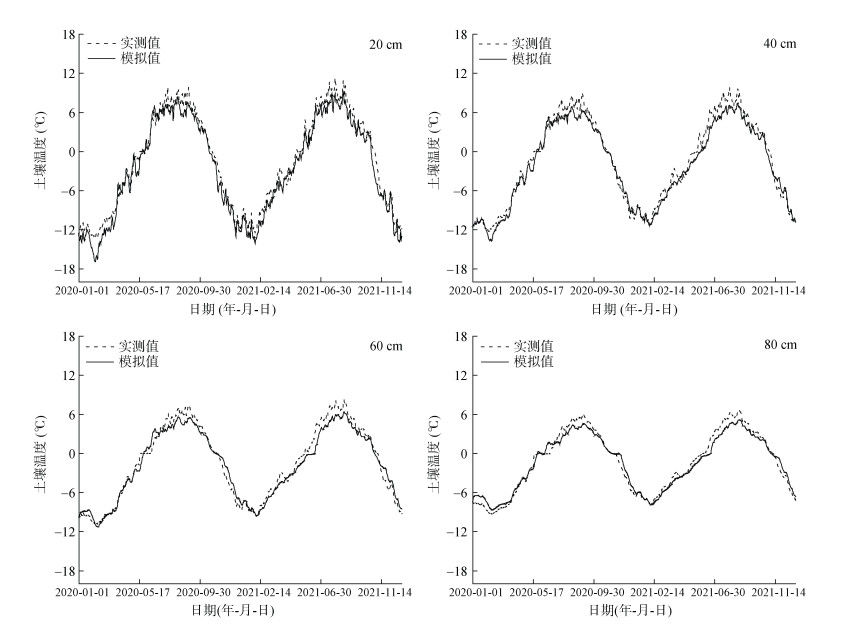
|
图 2 2020—2021年代表性土层深度观测和模拟土壤温度对比 Fig. 2 Comparison of observed and simulated soil temperatures at representative depths from 2020 to 2021 |
|
|
表 3 SHAW模型土壤温度模拟效率参数 Table 3 Efficiency parameters of soil temperature simulation in SHAW model |
土壤湿度模拟值与实测值的变化特征见图 3,模拟特征参数见表 4。从模拟效果来看,NSE均值> 0.61,R2均值> 0.79,基本能反映土壤湿度的变化趋势。随着土层深度加深,土壤湿度的模拟并未表现出如土壤温度随深度增加不断上升的趋势,这是因为土壤湿度存在0 ℃冰点,当土壤温度达到0 ℃,土壤水发生相变,而冰的热容相较于水更低,故影响水分的模拟效果。表层、中层土壤水分NSE均值达到0.69,而70 cm、80 cm深度NSE仅为0.31和0.47。对于深层土壤湿度模拟效率较差,是由于土层间热传导的相关性很大程度上受土壤特性以及垂向和横向水流的影响,相较于土壤温度更复杂。研究区降水有限,导致深层土壤先达到饱和状态更容易发生侧向流,SHAW模型为一维剖面模型,没有考虑侧向流。从不同季节上来看,土壤水分波动较大的时间节点仅在冷暖季交替、土壤水分发生冻融期间,这与郭东林和杨梅学[23]在那曲站的研究结果一致。暖季土壤水分波动较大,冷季土壤水分变化较为平稳,降水成为影响其变化的主要因素[24]。另外在冷季水分模拟值高于实测值,可能是实测仪器的测量偏差导致。冷暖交际期间,各土层土壤湿度实测值突变点均在同一天内,而模拟值突变点均有不同程度的滞后,这与土壤温度模拟值的正负直接相关,SHAW模型根据温度区分液态水与固态水。
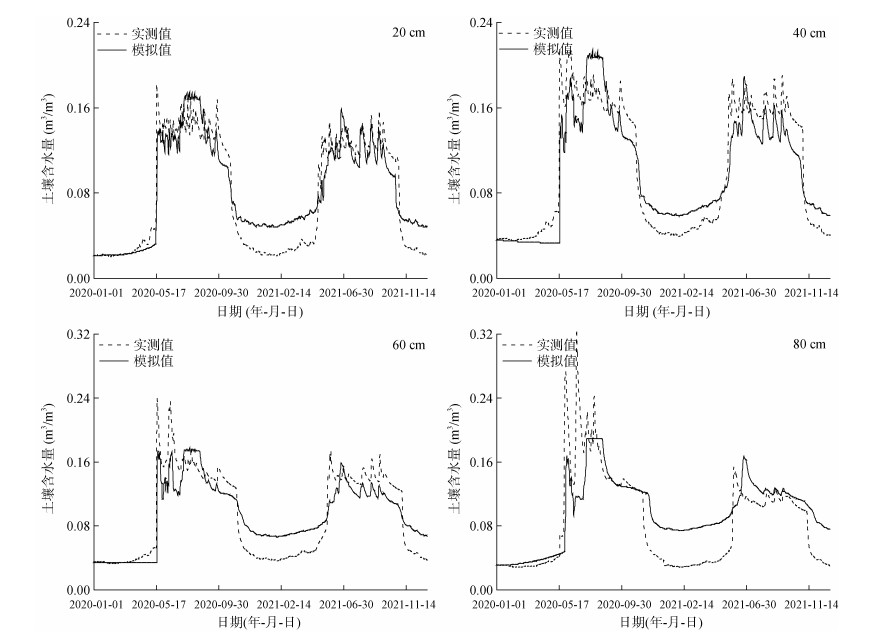
|
图 3 2020—2021年代表性土层深度观测和模拟土壤含水量对比 Fig. 3 Comparison of observed and simulated soil moistures at representative depths from 2020 to 2021 |
|
|
表 4 SHAW模型土壤含水量模拟效率参数 Table 4 Efficiency parameters of soil moisture simulation in SHAW model |
唐古拉站点模拟土壤含水量随土层深度变化的时间剖面见图 4,可以看出在2020年暖季土壤含水量明显高于2021年,且随着土层深度的增加土壤含水量逐渐上升,分别在50 cm和90 cm处达到极大值。2020—2021年土壤含水量维持在0.02 ~ 0.41 m3/m3,在冷季土壤冻结含水量在0.1 m3/m3以下,暖季土壤融化含水量上升至0.2 ~ 0.4 m3/m3。模拟值相比于实测值在融化期和冻结期会有不同时间的延后与提前,但基本趋势保持一致。
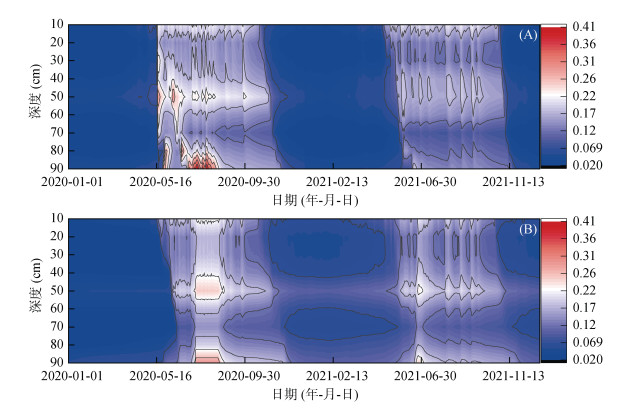
|
(A.观测值;B.模拟值) 图 4 土壤含水量(m3/m3)随土层深度变化的时间剖面 Fig. 4 Time profiles of observed and simulated soil moistures with depth |
深层渗漏是指降水或灌溉量过大,土壤水分向植被根系活动层以下的土层产生渗漏,从而补给地下水或含水系统的过程。本模拟中,设定100 cm为模型的下边界,将水分通量向下视为深层渗漏,向上视为补给。
下边界处2020—2021年土壤深层渗漏与补给的变化过程模拟如图 5所示,100 cm土体与下土层暖季交换频繁。降水量变化过程基本表现为暖季(5—10月)降水丰富,冷季(11—4月)基本无降水。2020年暖季累积降水量为619.43 mm,占全年的92%;2021年暖季降水量为430.88 mm,占全年94.6%;降水量年际间减少,但暖季降水占比增加。关于渗漏量,经分析,深层渗漏主要发生在降水之后,渗漏量与降水量之间表现出正相关关系。2020年渗漏主要发生在6月20日至10月2日,渗漏系数可达0.60,即60% 的降水量渗漏到100 cm土层以下,渗漏量为278.66 mm。冷季渗漏量较少,主要是因为降水量较小,土壤水分无法补给到底层,而模型下边界为100 cm,不同量级的降水量对土壤水分的补给深度也有重要影响[25],同时该时期土壤温度较低,土壤水处于冻结状态。2021年渗漏期基本与2020年保持一致,此间渗漏系数为0.41,渗漏系数在年际间表现出较大的不确定性。土壤水补给量无明显的季节变化规律,主要发生在6—8月以及10—12月,6—8月由于大量降水引起渗漏,造成下边界层上下水势差从而出现深层向上补给,而在10—12月因土壤冻结作用造成边界上下处含水率的差异,但此间无降水故深层向上补给量较小。2020年深层土壤水补给量为106.95 mm,2021年为47.01 mm,占水分总输入的12%。值得一提的是2020年7月16日补给量达到29.29 mm,根据降水量分布可知2020年为丰水年,且7月8—13日期间4次中雨(10 ~ 24.9 mm)使得水分通过砂质土壤快速入渗至下边界以下,使得深层土壤水的水势高于下边界层,尽管短时期内的降水无法使土壤达到饱和状态,但仍有水分通过[26],而深层水分通过毛管作用力来补给相邻土层。
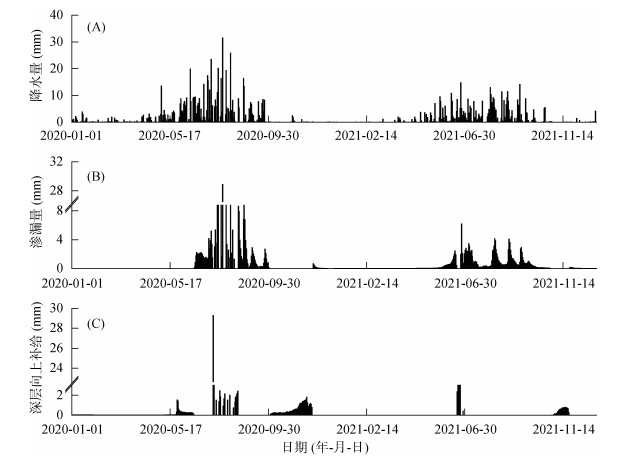
|
图 5 土壤水量平衡分项:降水量(A)、渗漏量(B)、深层向上补给量(C) Fig. 5 Components of water balance: precipitation (A), seepage (B), deep upward recharge (C) |
下边界以上2020—2021年水量平衡分项中蒸散发(由于模型未输入植被项,蒸散发仅包括土壤蒸发)和土壤储水量的变化过程(地表积水变化量极小忽略不计)见图 6。土壤蒸发作为水分输出的主要项,主要集中在暖季,冷季几乎为零(图 6A)。2020年土壤蒸发的最大速率为4.97 mm/d,年土壤蒸发量为383.55 mm,暖季土壤蒸发量为332.48 mm,占年蒸发量的86.7%;2021年土壤蒸发的最大速率为4.86 mm/d,年蒸发量为376.43 mm,暖季土壤蒸发量为348.29 mm,占全年累积蒸发量的94.3%。年际间土壤蒸发量基本无明显变化,该结果与余文君等[27]在青藏高原研究区多年平均蒸散发371.54 mm基本一致。由于植被文件缺少,限制了植被蒸腾占蒸散发比重的计算与实际蒸散发量的模拟情况。
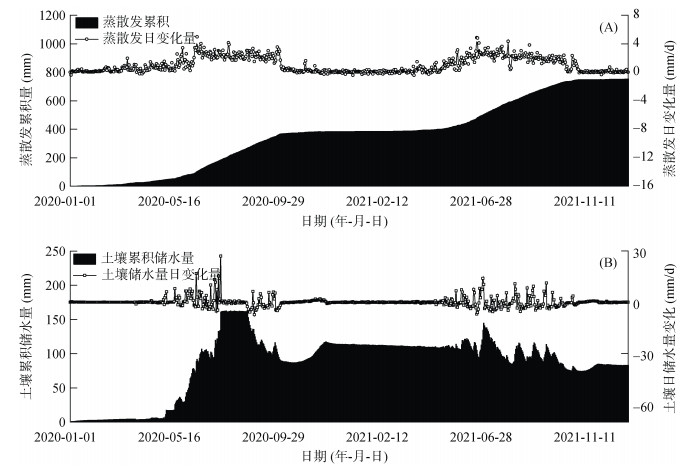
|
图 6 土壤水量平衡分项:蒸散发(A)、土壤储水量(B) Fig. 6 Components of water balance: evapotranspiration (A), soil water storage (B) |
土壤储水量变化见图 6B,与土壤蒸发具有相同的趋势,暖季土壤水分波动剧烈,冷季变化平稳。土壤储水量日变化在暖季为0.13 mm/d,冷季为0.10 mm/d。2020年5月初至7月中旬土壤累积储水量急剧上升,至162 mm;从7月中旬到8月中旬土壤水分保持稳定,直至10月储水量不断下降。2021年土壤储水量波动频繁,在6月末储水量达到峰值,随后出现波动。两年间土壤累积储水量达到83.15 mm,2021年总体表现为支出,可能由于降水量相较于2020年较小,土壤储水量与降水量直接相关[28]。
2.3.3 土壤水量平衡特征土壤水量平衡各分项占比与具体值见图 7与表 5。降水是土壤水分的主要来源,该研究期内降水量占来水量的86.4%,年平均降水为564.06 mm,深层向上补给量为76.98 mm。蒸散发是土壤水分支出的主要消耗源,但本次模拟缺少植被的蒸腾量模拟,可能会成为影响模拟效果的主要因素。蒸散发占水分支出的49.1%,年均值可达376.43 mm;其次是渗漏占比36% 具体为221.01 mm;土壤储水量与地表积水分别占14.4% 和0.5%,分别为41.57和2.03 mm。
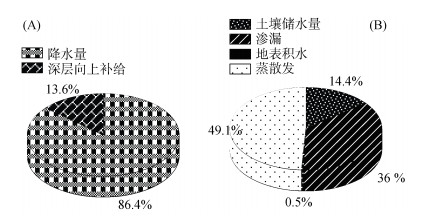
|
图 7 土壤水量平衡收入项(A)和支出项(B) Fig. 7 Soil water balance income (A) and expenditure (B) |
|
|
表 5 土壤水量平衡参数年均值 Table 5 Annual average values of water balance parameters |
地表能量收支具有明显的冷暖季交替的变化特征(图 8)。在暖季,从5月开始感热通量不断减小,潜热通量不断上升,在6—9月份保持在较高水平,净辐射通量主要转化为潜热通量,并且此时土壤热通量也达到峰值,但在10月份迅速降低为负值。由图 2实测土壤含水量可知土壤冻结开始于10月,活动层内部释放热量,同时潜热通量迅速减小,感热通量增大,二者在10月初达到相等。相关研究表明亚洲季风[29]与土壤冻融[30]成为影响青藏高原能量平衡的关键因素。亚洲季风通常始于暖季,季风活动引起降水量加剧与降水频率提升,使得土壤湿度提高,同时蒸散发加剧造起潜热通量远大于显热通量。在冷季,感热通量持续大于潜热通量,二者于5月份达到相等水平。该时期内,净辐射通量绝大部分转化为感热通量,因为该阶段土壤液态水含量较低,土壤水大多处于冻结状态。土壤热通量直至3月份由负值逐渐变为正值,活动层内部开始吸热。根据图 2可知土壤冻融迅速变化发生在10月与5月,该时期感热通量与潜热通量变化剧烈。潜热通量在10月份随着活动层冻结,冻结锋面以上水分的相变以及热传导迅速减小,感热通量在暖冷交际处呈增大趋势。一方面活动层冻结释放能量用于地表加热的能量增多,驱动感热通量的大气与地表之间的温度梯度增大,感热通量呈增大趋势;另一方面冷季降水量减少,土壤含水率较低,净辐射较少地被显热消耗[14]。在5月由于融化过程中水分的下渗被融化锋面阻挡,使得水分更多用于蒸发,造成潜热显著增加,感热通量则因活动层融化与降水增多表现出与10月相反的趋势[17]。
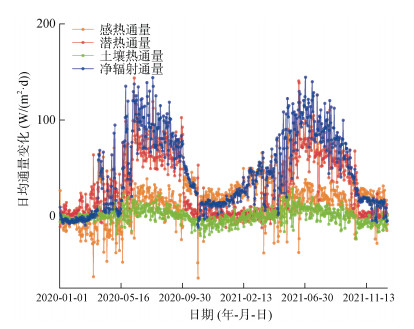
|
图 8 地表能量各分量变化过程 Fig. 8 Change process of each component of surface energy |
能量平衡各参数累积量见表 6,模拟期内净辐射通量年平均值为1 463.65 MJ/m2,日均辐射通量为46.48 W/m2,其中65.1% 转化为潜热通量,可达948.31 MJ/m2,暖季潜热通量达全年潜热通量的89.6%;32.7% 转化为显热通量,冷季显热通量占全年显热通量的42.8%;土壤热通量仅占0.3%,且向大气释放能量。
|
|
表 6 能量平衡参数年均值 Table 6 Annual average values of energy balance parameters |
1) SHAW模型对研究区土壤温度的模拟效果较好,NSE > 0.93,R2 > 0.97,模拟效果随土层深度增加呈上升趋势;土壤水分的模拟效果不及土壤温度,中层模拟效果较差,但基本能够反映土壤水分动态变化特征。
2) 研究期内,土壤水量平衡各分项具有明显的季节变化特征。降水量暖季丰富、冷季基本为零,深层渗漏经常伴随降水发生,深层水分补给冷暖季均有发生,蒸散发主要集中在暖季,土壤储水量暖季变化剧烈、冷季平稳。降水是土壤水分收入的主要部分,深层渗漏与蒸散发构成土壤水分支出的主体。
3) 地表能量平衡冷暖季交替变化。净辐射通量、潜热通量与土壤热通量暖季先增大后减小,7月达到峰值,冷季呈现先减小后增大;感热通量表现出相反的趋势。季风与冻融作用成为影响净辐射收支的关键因素。模拟期内日均净辐射量65.1% 转化为潜热通量,32.7% 转化为显热通量,土壤热通量仅占0.3%。
| [1] |
Zou D F, Zhao L, Sheng Y, et al. A new map of permafrost distribution on the Tibetan Plateau[J]. The Cryosphere, 2017, 11(6): 2527-2542 DOI:10.5194/tc-11-2527-2017 (  0) 0) |
| [2] |
孙文军. 青藏高原多年冻土不同植被覆盖类型下土壤水热过程特征分析[D]. 兰州: 兰州大学, 2022.
(  0) 0) |
| [3] |
赵林, 胡国杰, 邹德富, 等. 青藏高原多年冻土变化对水文过程的影响[J]. 中国科学院院刊, 2019, 34(11): 1233-1246 (  0) 0) |
| [4] |
Kurylyk B L, MacQuarrie K T B, McKenzie J M. Climate change impacts on groundwater and soil temperatures in cold and temperate regions: Implications, mathematical theory, and emerging simulation tools[J]. Earth-Science Reviews, 2014, 138: 313-334 DOI:10.1016/j.earscirev.2014.06.006 (  0) 0) |
| [5] |
Wang J Y, Luo S Q, Lv Z B, et al. Improving ground heat flux estimation: Considering the effect of freeze/thaw process on the seasonally frozen ground[J]. Journal of Geophysical Research: Atmospheres, 2021, 126(24): e2021JD035445 DOI:10.1029/2021JD035445 (  0) 0) |
| [6] |
Hu G J, Zhao L, Li R, et al. Simulation of land surface heat fluxes in permafrost regions on the Qinghai-Tibetan Plateau using CMIP5 models[J]. Atmospheric Research, 2019, 220: 155-168 DOI:10.1016/j.atmosres.2019.01.006 (  0) 0) |
| [7] |
连海东. 干旱区农田生态系统水热碳通量演化特性及耦合模拟研究[D]. 银川: 宁夏大学, 2023.
(  0) 0) |
| [8] |
嵇海龙. 青藏高原冻土水热过程区域模拟的预热策略影响研究[D]. 南京: 南京师范大学, 2021.
(  0) 0) |
| [9] |
马俊杰, 李韧, 刘宏超, 等. 青藏高原多年冻土区活动层水热特性研究进展[J]. 冰川冻土, 2020, 42(1): 195-204 (  0) 0) |
| [10] |
李乃玉, 吴丽丽, 杨林山, 等. 基于SHAW模型的祁连山浅山区荒漠草地土壤水热动态模拟研究[J]. 冰川冻土, 2024, 46(3): 93-1005 (  0) 0) |
| [11] |
郑丽萍, 甘永德, 魏加华, 等. 基于SHAW模型高寒区冻融土壤水热耦合过程数值模拟[J]. 水利水电技术(中英文), 2022, 53(6): 194-204 (  0) 0) |
| [12] |
刘杨, 赵林, 李韧. 基于SHAW模型的青藏高原唐古拉地区活动层土壤水热特征模拟[J]. 冰川冻土, 2013, 35(2): 280-290 (  0) 0) |
| [13] |
郭林茂, 常娟, 周剑, 等. 唐古拉地区活动层水热状况及地气系统能水平衡分析[J]. 高原气象, 2020, 39(2): 230-233 (  0) 0) |
| [14] |
Yang H, Hong X F, Yuan Z, et al. Modelling the influence of vegetation on the hydrothermal processes of frozen soil in the Qinghai–Tibet plateau[J]. Water, 2023, 15(9): 1692 DOI:10.3390/w15091692 (  0) 0) |
| [15] |
姚檀栋, 张寅生, 蒲健辰, 等. 青藏高原唐古拉山口冰川、水文和气候学观测20 a: 意义与贡献[J]. 冰川冻土, 2010, 32(6): 1152-1161 (  0) 0) |
| [16] |
Flerchinger G N, Saxton K E. Simultaneous heat and water model of a freezing snow-residue-soil system Ⅰ. Theory and development[J]. Transactions of the ASAE, 1989, 32(2): 565-571 DOI:10.13031/2013.31040 (  0) 0) |
| [17] |
郭林茂. 青藏高原风火山地区活动层水热状况及冻结层上水动态变化模拟[D]. 兰州: 兰州大学, 2020.
(  0) 0) |
| [18] |
赵林, 李韧, 丁永建. 唐古拉地区活动层土壤水热特征的模拟研究[J]. 冰川冻土, 2008, 30(6): 930-937 (  0) 0) |
| [19] |
谢婷, 马育军, 杨晨. 基于SHAW模型的青海湖流域土壤温度模拟[J]. 土壤, 2022, 54(1): 161-168 (  0) 0) |
| [20] |
赵露, 叶含春, 王振华, 等. 基于SHAW模型的北疆地区不同滴灌年限棉田冻融期土壤水热盐动态模拟研究[J]. 土壤, 2024, 56(3): 623-638 (  0) 0) |
| [21] |
Flerchinger G N, Hardegree S P. Modelling near-surface soil temperature and moisture for germination response predictions of post-wildfire seedbeds[J]. Journal of Arid Environments, 2004, 59(2): 369-385 DOI:10.1016/j.jaridenv.2004.01.016 (  0) 0) |
| [22] |
张建彬, 高志球, 童兵, 等. 土壤温度预报方程研究进展[J]. 土壤学报, 2023, 60(3): 599-609 (  0) 0) |
| [23] |
郭东林, 杨梅学. SHAW模式对青藏高原中部季节冻土区土壤温、湿度的模拟[J]. 高原气象, 2010, 29(6): 1369-1377 (  0) 0) |
| [24] |
Zhu X F, Wu T H, Zhao L, et al. Exploring the contribution of precipitation to water within the active layer during the thawing period in the permafrost regions of central Qinghai-Tibet Plateau by stable isotopic tracing[J]. Science of the Total Environment, 2019, 661: 630-644 DOI:10.1016/j.scitotenv.2019.01.064 (  0) 0) |
| [25] |
付稳东. 榆林沙地不同覆被类型土壤水分对降水的响应及水量平衡分析[D]. 西安: 长安大学, 2023.
(  0) 0) |
| [26] |
盖佳敏, 樊军, 王胜. 黄土高原粗质地土壤剖面水分运动与浅层地下水补给可能性模拟[J]. 中国生态农业学报, 2018, 26(2): 253-262 (  0) 0) |
| [27] |
余文君, 赵林, 李艳忠, 等. 基于互补相关理论的青藏高原蒸散发时空变化及其影响因素[J]. 生态学报, 2024, 44(12): 5024-5039 (  0) 0) |
| [28] |
周景春, 苏玉杰, 张怀念, 等. 0~50 cm土壤含水量与降水和蒸发的关系分析[J]. 中国土壤与肥料, 2007(6): 23-27 (  0) 0) |
| [29] |
Wu G X, Duan A M, Liu Y M, et al. Tibetan Plateau climate dynamics: Recent research progress and outlook[J]. National Science Review, 2015, 2(1): 100-116 (  0) 0) |
| [30] |
郑汇璇, 胡泽勇, 孙根厚, 等. 那曲高寒草地总体输送系数及地面热源特征[J]. 高原气象, 2019, 38(3): 497-506 (  0) 0) |
2. State Key Laboratory of Simulation and Regulation of Water Cycles in River Basin, China Institute of Water Resources and Hydropower Research, Beijing 100038, China
 2025, Vol. 57
2025, Vol. 57


