2. 河南水利与环境职业学院, 郑州 450008;
3. 河南省地质研究院, 郑州 450001
镉是Ⅰ类致癌物,可以通过食物链进入人体,引发肝脏肾脏疾病[1-2]。2014年发布的《全国土壤污染状况调查公报》[3]显示,重金属镉的点位超标率高达7%,是我国土壤的首要无机污染物。工业“三废”排放和农用化学品大量使用是造成土壤镉污染的主要原因[4]。黄河流域工、农业城市众多,研究黄河流域土壤镉污染的空间分布状况对确定流域生态安全状况、实现黄河流域高质量发展具有重要意义。
土壤重金属的分布受到人为因素[5]、环境因子[6]及土壤理化性质[7-9]等的影响。引入相关影响因素作为辅助变量的预测模型,在不同程度上考虑了影响因素对预测变量空间分布的影响,其预测精度较基于样点数据进行空间内插的方法有明显的提高[10]。Li等[11]以土壤轮作制度、道路交通等人为因素作为预测模型的辅助变量,预测成都地区的土壤镉分布,结果表明,人为因素的引入提高了预测模型的预测精度。江叶枫和郭熙[12]基于地形数据、植被指数等环境因子预测稻田土壤砷分布,结果表明,环境因子的引入提高了预测模型的预测精度。但人为因素作为预测模型的辅助变量难以定量表示,环境因子中的地形因素难以刻画地形平坦区域土壤重金属的空间分布,而土壤理化性质能够克服上述缺点,是土壤重金属空间分布预测模型的理想辅助变量。周伟等[13]利用地理探测器探究土壤重金属空间分布的影响因子,提出土壤理化性质可作为土壤重金属空间预测模型的辅助变量。但前人预测土壤重金属的空间分布多以环境因子、人为因素作为辅助变量,考虑土壤理化性质的研究较少。
在引入辅助变量的预测方法中,回归克里格法[14-15]、多元回归模型[16-17]以及径向基函数(RBF)神经网络模型[18-19]等被广泛应用于预测土壤重金属等的空间分布。土壤重金属的含量与其空间位置之间往往存在着高度复杂的非线性映射关系[20],回归克里格法是基于线性无偏最优估值理论的克里格方法的拓展,在插值时会产生平滑效应;多元回归模型无法体现非线性特征[21];RBF神经网络模型具有通过学习逼近任意非线性映射的能力[22], 但其不准确的隐含层节点个数会影响逼近精度[23]。由遗传算法(GA)优化的RBF神经网络(GARBF神经网络)可以自适应地确定RBF神经网络隐含层节点个数[24],解决了RBF神经网络难以确定隐含层节点个数的缺陷,是预测土壤重金属空间分布的理想方法。
基于以上,本研究以黄河流域为研究区,以环境因子和土壤理化因子作为辅助变量,构建基于辅助变量的GARBF神经网络模型,开展土壤重金属空间分布预测,以期为黄河流域高精度土壤镉空间分布预测提供方法参考。
1 研究区概况与研究方法 1.1 研究区概况黄河流域位于32˚N ~ 42˚N、96˚E ~ 119˚E(图 1),自西向东横跨青藏高原、内蒙古高原、黄土高原、黄淮海平原,流经青海、四川、甘肃、宁夏、内蒙古、陕西、山西、河南、山东9个省(区),最后于山东省东营市垦利区注入渤海,流域面积约为7.95×105 km2。流域主要属于南温带、中温带和高原气候区,年均气温9 ℃,年降水量200 ~ 650 mm。土地利用类型主要有6种,占比从大到小依次为草地46.2%、耕地26.6%、林地13.6%、城镇3.1%、水体1.7%,其余为荒地。流域的土壤类型从上游到下游依次为栗钙土、黑垆土、褐土和潮土。在黄河流经的9省区中,2019年底常住总人口42 180.15万人,占全国的30.05%,地区生产总值约占全国25%,在我国社会经济发展中地位十分重要。
|
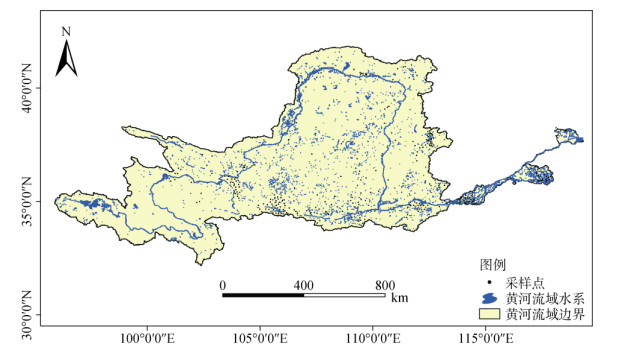
图 1 黄河流域土壤采样点分布 Fig. 1 Distribution of soil sampling sites in the Yellow River Basin |
本研究所采用的土壤重金属镉数据来自布置在黄河流域的329个土壤镉金属采样点(图 1)。在采样过程中,按照五点梅花采样法收集土壤,同时为减少人为扰动和表层污染积累的影响,确保土样中重金属镉含量的稳定性和代表性,采样深度设置为土壤表层5 ~ 15 cm,并利用手持GPS确定采样点经纬度坐标。采样完成后用聚乙烯密封袋避光保存,后将土样置于朝南风干室(严防阳光直射土样)进行自然风干,去掉石块、植物根茎等杂物后,研磨并过100目尼龙筛,装入干净密封袋备用。
参照HJ1315—2023《土壤和沉积物19种金属元素总量的测定电感耦合等离子体质谱法》[25],土壤镉含量的测定步骤大致为:称取0.2 g土壤放入微波消解罐中,分别加入9 mL HNO3(ρ=1.42 g/ml)、3 mL HCl(ρ=1.19 g/mL),充分混匀、反应平稳后,加盖拧紧,7 min内升温至120 ℃并保持3 min,消解完成后,冷却至室温;之后消解罐中内容物全部转移至坩埚,在坩埚中加入2 mL HF(ρ=1.16 g/mL),并将坩埚置于电热板上,120 ~ 140 ℃加热至内容物呈不流动的黏稠状,取下坩埚,冷却至室温,加入1 mL HClO4(ρ=1.67 g/mL),160 ~ 180 ℃继续加热至白烟几乎冒尽,内容物呈黏稠状;取下坩埚、稍冷,滴加少量稀硝酸溶液(1.41%)冲洗坩埚内壁,温热溶解内容物,冷却至室温后,转移至50 mL容量瓶中,待测。同时做空白试验。最后,利用电感耦合等离子体质谱仪(ICP-MS,Thermo Fisher,USA)进行测定。试验同时,制定标准溶液,建立标准曲线试验分析时均使用符合国家标准的优级纯试剂,试验用水为不含目标物的超纯水。
1.2.2 土壤理化因子数据本研究所采用的土壤理化因子数据来源于中国土壤信息格网基本属性数据集(国家地球系统科学数据中心土壤分中心:http://www.soil.geodata.cn),其空间分辨率为90 m,包含我国范围内基本土壤物理和化学属性。为确保获得的研究区土壤理化因子数据与实际土样采样点对应,核对采样点的经纬度、时间信息,选取数据集6个土层深度中的5 ~ 15 cm深度数据,从栅格数据中提取对应采样点的土壤pH、有机质含量(OM)、阳离子交换量(CEC)、黏粒含量数据集为土壤理化数据。
1.2.3 环境因子数据基于环境因子预测土壤属性是当前的主流技术,环境因子以地形因素和植被指数为主。黄河流域存在大面积的平原,地势平坦,地形因子对该区域的土壤重金属空间分布影响较小。因此,本研究仅选取归一化植被指数(NDVI)作为预测土壤镉空间分布的环境因子。NDVI由Landsat 8影像(影像日期为2022年01月01日)的第四、五波段在ArcGIS中进行栅格计算获取,Landsat 8数据下载自地理空间数据云(http://www.gscloud.cn)。为了与土壤理化因子数据集的空间分辨率保持一致,将NDVI数据的分辨率重采样至90 m。
1.3 研究方法 1.3.1 基于辅助变量的GARBF神经网络基于辅助变量的GARBF神经网络以辅助变量作为输入,以土壤镉作为网络输出,利用遗传算法(GA)对RBF神经网络的结构和权值进行优化。遗传算法具有全局逼近的能力,可避免神经网络陷入局部最优的问题。具体步骤如下:①二进制编码。隐含层与输出层之间的权值向量构成个体,对权值向量中的权值进行二进制编码,构成染色体。②初始化种群。进化以种群为单位,按照权值向量中各个权值范围,随机生成一定数量的权值向量,构成种群。③确定适应度函数。将训练样本点的数据代入由权值矩阵组成的神经网络,计算个体误差的绝对值(公式(1)),根据个体绝对误差确定适应度函数(公式(2),式中,
| $ E = \frac{1}{T}\sum\limits_{i = 0}^T {\left| {{y_i} - {{y'}_i}} \right|} $ | (1) |
| $ f(x) = \frac{1}{E} $ | (2) |
基于辅助变量的GARBF神经网络计算和建模均以Matlab为平台,运用其神经网络工具箱和遗传工具箱编程实现。
1.3.2 对照方法选用回归克里格和基于辅助变量的RBF神经网络作为研究的对照方法,分别探究相同辅助变量下,GARBF神经网络与前二者的预测精度差异;相同插值方法下,NDVI和不同土壤理化因子组合作为辅助变量对RBF和GARBF神经网络精度的影响。回归克里格预测土壤镉时,首先,利用多元逐步回归构建采样点辅助变量与土壤镉含量的回归方程,预测流域内土壤镉的空间分布;其次,对采样点预测残差进行普通克里格插值;最后,将土壤镉含量预测值和残差值叠加即获得研究区土壤镉含量。基于辅助变量的RBF神经网络以采样点辅助变量作为输入,以采样点镉含量作为网络输出,进行神经网络结构的训练,利用训练好的神经网络预测研究区土壤镉分布。
1.3.3 预测精度评价随机从329个土壤样点提取80%(263个)作为训练样本,其余20%(66个)作为检验样本,通过样本镉含量实测值与预测值之间的均方根误差(RMSE)、平均绝对误差(MAE)和平均相对误差(MRE)3个指标进行模型精度评价。
2 结果与分析 2.1 土壤镉含量描述性统计特征研究区329个采样点土壤中镉含量的平均值为0.75 mg/kg,范围为0.02 ~ 32.69 mg/kg,标准差为2.77 mg/kg (表 1)。土壤重金属镉的变异系数大于100%,说明土壤重金属镉的分布受外界因素的影响较大。从统计数据看,训练样本点与检验样本点大体上保留了全部采样点的结构特征。
|
|
表 1 土壤镉含量描述性统计 Table 1 Descriptive statistics of soil Cd content |
使用SPSS19.0进行土壤镉含量与其他理化因子的Pearson相关性分析(表 2),筛选与镉含量在P < 0.01水平上极显著相关的指标。从表 2可以看出,镉含量与黏粒含量相关性较弱,与OM、CEC呈显著正相关,与pH呈显著负相关,其中镉含量与CEC的相关性最高,相关系数为0.56,与OM、pH的相关系数分别为0.46、–0.48。因此,本研究选择pH、OM、CEC作为土壤镉含量的解释变量。
|
|
表 2 土壤镉含量与其他土壤理化性质的相关系数 Table 2 Correlation coefficients between soil Cd contents and other physio-chemical properties |
多个解释变量的共同作用可以增强或减弱对因变量的解释能力[26],将解释变量pH、OM、CEC进行不同组合,分别和环境因子NDVI作为神经网络模型的输入变量,比较不同输入变量下训练样本的逼近误差,筛选最优的土壤理化指标组合,结果如表 3所示。从表 3可以看出,仅基于NDVI而无土壤理化数据输入时的回归克里格、RBF神经网络和GARBF神经网络模型训练样本逼近误差最大,pH、OM、CEC的组合与NDVI作为回归克里格、RBF神经网络和GARBF神经网络模型输入的训练样本逼近误差最小。因此,选择pH、OM、CEC的组合和NDVI一起作为神经网络模型的辅助变量。
|
|
表 3 基于不同输入变量的训练样本误差 Table 3 Errors of the training samples based on different input variables |
将检测样本点带入回归克里格、RBF神经网络、GARBF神经网络模型,通过比较检测样本的误差,检验土壤理化因子和NDVI对神经网络模型预测精度的影响。表 4是不同辅助变量下3种预测方法检验样本的预测误差。检验样本误差反映方法的预测精度和可靠性,由检验样本的插值结果可以看出,基于pH、OM、CEC和NDVI的GARBF神经网络模型预测土壤镉的RMSE为0.173 mg/kg、MAE为0.131 mg/kg、MRE为18.9%,较基于相同辅助变量的RBF神经网络模型的RMSE、MAE、MRE分别降低0.009 mg/kg、0.005 mg/kg、0.6个百分点,说明遗传算法可以提高神经网络模型的预测精度;较基于相同辅助变量的回归克里格模型的RMSE、MAE、MRE分别降低0.003 mg/kg、0.002 mg/kg、0.2个百分点,说明基于辅助变量的GARBF神经网络模型预测精度高于回归克里格模型。由表 4还可知,在预测方法相同的情况下,以NDVI和pH、OM、CEC组合作为辅助变量的插值方法精度较高,以NDVI作为辅助变量的插值方法精度较低;在辅助变量相同的情况下,基于辅助变量的GARBF神经网络插值方法精度最高。上述结果表明,在NDVI的基础上,添加土壤理化因子作为辅助变量,可以提高神经网络模型的预测精度,遗传算法改进的神经网络方法(GARBF)具有更好的插值结果。
|
|
表 4 基于最佳输入变量的检验样本误差 Table 4 Errors of the testing samples based on best input variables |
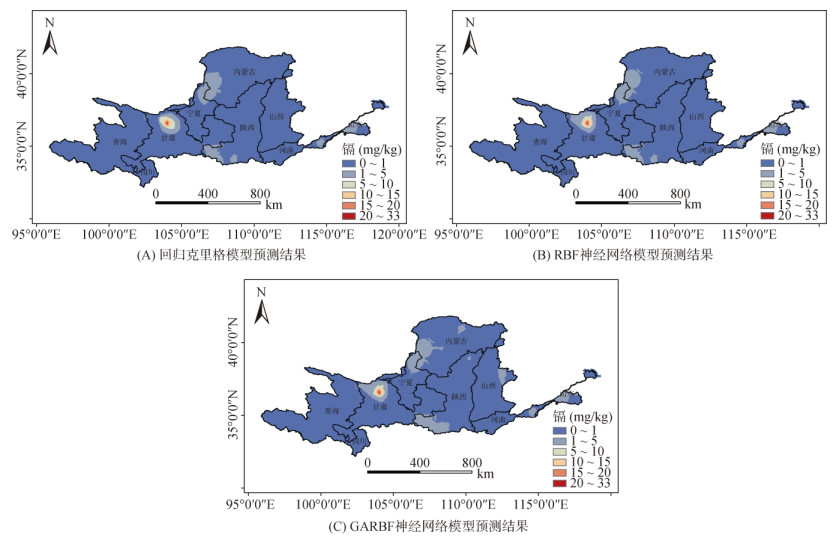
将最优变量组合的预测结果以相同分辨率的栅格格式在ArcGIS10.8中进行显示,如图 2所示。由图 2可以看出,各预测方法的土壤镉含量空间分布格局大体相同,土壤高含镉区域主要位于甘肃、陕西、内蒙古、宁夏、山东。其中,甘肃省白银市镉污染最为严重,这可能与该市支柱产业为有色重金属加工、冶炼[27]有关。李有文等[28]的研究也表明,白银市地表土壤中重金属镉的含量远远超过土壤背景值。与回归克里格、RBF神经网络模型预测结果相比,GARBF模型预测结果多出陕西榆林、山西省太原西部、内蒙古包头市西南部3处土壤高含镉区域,这3处区域的土壤镉含量在1 ~ 5 mg/kg。经资料分析发现,榆林地区采矿业以及太原钢铁冶炼工业均为当地经济支柱产业;包头市钢铁冶炼工业和稀土产业极为著名,有着“草原钢城”、“稀土之都”称号,且都集中分布在包头市西南部,这3种产业的生产过程均可能造成土壤重金属镉含量的升高。综上,基于土壤理化因子和NDVI的GARBF神经网络模型预测结果图更接近实际土壤重金属含量分布。
|
图 2 不同预测方法镉的空间分布 Fig. 2 Spatial distribution of cadmium in different prediction methods |
Mcbratney等[29]的研究证明,辅助变量数据可以提高神经网络模型对土壤重金属含量预测的准确性。为了准确预测土壤重金属含量的空间分布,应充分考虑影响土壤重金属分布的因素,筛选出获取简单、相关性强的辅助数据。除环境因子外,土壤理化因子中pH、OM、CEC与土壤中镉含量相关性较强、可以量化且容易获取。pH通过影响土壤中矿物质、水合氧化物等的表面负电荷来影响土壤对镉的吸附;OM具有大量的功能团,吸附镉的能力高于其他矿质胶体,且OM分解形成的小分子有机酸、腐殖酸等可以与镉形成稳定的络合物;而CEC反映胶体的负电荷量,CEC越高,负电荷量越高,吸附镉的能力越强。本研究显示,仅基于NDVI的神经网络模型预测精度最低,pH、OM、CEC分别单独与NDVI作为辅助变量均能提高神经网络模型的预测精度,pH、OM、CEC、NDVI共同作辅助变量时,神经网络模型的预测精度最高。
3.2 预测模型对比在辅助变量相同的情况下,GARBF神经网络模型的预测精度高于回归克里格模型和RBF神经网络模型。GARBF神经网络模型通过遗传算法优化了RBF神经网络模型隐层到输出层权值,从而降低了RBF神经网络模型的插值误差,使RBF神经网络具有更好的曲面逼近能力和全局寻优能力,因此遗传算法可以提高RBF神经网络模型的预测精度。回归克里格模型中的逐步多元回归计算过于简单,难以准确描述多个自变量与土壤镉之间的复杂非线性映射关系。此外,回归克里格模型中预测残差的克里格方法存在平滑效应。上述原因导致回归克里格模型预测精度较低。江叶枫等[30]也认为应用神经网络模型来代替回归克里格的预测方法和误差插值方法。
4 结论1) 基于土壤理化因子OM、pH、CEC和环境因子NDVI的RBF和GARBF神经网络模型的预测精度高于仅基于NDVI的RBF和GARBF神经网络方法;基于土壤理化因子和NDVI的回归克里格方法的预测精度高于仅基于NDVI的回归克里格模型。表明加入土壤理化因子(OM、pH、CEC)为辅助变量可以提升神经网络模型的预测精度。
2) GARBF神经网络模型通过遗传算法优化,在利用的辅助变量与RBF神经网络相同的情况下,GARBF神经网络模型的预测精度高于RBF神经网络模型;基于土壤理化因子OM、pH、CEC和环境因子NDVI的GARBF神经网络模型,通过遗传算法优化,其预测精度高于基于土壤理化因子(OM、pH、CEC)和NDVI的回归克里格模型。
3) 根据GARBF神经网络模型预测结果,黄河流域的土壤高含镉区域主要分布在甘肃白银市、陕西榆林市、内蒙古包头市西南部、山西太原市西部、内蒙古、宁夏、山东等地,与实际相符,表明基于土壤理化因子(OM、pH、CEC)和NDVI的GARBF神经网络模型预测黄河流域土壤镉空间分布具有较高的精度。
| [1] |
马娇阳, 保欣晨, 王坤, 等. 土壤镉污染的人体健康风险评价研究: 生物有效性与毒性效应[J]. 生态毒理学报, 2021, 16(6): 120-132 (  0) 0) |
| [2] |
Turgut C, Katie Pepe M, Cutright T J. The effect of EDTA and citric acid on phytoremediation of Cd, Cr, and Ni from soil using Helianthus annuus[J]. Environmental Pollution, 2004, 131(1): 147-154 DOI:10.1016/j.envpol.2004.01.017 (  0) 0) |
| [3] |
环境保护部, 国土资源部. 全国土壤污染状况调查公报[OL]. 2014-04-07. https://www.gov.cn/foot/site1/20140417/782bcb88840814ba158d01.pdf.
(  0) 0) |
| [4] |
骆永明. 中国土壤环境污染态势及预防、控制和修复策略[J]. 环境污染与防治, 2009, 31(12): 27-31 DOI:10.3969/j.issn.1001-3865.2009.12.021 (  0) 0) |
| [5] |
张云菲, 孜比布拉·司马义, 杨胜天, 等. 农田土壤重金属污染特征、生态风险评价与来源分析[J]. 江苏农业科学, 2020, 48(4): 266-272 (  0) 0) |
| [6] |
戴倩倩, 徐梦洁, 庄舜尧, 等. 基于地理探测器的封丘县农田土壤重金属分布影响因素研究[J]. 土壤, 2022, 54(3): 564-571 DOI:10.13758/j.cnki.tr.2022.03.017 (  0) 0) |
| [7] |
苗秀荣, 来雪慧, 李梦茜, 等. 不同钝化剂对土壤有效态重金属含量及其在小白菜中累积的影响[J]. 河南农业科学, 2020, 49(8): 63-71 (  0) 0) |
| [8] |
梅雪, 刘鸿雁, 吴龙华, 等. 基于HDXRF和ICP-MS的黔西北土壤重金属空间分布及影响因素研究[J]. 土壤, 2023, 55(2): 399-408 DOI:10.13758/j.cnki.tr.2023.02.021 (  0) 0) |
| [9] |
汪洁, 朱有为, 杨肖娥, 等. 农用地土壤可持续安全利用的研究与实践——以浙江省镉污染农田为例[J]. 土壤学报, 2023, 60(6): 1662-1674 (  0) 0) |
| [10] |
李启权, 王昌全, 岳天祥, 等. 基于定性和定量辅助变量的土壤有机质空间分布预测——以四川三台县为例[J]. 地理科学进展, 2014, 33(2): 259-269 (  0) 0) |
| [11] |
Li Q Q, Wang C Q, Dai T F, et al. Prediction of soil cadmium distribution across a typical area of Chengdu Plain, China[J]. Scientific Reports, 2017, 7(1): 7115 DOI:10.1038/s41598-017-07690-y (  0) 0) |
| [12] |
江叶枫, 郭熙. 基于多源辅助数据和神经网络模型的稻田土壤砷空间分布预测[J]. 环境科学学报, 2019, 39(3): 928-938 (  0) 0) |
| [13] |
周伟, 李丽丽, 周旭, 等. 基于地理探测器的土壤重金属影响因子分析及其污染风险评价[J]. 生态环境学报, 2021, 30(1): 173-180 (  0) 0) |
| [14] |
高中原, 肖荣波, 王鹏, 等. 融合自然-人为因子改进回归克里格对土壤镉空间分布预测[J]. 环境科学, 2021, 42(1): 343-352 (  0) 0) |
| [15] |
Ye H C, Huang W J, Huang S Y, et al. Effects of different sampling densities on geographically weighted regression Kriging for predicting soil organic carbon[J]. Spatial Statistics, 2017, 20: 76-91 DOI:10.1016/j.spasta.2017.02.001 (  0) 0) |
| [16] |
于灏, 苏智杰, 祝培甜, 等. 水稻、小麦与土壤中重金属Cd含量的关系模拟研究[J]. 地学前缘, 2021, 28(1): 438-445 (  0) 0) |
| [17] |
Micó C, Recatalá L, Peris M, et al. Assessing heavy metal sources in agricultural soils of an European Mediterranean area by multivariate analysis[J]. Chemosphere, 2006, 65(5): 863-872 DOI:10.1016/j.chemosphere.2006.03.016 (  0) 0) |
| [18] |
江叶枫, 郭熙, 叶英聪, 等. 基于辅助变量和神经网络模型的土壤有机质空间分布模拟[J]. 长江流域资源与环境, 2017, 26(8): 1150-1158 (  0) 0) |
| [19] |
尹群, 郭纪敏, 张世文, 等. 基于辅助变量的县域土壤有机质预测[J]. 江苏农业科学, 2020, 48(24): 267-273 (  0) 0) |
| [20] |
李保杰, 顾和和, 于法展, 等. 徐州市区土壤重金属空间分布研究[J]. 测绘科学, 2011, 36(5): 82–84, 89 (  0) 0) |
| [21] |
解雪峰, 濮励杰, 沈洪运, 等. 滨海重度盐碱地改良土壤盐渍化动态特征及预测[J]. 土壤学报, 2022, 59(6): 1504-1516 (  0) 0) |
| [22] |
柴杰, 江青茵, 曹志凯. RBF神经网络的函数逼近能力及其算法[J]. 模式识别与人工智能, 2002, 15(3): 310-316 (  0) 0) |
| [23] |
Wang G X, Gertner G, Parysow P, et al. Spatial prediction and uncertainty analysis of topographic factors for the Revised Universal Soil Loss Equation (RUSLE)[J]. Journal of Soil and Water Conservation, 2000, 55: 374-384 (  0) 0) |
| [24] |
董敏, 王昌全, 李冰, 等. 基于GARBF神经网络的土壤有效锌空间插值方法研究[J]. 土壤学报, 2010, 47(1): 42-50 (  0) 0) |
| [25] |
中华人民共和国生态环境部. 土壤和沉积物 19种金属元素总量的测定 电感耦合等离子体质谱法: HJ 1315—2023[S]. 北京: 中国标准出版社, 2023.
(  0) 0) |
| [26] |
Wang J F, Li X H, Christakos G, et al. Geographical detectors‐based health risk assessment and its application in the neural tube defects study of the Heshun Region, China[J]. International Journal of Geographical Information Science, 2010, 24(1): 107-127 (  0) 0) |
| [27] |
南忠仁, 李吉均, 张建明, 等. 白银市区土壤作物系统重金属污染分析与防治对策研究[J]. 环境污染与防治, 2002, 24(3): 170-173 (  0) 0) |
| [28] |
李有文, 曹春, 巨天珍, 等. 白银市不同区域蔬菜地土壤重金属污染特征及生态风险评价[J]. 生态学杂志, 2015, 34(11): 3205-3213 (  0) 0) |
| [29] |
McBratney A, Field D J, Koch A. The dimensions of soil security[J]. Geoderma, 2014, 213: 203-213 (  0) 0) |
| [30] |
江叶枫, 孙凯, 郭熙, 等. 基于环境因子和邻近信息的土壤属性空间分布预测[J]. 环境科学研究, 2017, 30(7): 1059-1068 (  0) 0) |
2. Henan Vocational College of Water Conservancy and Environment, Zhengzhou 450008, China;
3. Henan Geological Research Institute, Zhengzhou 450001, China
 2025, Vol. 57
2025, Vol. 57

