土壤有机质是维持土壤肥力和提高农业生产力的重要组成部分,对于农业可持续生产有着重要意义[1-2]。精确的有机质含量分布图是精细农业施肥、耕地质量建设、农田土壤固碳减排核算等工作的基础[3]。传统的土壤调查只能获得离散点位上的有机质含量,需要通过数字土壤制图的方式根据离散点位的有机质含量信息,预测未采样点的土壤有机质含量,获得有机质含量空间分布图,以指导农业生产[4]。
近几十年来,地统计学方法被普遍用来描述和预测土壤数据的空间分布,已有的研究表明地统计学是研究土壤空间分布的有效方法[5],普通克里格(OK)因其操作简便而成为最广泛使用的地统计学方法之一,但该方法对样点数量、样点分布要求严格,数据需满足地统计学相关假设,且未考虑到辅助变量对土壤属性的影响,其成图只能描述土壤属性的整体空间分布规律,对局部信息描述不够清晰[6-11]。反距离权重法(IDW)是基于相近相似原理[12],使用预测位置周围的测量值预测未采样位置的值,该方法同样未考虑辅助变量对土壤属性的影响。基于此,利用辅助变量进行土壤属性预测的方法逐渐发展。线性回归(LR)、回归克里格(RK)等综合多个变量对土壤属性进行空间插值,有效提高了预测精度,但土壤属性的强空间变异性使得全局模型无法很好地体现土壤属性的局部特征[13]。地理加权回归(GWR)作为一种局部回归模型,能充分解释土壤属性的局部空间关系和空间异质性[14]。地理加权回归克里格法(GWRK)将GWR与RK相结合,不但能体现土壤属性的局部特征,还有效反映土壤属性的空间自相关性,目前应用广泛[9, 15-16]。然而上述方法均是对变量的线性估计,土壤属性与环境变量间存在复杂的非线性关系[17],随机森林(RF)作为常用机器学习方法可有效解决土壤属性与环境变量之间的非线性问题,逐渐应用到土壤属性预测中,但受到环境变量选择的限制,对土壤属性精细的差异不能很好体现[18-21]。
各种数字制图模型各具特点,对于南亚热带岩溶区,高温高湿,地理条件特殊,如何选择模型及环境辅助变量来提高有机质含量预测精度是一个值得研究的课题。本文以典型南亚热带岩溶区为例,通过探索该区域不同类型环境变量,利用OK、RK、随机森林克里格(RFK)等8种预测模型对研究区土壤有机质含量进行空间分布预测制图,比较不同模型预测精度及差异,为南亚热带岩溶区精细制图方法的选取提供参考。同时,探索研究区域土壤有机质含量空间分布特征,为土壤属性空间变异研究提供依据。
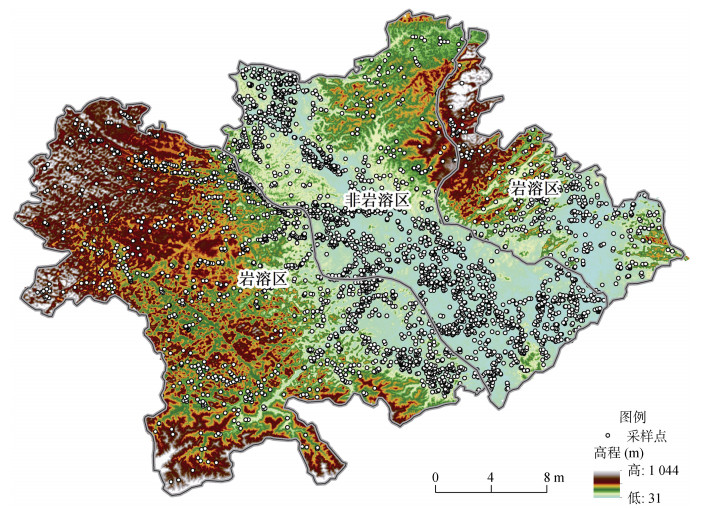
1 材料与方法 1.1 研究区概况研究区广西隆安县位于北回归线以南(107°18'E ~ 108°4'E, 22°51'N ~ 23°21'N),根据隆安县母岩母质图中石灰岩分布范围和LandSat遥感影像将隆安县划分为岩溶区和非岩溶区(图 1)。该研究区地势由东北、西和西南部向中部右江河谷逐渐倾斜;东北部为砂页岩丘陵和峰林石山组成,海拔为200 ~ 700 m;西南面以石灰岩峰丛洼地、峰丛谷地为主,海拔高度为300 ~ 700 m;中部为右江河谷,海拔高度多在200 m以下,属南亚热带季风气候的典型桂西南岩溶丘陵区。年平均降水量1 301 mm,年内降水量分配不均匀,季节性较强,降水多集中在夏季。多年平均气温21.8 ℃,多年平均最高月气温28.4 ℃,最低月平均气温13.2 ℃。
|
图 1 研究区高程与样点分布 Fig. 1 DEM and sampling sites in study area |
研究区耕地表层土壤有机质含量数据来自在研究区实施的“国家测土配方补贴资金项目”,2007—2009年共完成采样任务5 441个,采样深度0 ~ 20 cm,采集土壤样本的同时,记录采样点经纬度、高程、土壤类型、地貌类型等信息。剔除异常值及明显错误信息后,研究区有效样点4 013个,通过GIS软件对样点数据集进行均匀随机划分,获得训练集数据3 211个(80%),其中岩溶区样点1 582个,非岩溶区样点1 629个;验证集数据802个(20%),其中,岩溶区样点395个,非岩溶区样点407个。
1.2.2 环境变量数据获取为全面分析南亚热带岩溶区土壤有机质空间分布的环境变量影响情况。初步选择与土壤形成和有机质积累相关的22个因子作为研究区有机质含量空间预测的环境变量,本研究拟选取的环境变量信息及来源见表 1。
|
|
表 1 环境变量数据及来源 Table 1 Data and sources of environmental variables selected |
普通克里格(OK)是一种随机性局部插值法,用已知点的样本估计未知点的值,考虑变量的随机性。OK模型着重于空间自相关因素,用拟合的半变异直接进行插值。可表达为:
| $ z = \sum\limits_{i = 1}^n {{Z_i}{W_i}} $ | (1) |
式中:z为未知点的估计;Zi为i点的已知值;Wi为i点的权重;n为用于估算的已知点数。权重不仅与估算点和已知点之间的半变异有关,还与己知点之间的半变异有关。
1.3.2 回归克里格回归克里格(RK)模型是线性回归模型(LR)与OK模型的结合体,前者用来模拟解释变量与因变量的回归关系,即趋势项分布;后者用来探测观察值与预测值之差,即残差项的空间变异[15]。模型有两个特点,一是综合了各自变量对因变量的解释作用,二是在残差存在空间自相关的情况下对随机性变异进行解释。基本思路是:通过建立因变量与自变量之间的“最优”线性回归关系,得到代表确定性部分的趋势项与代表随机性部分的残差项,在残差存在空间自相关的情况下使用OK法对残差插值,最后将二者相加得到回归克里格插值结果[15]。
1.3.3 地理加权回归克里格地理加权回归克里格法(GWRK)是在地理加权回归(GWR)基础上扩展得到。GWR是基于普通最小二乘法原理的一种面向地理空间的建模方法,其特点在于将空间位置嵌入回归参数中,它在研究区域的每一处产生一个描述局部关系的回归模型。GWRK是对局部模型GWR拟合后得到的残差进行OK插值,该方法同时考虑了目标变量的空间异质性和空间自相关性[15-16]。基本思路是:通过对目标变量和辅助变量进行GWR拟合,得到局部回归的残差项,然后使用OK对所得残差项进行插值,将GWR预测值和OK插值误差相加得到预测结果。
1.3.4 随机森林随机森林(RF)是Breiman[22]提出的基于决策树的分类回归算法,它利用bootstrap重抽样方法从原始数据集中随机抽取多个样本,对每个样本数据进行决策树建模,然后组合成多棵决策树的预测模型,综合所有决策树的投票结果得到模型的预测值。基本思路是:从总样本中有放回地随机选出n个样本构建回归树,余下的样本作为袋外数据,袋外数据用来评价模型性能和自变量的重要性,通过投票或取平均值的方法得到回归树最终预测结果[23]。
1.3.5 随机森林克里格随机森林克里格(RFK)是一种结合了RF与OK的混合地统计方法,它考虑了变量间的非线性关系及目标变量的空间自相关性,提高了预测精度[6, 21]。通过RF算法得到的预测值与观测值之间存在残差,如果这些残差存在空间自相关性,可将残差当作随机变量,通过OK插值提高对未知点的预测精度。基本思路是:首先使用RF得到研究区有机质的预测值,计算RF预测残差,然后对预测残差进行OK插值,最后将RF预测值和OK插值误差相加得到预测结果。
1.4 环境变量筛选全局或局部线性回归模型,采用SPSS 22的相关性分析筛选出与土壤有机质显著相关的影响因子,使用逐步线性回归和方差膨胀因子(VIF)对环境变量之间的共线性进行检验。若VIF > 7.5,则移除相应的环境变量。随机森林模型,采用变量重要性函数importance()对解释变量进行筛选,将岩溶区重要性较弱的多年气温、曲率、平面曲率、坡向等变量剔除,非岩溶区重要性较弱的多年气温、EVI、RVI、NDVI等变量剔除。
1.5 预测模型精度评价本研究选用决定系数(R2)、均方根误差(RMSE)和平均绝对误差(MAE)3个指标对研究区耕地表层有机质空间预测输出结果的精度以及所选8种模型的性能表现进行评价。
| $ {R^2} = 1 - \frac{{\sum\limits_{i = 1}^n {{{\left( {{{\overset{\frown} y}_i} - {y_i}} \right)}^2}} }}{{\sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\bar y}_i}} \right)}^2}} }} $ | (2) |
| $ {\text{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\overset{\frown} y}_i}} \right)}^2}} } $ | (3) |
| $ {\text{MAE}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {{y_i} - {{\overset{\frown} y}_i}} \right|} $ | (4) |
式中:n代表采样点数量;
由土壤有机质含量的基本统计特征可知(表 2),全部数据集的有机质含量均值为35.94 g/kg,范围为7.6 ~ 101.9 g/kg,最大和最小值间差异显著。按照变异系数的划分等级:变异系数 < 10% 为弱变异,10% ~ 100% 为中等变异性、> 100% 为强变异性[24],岩溶区和非岩溶区均属中等变异。说明土壤有机质在该研究区范围内具有一定的变异性,适合空间局部估计。岩溶区训练集变异系数为41.82%,Moran I指数为0.65;非岩溶区训练集变异系数为34.72%,Moran I指数为0.23。空间相关性明显,岩溶区变异程度和空间相关性均强于非岩溶区。
|
|
表 2 土壤有机质含量的基本统计特征 Table 2 Basic statistical characteristics of SOM content |
根据土壤有机质与环境变量的相关性分析结果,Pearson相关性越大表示越相关。如表 3所示,岩溶区,与土壤有机质相关性显著的有土壤类型、土地利用类型、排水能力、灌溉能力、有机肥施用量、与居民点距离、坡度、化肥施用总量、剖面曲率、侵蚀模数、DVI、RVI、TWI、EVI、高程、多年降水、氮肥施用量;非岩溶区,与土壤有机质相关性显著的有土壤类型、氮肥施用量、土地利用类型、化肥施用总量、排水能力、灌溉能力、与居民点距离、有机肥施用量、高程、DVI、TWI、EVI。
|
|
表 3 土壤有机质含量与环境变量相关性统计 Table 3 Correlation coefficients between SOM content and environmental variables |
OK预测模型在ArcGIS 10.2软件中构建,因OK模型要求数据符合正态分布,通过剔除部分数据和对数变换后,数据符合正态分布,岩溶区和非岩溶区的块金效应分别为38.8% 和48.9%,存在中等程度空间相关性,可进行OK建模。
LR预测模型中,由于土壤类型和土地利用类型为类别变量,不能直接用于回归分析,通过算术平均值变换[25]将其转为数值型,算术平均值变换是以类别自变量各水平条件下定量因变量的算术平均值来代替类别自变量的一种方法。通过SPSS的逐步线性回归构建回归方程,使用ArcGIS 10.2的地图代数和克里格插值工具实现LR预测。LR模型以土壤类型、土地利用类型、高程等变量作为输入指标,岩溶区方程为:SOM=–105.038+土壤类型×0.723+土地利用类型×0.537+高程×0.024–有机肥施用量×0.005+灌溉能力×0.172+多年降水×0.057 +TWI×0.183;非岩溶区方程为:SOM=–12.731+土壤类型×0.564+氮肥施用量×0.566+土地利用类型×0.367–有机肥施用量×0.005+高程×0.024。
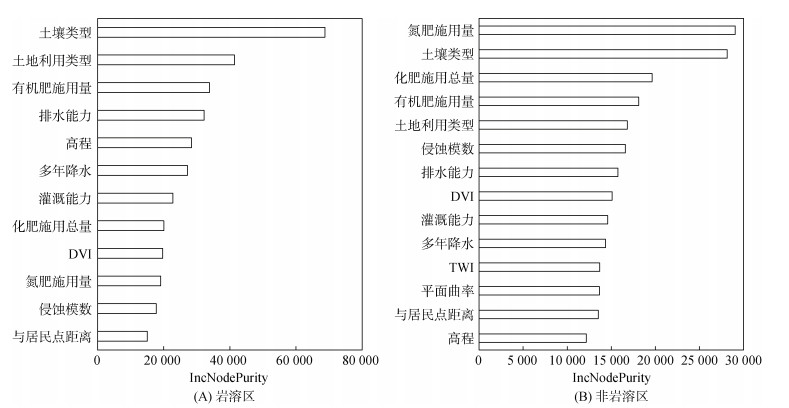
使用ArcGIS 10.2的地理加权回归工具实现GWR模型预测,GWR需去除局部共线性,通过去除VIF > 2.0的变量剔除模型的局部共线性。使用R语言构建RF模型,RF树节点的变量个数(mtry)和树的个数(ntree)是RF的两个重要参数,通过对不同个数辅助变量逐次计算袋外误差(OOB)确定出最优的mtry和ntree值,选择使用最优参数组合进行预测,岩溶区ntree为700、mtry为4;非岩溶区ntree为750,mtry为4。参与RF建模的解释变量相对重要性排序如图 2所示,其中IncNodePurity越大,环境变量越重要。从图 2可以发现,岩溶区的土壤类型、土地利用类型、有机肥施用量、排水能力、高程、多年降水、灌溉能力等是影响土壤有机质含量的主导因素。
|
图 2 RF预测模型中环境变量的重要性 Fig. 2 Importance of environment variables in random forest prediction model |
根据LR、GWR、RF的真实值与预测值之差计算残差,经分析,3个模型的残差均存在空间自相关性,对3个模型的残差进行OK插值,将插值结果与各模型预测值相加分别得到RK、GWRK、RFK的预测结果。不同预测模型的精度见表 4。从总体来看,岩溶区精度明显高于全域精度;全域和非岩溶区均为RK模型精度最高,R2分别为0.485和0.439,从面上看全域预测精度更高,这是由于全域预测中岩溶区域拟合程度较好,拉高了整体精度,单看全域预测中非岩溶区域精度R2仅为0.402,仍低于分区后非岩溶区精度。由此说明分区预测后,精度得到明显提高。
|
|
表 4 土壤有机质含量不同预测模型的精度 Table 4 Accuracies of different prediction models on SOM content |
岩溶区预测模型整体精度由高到低排序为RFK > RF > RK > GWRK > GWR > IDW > LR > OK,RFK精度最高,R2为0.572,由此说明地理环境复杂的岩溶区,更适合使用RFK模型。非岩溶区预测模型整体精度由高到低排序为RK > RFK > RF > LR > OK > GWRK > GWR > IDW,RK精度较高,R2为0.439,GWR和IDW的R2均小于0.300。该非岩溶区,样点主要集中在地势较低的河谷区域,虽地势平坦,但周边大部分为岩溶区,因特殊的地理条件限制,不建议使用IDW及OK预测模型。
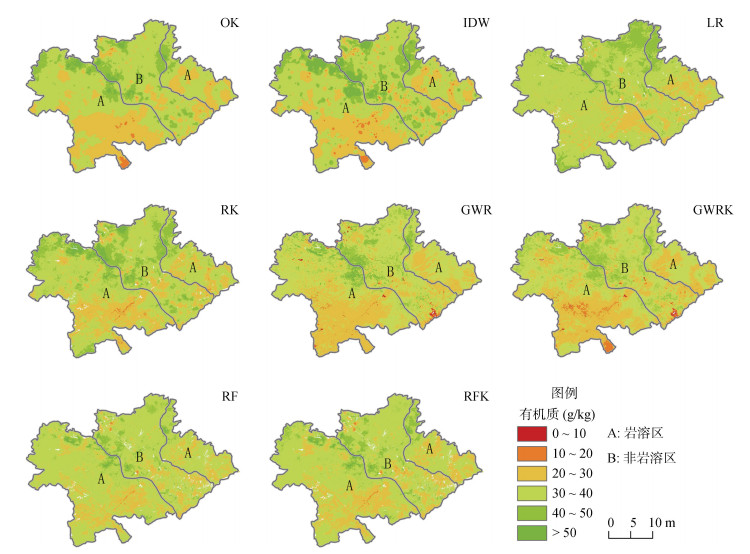
2.4 不同预测模型绘制空间分布图不同预测模型绘制的土壤有机质空间分布如图 3所示,土壤有机质分布的总体趋势基本一致,整体上非岩溶区有机质含量水平高于岩溶区;土壤有机质含量分布集中在20 ~ 40 g/kg,属于中等水平,高值主要集中分布在中北部的岩溶区与非岩溶区交界位置,低值主要集中在西南部。
|
图 3 不同模型预测的土壤有机质空间分布图 Fig. 3 Spatial distributions of SOM content predicted by different models |
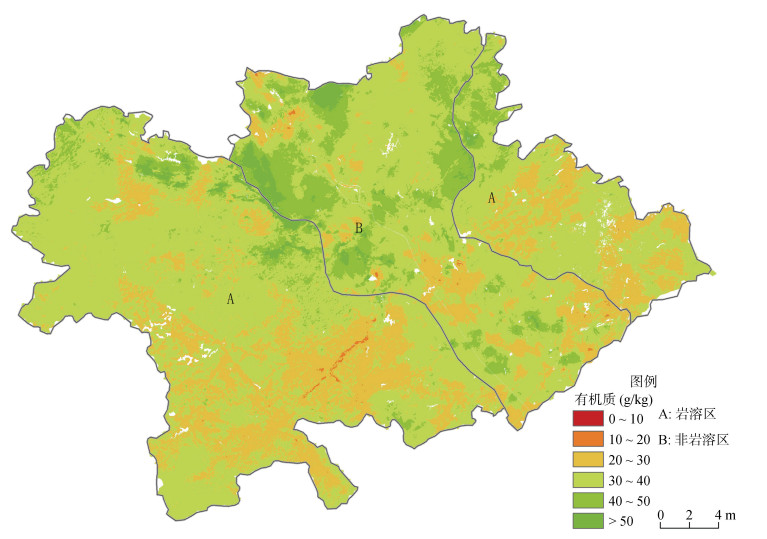
岩溶区,精度最低的OK预测模型绘制的空间分布图出现边界明显的块状区域,对于空间变异的细节信息描述不够详细;精度较高的RFK、RF、RK及GWRK预测模型在局部细节描述上更清晰,但对于土壤有机质的低值区间,因样点少预测结果体现不明显,由此说明RF和GWRK等预测模型在采样点有限的区域表现较差。非岩溶区,精度最低的IDW模型也出现明显的块状和点状区域。综上所述,岩溶区RKF预测精度最优,非岩溶区RK预测精度最优。将岩溶区的RKF预测结果与非岩溶区RK预测结果使用镶嵌工具合并形成土壤有机质空间分布图(图 4)。
|
图 4 土壤有机质含量预测结果镶嵌图(岩溶区RKF预测,非岩溶区RK预测) Fig. 4 Mosaic map of predicted SOM content (RKF for karst region, RK for non-karst region) |
根据随机森林相对重要性排序,岩溶区的土壤类型、土地利用类型、有机肥施用量、排水能力、多年降水、高程、灌溉能力等是影响土壤有机质含量的主导因素。这是由于不同成土过程形成的土壤类型以及不同的土地利用方式都会导致土壤理化性质差异较大;岩溶区域不同高程对土壤所处的气候环境具有调控作用,土壤有机质的分解和积累影响明显[26];同时,岩溶区域受多年降水、灌溉及排水等影响,都会加剧岩溶区的溶蚀作用,导致土壤有机质在坡地流失而在低洼区域积累[27-29]。因此,相比非岩溶区,岩溶地区土壤有机质分布具有较强的空间异质性。
3.2 土壤有机质空间分布及其影响因素。从土壤有机质空间总体分布来看,研究区土壤有机质含量呈现中北部高、西南部低的空间分异特征。从分区来看,非岩溶区有机质含量整体高于岩溶区。非岩溶区土壤有机质含量集中在30 ~ 50 g/kg,北部为土山,中部和东南部为河谷地带,地理条件较好,为隆安县主要的粮食产区,受人为灌溉、施肥、秸秆还田等影响,土壤有机质含量较高,土壤较肥沃。岩溶区域,土壤有机质含量大部分区域集中在20 ~ 40 g/kg,属于中等水平;该区域海拔相对较高,多为坡地,特别是西南部和东部区域,受到基岩出露及降雨等影响,植被覆盖度低,存在一定的水土流失和迁移,导致养分流失,因此在岩溶地区土壤有机质含量相对较低。
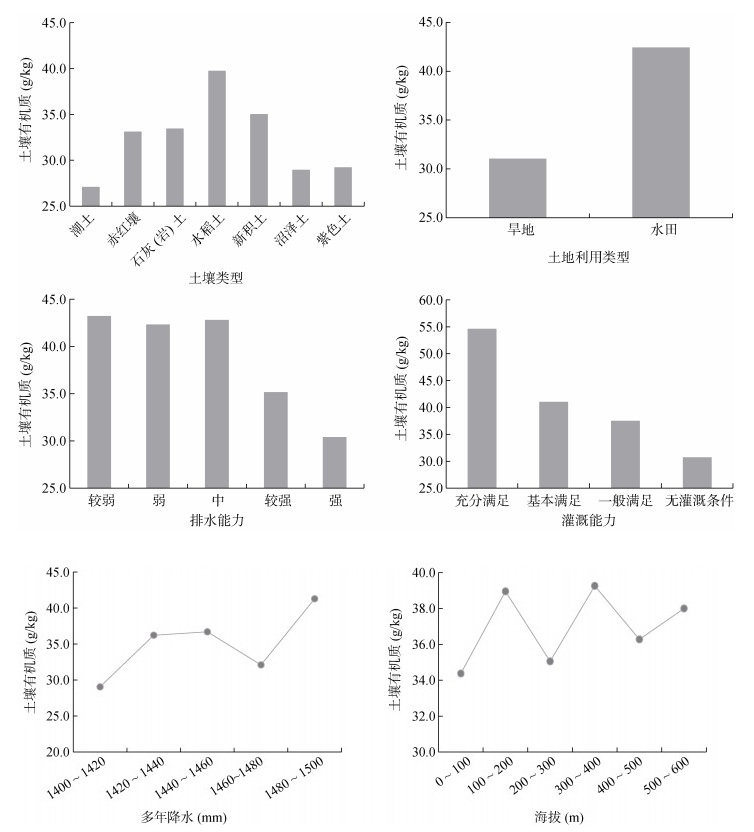
通过比较土壤类型、土地利用类型、排水能力、多年降水、灌溉能力及海拔等环境变量与土壤有机质的关系可知(图 5),水稻土的土壤有机质含量最高,为39.72 g/kg,主要集中分布在中部河谷区;潮土和紫色土的土壤有机质含量较低,潮土主要为潮砂土,该土壤类型易漏水漏肥;紫色土面积不大,主要分布在非岩溶区北部,属于易风化易侵蚀的一种土壤类型,其表土层薄、土质疏松结构性差,土壤养分易流失。水田的土壤有机质含量明显高于旱地,这主要是受稻田淹水影响,产生还原环境,有利于缓解土壤有机质矿化分解,增加土壤有机质积累[30]。土壤有机质与多年降水、灌溉能力趋于正相关,与排水能力趋于负相关,由此说明灌溉条件越好、降水量充沛、适中的排水条件,更有利于土壤有机质积累。从海拔来看,土壤有机质与海拔关系呈现M型,海拔0 ~ 100 m主要为中部的河谷区,受人为耕作影响,有机质积累与流失同步进行;海拔100 ~ 200 m为岩溶区的低洼区域以及北部岩溶区与非岩溶区交界地带,海拔300 ~ 400 m为岩溶区西北部的低洼区域,土壤有机质相对较高,这是由于岩石溶蚀过程形成的可溶性碳酸盐与土壤腐殖质结合、凝聚,形成稳定的腐殖酸钙,极有利于土壤有机质的累积[22-23],导致土壤有机质在这些低洼区域积累;海拔200 ~ 300 m和400 ~ 500 m均为岩溶区的坡地,受岩溶区基岩出露及植被覆盖度低等特殊地理环境影响,土壤发育缓慢,形成的土层较为浅薄,土壤总量较少,相应的土壤有机质含量也较少[24]。
|
图 5 主导环境变量下土壤有机质含量 Fig. 5 SOM contents under dominant environmental variables |
研究认为非岩溶区虽然成土环境相对单一,但不推荐使用OK模型,这与李梦佳等[6]在不同模型预测土壤有机质含量空间分布对比分析中提到的观点不一致,一般认为成土环境相对单一区域,OK模型预测结果精度较高。由于本研究的非岩溶区大部分位于河谷,水系发达,在成土过程中受到周边岩溶区影响较大,仅依靠采样点数据进行插值的OK模型,将忽略重要环境变量对土壤有机质的影响,不推荐直接使用OK模型预测,推荐使用RK等环境变量与地统计相结合的模型预测土壤有机质空间分布。岩溶区地理环境特殊,特别是受到土壤类型、土地利用类型以及水分影响,单纯的地统计模型已不适用,推荐使用RFK与地统计相结合的模型进行预测。
从模型精度来看,岩溶区域整体预测精度明显高于非岩溶区,岩溶区最优模型RFK的R2为0.572、非岩溶区最优模型RK的R2为0.439,这可能与环境变量的选择有关。尽管本研究已收集了各类环境变量,并对环境变量进行筛选,大大降低数据冗余,但环境变量的选取还存在考虑不周全的问题。非岩溶区域作为主要的粮食产区,受人为干扰明显大于岩溶地区,如秸秆还田、种植绿肥、耕作制度等都会影响土壤有机质含量,但这类人为因素在本文中考虑较少,因此,对于非岩溶区与土壤有机质相关的环境变量还需要继续挖掘。
4 结论1) 岩溶区土壤有机质的变异程度和空间相关性均强于非岩溶区。岩溶区土壤有机质主要受土壤类型、土地利用类型、有机肥施用量、排水能力、多年降水、高程、灌溉能力等因素影响。
2) 相较于全域模型,分区建模显著提升了土壤有机质的预测精度,其中岩溶区模型精度明显高于非岩溶区。对比8种模型,岩溶区RFK为最优模型,R2为0.572;非岩溶区最优模型为RK,R2为0.439。研究发现预测模型LR、GWR和RF的残差进行OK插值后,模型精度得到提高,表明在预测建模时需集成土壤有机质的空间自相关特征以提高制图精度。
3) 单纯的地统计模型已不适用于岩溶区,使用RFK与地统计相结合的模型可有效提高土壤有机质的预测精度;非岩溶区虽成土环境相对单一,但受周边岩溶区影响,仅使用OK模型无法很好表征土壤有机质空间分布情况,推荐使用RK与地统计相结合的模型预测。
| [1] |
王欣怡, 王昌昆, 马海艺, 等. 基于双时相卫星遥感光谱指数估算土壤有机质含量[J]. 土壤, 2023, 55(5): 1106-1113 (  0) 0) |
| [2] |
李丹, 王京文, 李凤根, 等. 1982—2012年来杭州市郊水稻田有机质变化特征及其调控措施[J]. 水土保持通报, 2016, 36(3): 131-135 (  0) 0) |
| [3] |
Wang Y Q, Zhang X C, Zhang J L, et al. Spatial variability of soil organic carbon in a watershed on the Loess Plateau[J]. Pedosphere, 2009, 19(4): 486-495 (  0) 0) |
| [4] |
王雨雪, 杨柯, 高秉博, 等. 基于两点机器学习方法的土壤有机质空间分布预测[J]. 农业工程学报, 2022, 38(12): 65-73 (  0) 0) |
| [5] |
孟博, 周一帆, 杨林生, 等. 勐海县甘蔗土壤养分空间分布特征及肥力评价[J]. 土壤, 2022, 54(2): 277-284 (  0) 0) |
| [6] |
李梦佳, 王磊, 刘洪斌, 等. 不同模型预测土壤有机质含量空间分布对比分析[J]. 西南农业学报, 2021, 34(3): 610-617 (  0) 0) |
| [7] |
陆访仪, 赵永存, 黄标, 等. 海伦市耕层土壤有机质含量空间预测方法研究[J]. 土壤通报, 2012, 43(3): 662-667 (  0) 0) |
| [8] |
石光辉, 毛伟, 曾洪玉, 等. 扬州市江都区耕地土壤有机质35年变化特征及其影响因素分析[J]. 扬州大学学报(农业与生命科学版), 2022, 43(6): 44-50 (  0) 0) |
| [9] |
杜佩颖, 张海涛, 郭龙, 等. 平原丘陵过渡区土壤有机质空间变异及其影响因素[J]. 土壤学报, 2018, 55(5): 1286-1295 (  0) 0) |
| [10] |
张欢, 高小红. 复杂地形区土壤有机质空间变异性分析及制图[J]. 水土保持研究, 2020, 27(5): 93-100 (  0) 0) |
| [11] |
姜赛平, 张怀志, 张认连, 等. 基于三种空间预测模型的海南岛土壤有机质空间分布研究[J]. 土壤学报, 2018, 55(4): 1007-1017 (  0) 0) |
| [12] |
马利芳, 熊黑钢, 孙迪, 等. 不同干扰程度下土壤有机质空间最优插值法研究[J]. 生态学报, 2019, 39(19): 7153-7160 (  0) 0) |
| [13] |
姚雪玲, 傅伯杰, 吕一河, 等. 基于GIS和统计模型的黄土丘陵沟壑区土壤水分插值方法[J]. 水土保持学报, 2013, 27(6): 93–96, 102 (  0) 0) |
| [14] |
王幼奇, 张兴, 赵云鹏, 等. 基于GIS和地理加权回归的砂田土壤阳离子交换量空间预测[J]. 土壤, 2020, 52(2): 421-426 (  0) 0) |
| [15] |
杨顺华, 张海涛, 郭龙, 等. 基于回归和地理加权回归Kriging的土壤有机质空间插值[J]. 应用生态学报, 2015, 26(6): 1649-1656 (  0) 0) |
| [16] |
李运龙, 熊立华, 闫磊. 基于地理加权回归克里金的降水数据融合及其在水文预报中的应用[J]. 长江流域资源与环境, 2017, 26(9): 1359-1368 (  0) 0) |
| [17] |
李豪, 刘涛, 徐精文. 基于混合地理加权回归与克里格的区域降水量空间插值方法[J]. 中国农业气象, 2018, 39(10): 674-684 (  0) 0) |
| [18] |
任丽, 杨联安, 王辉, 等. 基于随机森林的苹果区土壤有机质空间预测[J]. 干旱区资源与环境, 2018, 32(8): 141-146 (  0) 0) |
| [19] |
韩杏杏, 陈杰, 王海洋, 等. 基于随机森林模型的耕地表层土壤有机质含量空间预测——以河南省辉县市为例[J]. 土壤, 2019, 51(1): 152-159 (  0) 0) |
| [20] |
凌晓丹, 王罗其, 赵科理, 等. 基于随机森林法的山核桃林地土壤速效养分含量空间分布特征研究[J]. 生态学报, 2024, 44(2): 662-675 (  0) 0) |
| [21] |
马重阳, 孙越琦, 巫振富, 等. 基于不同模型的区域尺度耕地表层土壤有机质空间分布预测[J]. 土壤通报, 2021, 52(6): 1261-1272 (  0) 0) |
| [22] |
Breiman L. Random forests[J]. Machine Learning, 2001, 45(1): 5-32 (  0) 0) |
| [23] |
Cutler A, Cutler D R, Stevens J R. Random forests[M]// Ensemble machine learning. New York: Springer, 2012: 157–175.
(  0) 0) |
| [24] |
秦静, 孔祥斌, 姜广辉, 等. 北京典型边缘区25年来土壤有机质的时空变异特征[J]. 农业工程学报, 2008, 24(3): 124–129, 314 (  0) 0) |
| [25] |
胡良平. 提高回归模型拟合优度的策略(Ⅱ)——算术均值变换与其他变量变换[J]. 四川精神卫生, 2019, 32(1): 9-15 (  0) 0) |
| [26] |
李洪义, 贺任彬, 谢模典, 等. 自然和人为因素对耕地土壤有机质含量影响的研究[J]. 土壤通报, 2023, 54(5): 1050-1059 (  0) 0) |
| [27] |
欧阳资文, 彭晚霞, 宋同清, 等. 喀斯特峰丛洼地土壤有机质的空间变化及其对干扰的响应[J]. 应用生态学报, 2009, 20(6): 1329-1336 (  0) 0) |
| [28] |
邸欣月, 安显金, 董慧, 等. 贵州喀斯特区域土壤有机质的分布与演化特征[J]. 地球与环境, 2015, 43(6): 697-708 (  0) 0) |
| [29] |
文鑫, 王艺惠, 钟聪, 等. 贵州表层土壤有机质空间变异特征及其影响因素分析[J]. 水土保持学报, 2023, 37(3): 218-224 (  0) 0) |
| [30] |
李冬初, 黄晶, 马常宝, 等. 中国稻田土壤有机质时空变化及其驱动因素[J]. 中国农业科学, 2020, 53(12): 2410-2422 (  0) 0) |
 2025, Vol. 57
2025, Vol. 57


