2. 教育部东北多年冻土区地质环境系统野外科学观测研究站, 东北林业大学, 哈尔滨 150040;
3. 水利部江河源区水生态治理与保护重点实验室, 青海大学, 西宁 810016;
4. 湖南省城市地下基础设施结构安全与防灾工程研究中心, 湖南城市学院, 湖南益阳 413002;
5. 湖南省数字化城乡空间规划关键技术重点实验室, 湖南城市学院, 湖南益阳 413002;
6. 黑龙江省高校防灾减灾工程与防护工程重点实验室, 东北石油大学, 黑龙江大庆 163318;
7. 教育部结构灾变与控制重点实验室, 哈尔滨工业大学, 哈尔滨 150040
东北黑土地作为我国重要的商品粮基地和生态安全屏障,在保障国家粮食安全和生态稳定方面发挥着不可替代的作用[1-2]。该区域具有显著的季节性冻融特征,冻融水力复合侵蚀现象普遍存在。土壤在冻融过程中,其剖面水热状态发生复杂耦合变化,导致土壤含水量重新分布[3-4],这不仅直接影响次年地表水文条件,改变土壤水分供应,进而影响春季农作物的生长和生产力,还会加剧水土流失,威胁区域生态安全[5]。因此,深入研究黑土冻融过程具有重要的现实意义。
目前,学者在黑土冻融领域研究广泛。研究方法上,布设分布式温湿度传感器阵列与三维激光扫描系统,连续监测不同冻结强度梯度(–5 ~ –15 ℃)、多样土地利用类型(农田、林地、退化草地)及积雪、秸秆覆盖下黑土坡面水热动态[6-8];借助扫描电镜(SEM)、CT断层扫描和数字图像相关技术(DIC),在室内模拟装置中捕捉团聚体单向冻融循环(0.5 ~ 2 ℃/h温变速率)时孔隙结构演变与应变场分布[1, 9-11],特别关注冰透镜体生长引发的应力集中效应[9-12]。理论分析上,融合分形几何与非平衡态热力学原理,构建多相耦合冻融动力学模型[12-13];引入相场模型描述水冰相变界面动力学[14-15],结合改进Richard方程耦合热传导方程,提高冻融锋面移动模拟精度[16-19]。然而,受试验条件和理论模型局限性的制约,现有研究仍存在一定局限:传统传感器阵列(空间分辨率≥5 cm)难以捕捉黑土剖面毫米级异质层结中的水热突变特征[20-22];现有模型对冰透镜体生长与土壤结构变形间的双向反馈机制刻画不足[23-24];相场模型参数化过程未充分考虑黑土胶体–冰晶界面能各向异性特征等[25-26]。这些局限性导致在非均匀初始含水率(> 30%)或快速冻结(降温速率 > 1 ℃/h)下模拟误差超过15%[14, 27]。这在很大程度上限制了对冻融水力复合侵蚀过程机制的深入研究。
鉴于此,本研究选取东北典型黑土区土壤作为研究样本,采用室内单向冻结土柱模拟试验,在评估冻土水热耦合模型适用性的基础上,构建热–水–形变多物理场耦合控制方程体系,对不同冻结温度、初始温度、初始含水量和补水条件下黑土水热迁移规律及团聚体输移破碎宏微观形变特征进行深入剖析。研究成果将为黑土冻结水热运移规律分析提供技术支持,为进一步认识该区域土壤冻融侵蚀过程机制提供理论依据。
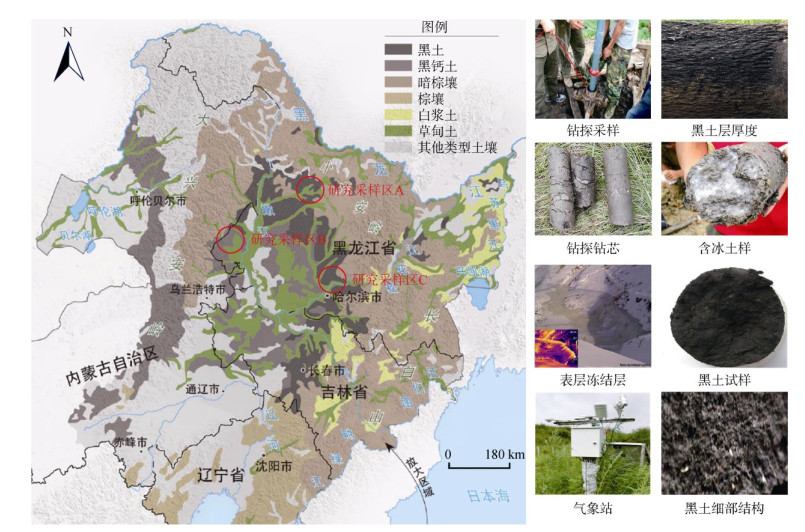
1 材料与方法 1.1 研究区概况选取东北黑土带沿经度梯度分布的3个典型区域为研究区(图 1):黑河市孙吴县(A区,寒温带过渡区,127°18′21″E ~ 127°21′06″E,49°30′52″N ~ 49°33′46″N)、齐齐哈尔市克山县(B区,温带核心耕作区,125°11′26″E ~ 125°18′33″E,48°16′25″N ~ 48°20′17″N)及哈尔滨市香坊区(C区,暖温带城市化影响区,126°43′36″E ~ 126°46′22″E,45°43′56″N ~ 45°46′21″N),形成纬度跨度达3.9°的梯度观测网络(图 1)。研究区覆盖黑土典型亚类(厚层黑钙土、普通黑土、草甸黑土),其土壤发育年龄(8 000 ~ 12 000 a)、有机质含量(38 ~ 62 g/kg)及黏粒矿物组成(2∶1型黏土矿物占比58% ~ 73%),具有显著区域分异特征[14, 25-26]。研究区年均冻融循环次数达25 ~ 38次,最大冻深梯度呈现北纬递增规律(A区218 cm > B区182 cm > C区156 cm)[14, 24-26]。
|
图 1 黑土研究区位置及钻探样品 Fig. 1 Locations of study areas and drilling samples for black soil |
研究区受西伯利亚高压(冬季平均风速4.2 ~ 5.8 m/s)与夏季东南季风(水汽通量8 ~ 12 g/(cm·hPa·s))双重控制,形成极端季节性气候:冻结期(11月15日—3月20日)土壤热扩散系数骤降43% ~ 67%,日均负温持续时间 > 16 h,冻胀率与融沉系数分别达0.8% ~ 1.5% 和1.2% ~ 2.1%[5, 14, 26]。供试粉质黏土(USDA分类)液塑限分别为32.5% 和18.7%,阳离子交换量(CEC)28.4 cmol/kg,体积热容量1.68 MJ/(m3·K),其孔隙结构呈现双峰分布特征(< 2 μm微孔隙占41%,50 ~ 200 μm大孔隙占29%)。降水时空异质性显著(变异系数0.38 ~ 0.51),汛期(6—9月)降水强度指数(PCI)达18.7 ~ 22.4,导致冻结前土壤体积含水量(θv)达20% ~ 31%,为冻胀水分迁移提供充足势能梯度(基质势差Δψ达–85 ~ –112 kPa)[14, 26-27]。另外,基于2021—2024年冻融季前分层采样数据(0 ~ 50 cm深度,每10 cm取样),3个研究区表层土壤(0 ~ 20 cm)初始体积含水量呈现显著空间差异:A区厚层黑钙土持水性强(θv=20.3%±1.8%),B区耕作扰动增强入渗(θv= 25.7%±2.1%),C区受城市热岛效应的影响产生水分滞留(θv =29.4%±1.5%)(n=45,烘干法测定,置信度95%)[27-29]。该实测梯度为试验参数设计提供基准。
1.2 试验设计 1.2.1 野外监测试验在黑土区典型侵蚀沟发育区布设3组野外综合观测单元,每个单元包含:①梯度气象观测系统,采用GD24-YCXQ型微型气象站(安装高度2.5 m)(图 1),同步监测气温(±0.3 ℃)、风速(±0.3 m/s)、降水量(±0.2 mm)等气象要素,时间分辨率15 min;②冻融锋面监测系统,沿垂直剖面布设PT100地温链(测温深度0 ~ 150 cm,间距10 cm),结合自主研发的冻胀位移计(分辨率0.01 mm),实现冻融锋面运移轨迹的动态捕捉;③水热通量观测系统,按坡面形态配置热流板阵列(HFP01SC,精度±5 W/m2),采用嵌套式布设方案(主测点间距50 m,辅测点间距100 m),通过三维水热通量观测网络获取坡面尺度冻融水热传输特征。
1.2.2 地质钻探试验在研究区A布设4组地质钻孔,采用XY-180型岩芯钻机(取芯率≥90%)实施分层取样。钻孔间距沿侵蚀沟走向呈扇形分布(间距200 m),取样深度0 ~ 8 m,按土层突变界面加密采样(垂向间隔0.5 m)。原位参数测定:采用TDR-315型水分速测仪(±1.5%)测定体积含水量,通过双环入渗法获取渗透系数(10–5 ~ 10–3 cm/s量级)。岩芯实验室分析:利用激光粒度仪(Mastersizer 3000)测定粒径分布,X射线衍射分析矿物成分。
1.2.3 室内模拟试验在典型黑土层按梅花形布点采集原状土样,经自然风干、筛分(剔除 > 2 mm粗颗粒)制备均质试样。采用分层击实法控制容重(1.25 ~ 1.45 g/cm³)并预埋TDR探针(CS650,精度± 2%),建立初始含水率(20%、25%)与温度梯度(–5、–10、–15 ℃)的6组正交试验(UFBS-1~ UFBS-6)。试件采用专利设计的双层有机玻璃柱(直径10 cm×高15 cm),通过PID温控系统实现顶板梯度降温(精度± 0.5 ℃)与底板恒温(3 ℃),沿试样深度方向(3、6、12 cm)布设Pt100温度传感器阵列(±0.1 ℃)与水分特征曲线测定系统。
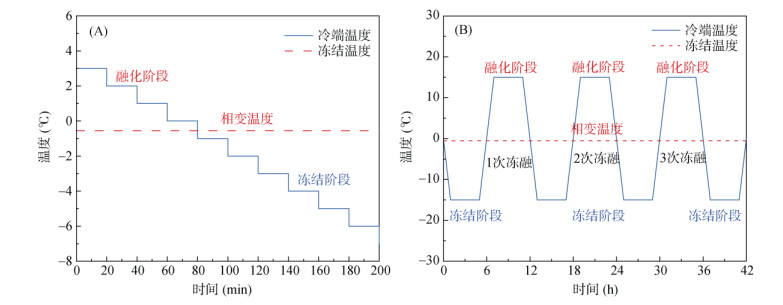
本次试验试样的具体参数见表 1。另外,为探究特定稳定负温情境下土壤温度与未冻水含量之间的内在关联,本文运用小梯度降温的试验手段(图 2A),可更准确地捕捉土壤在稳定负温下温度与未冻水含量之间的微观联系。
|
|
表 1 试验参数设计 Table 1 Experimental parameter design |
|
(A. 单向冻结温度变化曲线;B. 冻融循环温度变化曲线) 图 2 单向冻结及冻融循环温度边界曲线 Fig. 2 Temperature boundary curves for unidirectional freezing and freeze-thaw cycles |
为进一步研究冻融循环作用下,不同初始条件(含水率、温度、补水情况)对黑土水热–变形协同作用的影响,设计6组冻融循环试件(CFBS-1 ~ CFBS-6),开展黑土冻融循环的理论模型分析,模型参数如表 1所示。试件顶端温度Tu(t) 处于动态变化(图 2B),底端温度保持恒定。
1.3 理论模型分析 1.3.1 基本假定将土体设定为各向同性且连续分布的介质,其变形符合小应变条件下线弹性规律,土颗粒和冰均为不可压缩体。在土体冻结阶段,对水分迁移的分析侧重于液态水的迁移过程,以此简化分析模型,同时保证在一定精度范围内对土体冻结特性的有效描述与研究,从而为相关问题提供理论基础与实践指导,确保在涉及土体冻结情况时的稳定性。
1.3.2 温度场控制方程以傅里叶定律为热传导分析基础理论,在二维水热耦合下,将相变潜热纳入热源项,推导出冻土热传导微分方程如下:
| $ \rho C(\theta )\frac{{\partial T}}{{\partial t}} = \lambda (\theta ){\nabla ^2}T + L \cdot {\rho _{\text{I}}}\frac{{\partial {\theta _{\text{I}}}}}{{\partial t}} $ | (1) |
式中:▽为微分算子,对于二维问题为[∂/∂x,∂/∂y],x,y为水平和深度方向坐标(m);T为土体的瞬态温度(℃);t为时间(s);θ为体积含水率(%),θI为孔隙冰体积含量(%);ρ、ρI为土和冰的密度(kg/m3);L为相变潜热,取值为334.5 kJ/kg;λ(θ)为导热系数(W/(m·℃));C(θ)为体积热容(J/(kg·℃))。
1.3.3 水分场控制方程在冻土水分迁移研究中,鉴于其与融土在水分迁移规律上存在一定相似性,以融土水分运动规律为基础,考虑水冰相变因素,推导出能够描述冻土中水分迁移的Richards方程:
| $ \frac{{\partial {\theta _{\text{u}}}}}{{\partial t}} + \frac{{{\rho _{\text{I}}}}}{{{\rho _{\text{w}}}}}\frac{{\partial {\theta _{\text{I}}}}}{{\partial {\text{t}}}} = \nabla \left[ {D\left( {{\theta _{\text{u}}}} \right)\nabla {\theta _{\text{u}}} + k\left( {{\theta _{\text{u}}}} \right)} \right] $ | (2) |
式中:θu为冻土中未冻水的体积含量(%);ρW为水的密度(kg/m3);D(θu)为冻土中未冻水的扩散率;k为重力加速度方向的非饱和土体渗透系数;总体积含水量为θt=θu+ρI/ρw·θI(kg/m3)。
鉴于冰晶会对水流造成显著的阻塞作用,D(θu)计算如下:
| $ D\left( {{\theta _{\text{u}}}} \right) = \frac{{k\left( {{\theta _{\text{u}}}} \right)}}{{c\left( {{\theta _{\text{u}}}} \right)}} \cdot I $ | (3) |
| $ k\left( {{\theta _{\text{u}}}} \right) = {k_{\text{s}}} \cdot {S^l}{\left( {1 - {{\left( {1 - {S^{1/m}}} \right)}^m}} \right)^2} $ | (4) |
| $ c\left( {{\theta _{\text{u}}}} \right) = {a_0}m/(1 - m) \cdot ({\theta _{\text{s}}} - {\theta _{\text{r}}}) \cdot {S^{1/m}}{\left( {1 - {S^{1/m}}} \right)^m} $ | (5) |
| $ I = {10^{ - 10{\theta _{\text{I}}}}} $ | (6) |
式中:k(θu) 为土体渗透率(m/s);c(θu) 为比水容量(1/m);I为土中冰对水分迁移阻碍作用的阻抗因子;S为饱和度;m、l、a为VG模型参数;ks为饱和土渗透系数(m/s);θs为饱和含水率(cm3/cm3);θr为残余含水率(cm3/cm3);θI为孔隙冰体积含量(%)。
1.3.4 位移场控制方程在线弹性假设条件下,应力与应变呈现线性正相关关系,其具体表达式如下:
| $ - \nabla \cdot \sigma = F $ | (7) |
| $ \varepsilon = \nabla u $ | (8) |
| $ \left\{ \sigma \right\} = [c](\left\{ \varepsilon \right\} - \left\{ {{\varepsilon _0}} \right\}) $ | (9) |
式中:σ为总应力;ε为总应变;ε0为初始应变;u为位移;F为荷载。
在冻土应变计算中,需对瞬态应变εe、水分的相变和迁移引起的土体应变εv进行考虑。
| $ \varepsilon = {\varepsilon ^{\text{e}}} + {\varepsilon _{\text{v}}} $ | (10) |
其中由水分相变和迁移产生的应变:
| $ {\varepsilon _{\text{v}}} = 0.09({\theta _0} + \Delta \theta - {\theta _{\text{u}}}) + \Delta \theta + ({\theta _0} - n) $ | (11) |
式中:θu为冻土中未冻水的体积含量(%);θ0为冻土中未冻水的初始体积含量(%);θ为冻土中水的体积含量(%)
1.3.5 PDE偏微分方程求解本研究选取固液比BI作为关键耦合项,其核心在于揭示未冻水含量随温度变化的内在规律:
| $ {B_{\text{I}}} = \frac{{{\theta _{\text{I}}}}}{{{\theta _{\text{u}}}}} = \left\{ {\begin{array}{*{20}{c}} {1.1{{\left( {\frac{T}{{{T_{\text{f}}}}}} \right)}^B} - 1}&{T < {T_{\text{f}}}}&{} \\ 0&{T \geqslant {T_{\text{f}}}}&{} \end{array}} \right. $ | (12) |
式中:Tf为土体冻结温度(K);θI为孔隙冰体积含量(%);θu为冻土中未冻水的体积含量(%)。固液比相关系数B为随土质类型及含盐量变化的常数,一般取值0.56。选用Van Genuehten(VG)滞水模型和Gardner渗透系数模型,将冻土的相对饱和度S定义为:
| $ S = \frac{{{\theta _{\text{u}}} - {\theta _{\text{r}}}}}{{{\theta _{\text{s}}} - {\theta _{\text{r}}}}} $ | (13) |
式中:θr和θs分别代表土体的残余含水率(cm3/cm3)和饱和含水率(cm3/cm3)。
进一步将温度场及水分场高度非线性方程组转化成系数型标准形式,温度场PDE方程,将公式(13)代入公式(1):
| $ \frac{{\partial {\theta _{\text{I}}}}}{{\partial t}} = \frac{{\partial \left( {B(T) \cdot {\theta _{\text{u}}}} \right)}}{{\partial t}} = \frac{{\partial \left( {B(T) \cdot \left( {\left( {{\theta _{\text{s}}} - {\theta _{\text{r}}}} \right)S + {\theta _{\text{r}}}} \right)} \right)}}{{\partial t}} = \left( {{\theta _{\text{s}}} - {\theta _{\text{r}}}} \right) \cdot \left( {\frac{{\partial B(T)}}{{\partial t}} \cdot S + B(T) \cdot \frac{{\partial S}}{{\partial t}}} \right) + {\theta _r}\frac{{\partial B(T)}}{{\partial t}} $ | (14) |
| $ \rho C(\theta )\frac{{\partial T}}{{\partial t}} + \nabla \cdot ( - \lambda (\theta )\nabla T) = L \cdot {\rho _{\text{I}}} \cdot \left[ {\left( {{\theta _{\text{s}}} - {\theta _{\text{r}}}} \right) \cdot \left( {\frac{{\partial B(T)}}{{\partial T}}\frac{{\partial T}}{{\partial t}} \cdot S + B(T) \cdot \frac{{\partial S}}{{\partial t}}} \right) + {\theta _{\text{r}}}\frac{{\partial B(T)}}{{\partial T}}\frac{{\partial T}}{{\partial t}}} \right] $ | (15) |
| $ \left( {\rho C(\theta ) - L \cdot {\rho _{\text{I}}} \cdot \left[ {\left( {{\theta _{\text{s}}} - {\theta _{\text{r}}}} \right) \cdot S + {\theta _{\text{r}}}} \right] \cdot \frac{{\partial B(T)}}{{\partial T}}} \right)\frac{{\partial T}}{{\partial t}} + \nabla \cdot ( - \lambda (\theta )\nabla T) = L \cdot {\rho _{\text{I}}} \cdot \left( {{\theta _{\text{s}}} - {\theta _{\text{r}}}} \right) \cdot B(T) \cdot \frac{{\partial S}}{{\partial t}} $ | (16) |
| $ {e_{\text{a}}}\frac{{{\partial ^2}T}}{{\partial {t^2}}} + {d_{\text{a}}}\frac{{\partial T}}{{\partial t}} + \nabla \cdot ( - c\nabla T - \alpha T + \gamma ) + \beta \cdot \nabla T + aT = f $ | (17) |
| $ \left\{ {\begin{array}{*{20}{l}} {{d_{\text{a}}} = \rho C(\theta ) - L \cdot {\rho _{\text{I}}} \cdot \left[ {\left( {{\theta _{\text{s}}} - {\theta _{\text{r}}}} \right) \cdot S + {\theta _{\text{r}}}} \right] \cdot \frac{{\partial B(T)}}{{\partial T}}} \\ {c = \lambda (\theta )} \\ {f = L{\rho _{\text{I}}} \cdot \left( {{\theta _{\text{s}}} - {\theta _{\text{r}}}} \right) \cdot B(T) \cdot \frac{{\partial S}}{{\partial t}}} \end{array}} \right. $ | (18) |
水分场PDE方程,将公式(13)代入公式(2):
| $ \frac{{\partial S}}{{\partial t}} + \frac{{{\rho _{\text{I}}}}}{{{\rho _{\text{w}}}}} \cdot \left[ {\left( {\frac{{\partial B(T)}}{{\partial t}} \cdot S + B(T) \cdot \frac{{\partial S}}{{\partial t}}} \right) + \frac{{{\theta _{\text{r}}}}}{{\left( {{\theta _{\text{s}}} - {\theta _{\text{r}}}} \right)}}\frac{{\partial B(T)}}{{\partial t}}} \right] = \nabla [D(S)\nabla S + k(S)] $ | (19) |
| $ \left( {1 + \frac{{{\rho _{\text{I}}}}}{{{\rho _{\text{w}}}}}B(T)} \right)\frac{{\partial S}}{{\partial t}} + \frac{{{\rho _{\text{I}}}}}{{{\rho _{\text{w}}}}} \cdot \frac{{\partial B(T)}}{{\partial t}} \cdot S + \frac{{{\rho _{\text{I}}}}}{{{\rho _{\text{w}}}}} \cdot \frac{{{\theta _{\text{r}}}}}{{\left( {{\theta _{\text{s}}} - {\theta _{\text{r}}}} \right)}}\frac{{\partial B(T)}}{{\partial t}} = \nabla [D(S)\nabla S + k(S)] $ | (20) |
| $ {e_{\text{a}}}\frac{{{\partial ^2}S}}{{\partial {t^2}}} + {d_{\text{a}}}\frac{{\partial S}}{{\partial t}} + \nabla \cdot ( - c\nabla S - \alpha S + \gamma ) + \beta \cdot \nabla S + aS = f $ | (21) |
| $ \left\{ {\begin{array}{*{20}{l}} {{d_{\text{a}}} = 1 + \frac{{{\rho _{\text{I}}}}}{{{\rho _{\text{w}}}}}B(T)} \\ {c = D(S)} \\ {\gamma = - k(S)} \\ \begin{gathered} a = \frac{{{\rho _{\text{I}}}}}{{{\rho _{\text{w}}}}} \cdot \frac{{\partial B(T)}}{{\partial t}} \hfill \\ f = - \frac{{{\rho _{\text{I}}}}}{{{\rho _{\text{w}}}}} \cdot \frac{{{\theta _{\text{r}}}}}{{\left( {{\theta _{\text{s}}} - {\theta _{\text{r}}}} \right)}}\frac{{\partial B(T)}}{{\partial t}} \hfill \\ \end{gathered} \end{array}} \right. $ | (22) |
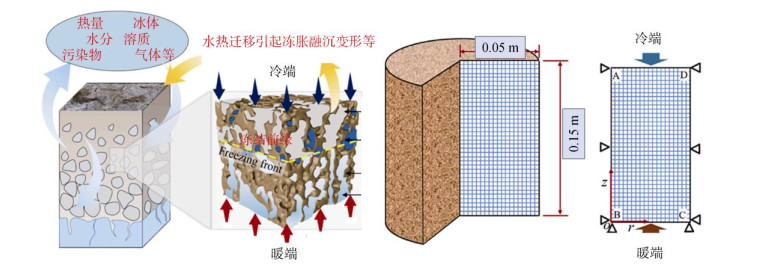
大气温度的周期性变化驱动表层地温同步响应,形成冻胀–融沉循环的核心驱动机制(图 3)。温度梯度引发未冻水定向迁移,促使含水率重分布,并通过导热系数(λ)和体积热容(C)等时变参数重构温度场,形成热–水耦合作用链。
|
图 3 冻融区土体水热迁移分布概念模型及试件模型尺寸 Fig. 3 Conceptual model of hydrothermal migration distribution in soil during freeze-thaw cycles and specimen model dimensions |
另外,冻融锋面的推进促使水分向相变界面富集,伴随相变潜热释放/吸收的热质传输过程,导致温度场与水分场呈现动态互馈关系。这种互馈效应通过改变土体孔隙结构(孔隙比e)与冰透镜体发育模式,继而影响有效应力分布。同时,应力场演变通过调控土体导热特性与渗透性能,反向约束温度场与水分场的时空演变,构成完整的水–热–力三场耦合系统。本研究构建的水热迁移机制模型及试样几何参数如图 3所示[27],模型参数如表 2所示。
|
|
表 2 模型参数 Table 2 Model parameters |
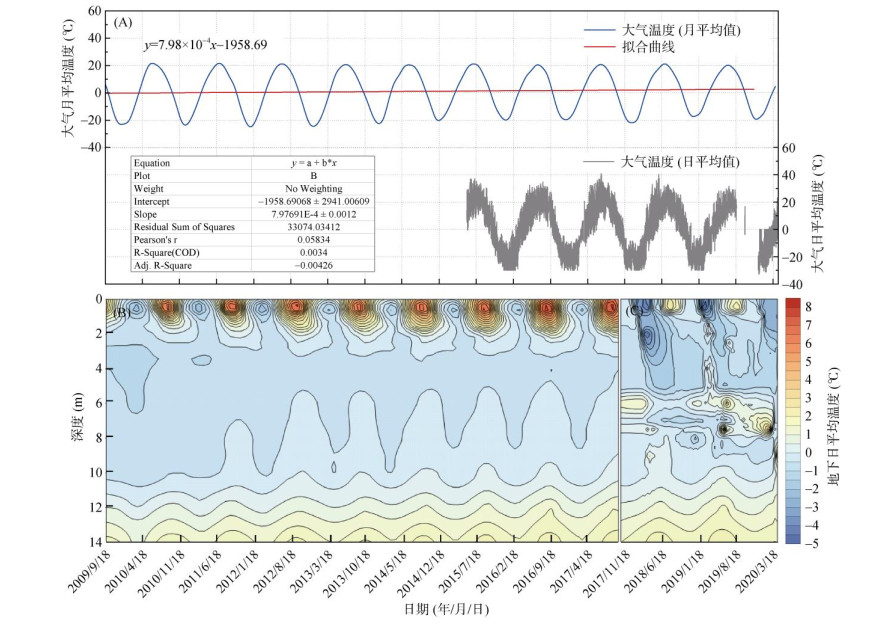
研究区位于多年冻土与季节性冻土过渡带,气候变暖及工程扰动加速了多年冻土退化。2009—2020年大气温度监测数据(图 4A)显示,月均温呈缓慢上升趋势,且与拟合曲线趋势一致。地温响应呈现显著季节性波动,峰值出现于每年9月,并随土层深度增加逐渐衰减(图 4B)。地温等值线图(图 4C)进一步揭示,研究区冻土退化表现为上下限同步异向迁移:下限上升速率(年均0.21 m)显著高于上限下降速率(年均0.07 m),冻融循环频次增加32% ~ 45%,表明冻土热稳定性持续弱化。
|
图 4 研究区A气象监测数据(大气温度及地温变化等值线图) Fig. 4 Meteorological monitoring data in study area-A (air temperature and geothermal contour map) |
为进一步分析不同深度土体结构对冻融过程的水热影响,在研究区开展多处钻探,基于4组钻孔的32组分层样本(部分土样见表 3)与现场实测数据,揭示不同深度土体结构对冻融水热过程的控制机制。
|
|
表 3 研究区A各钻孔位置不同深度的土样 Table 3 Soil samples at different depths of each drilling location in study area-A |
1) 表层草炭土及黑土的高冻胀性驱动水分重分布。1号钻孔0 ~ 4 m草炭土冻胀率达8.2%(–15 ℃),冻结期含水量增幅达12.3%。XRD显示蒙脱石含量达9.5%,促进冰透镜体发育,导致含水量呈“S”型分布(表层4 m处含水量25.7%,对比6 m处18.4%)。
2) 中层粉质黏土与砾砂层的渗透差异性调控水热传递。2号钻孔3.5 m粉质黏土渗透系数(2.7× 10–5 cm/s)较3号钻孔4.6 m砾砂层(6.3×10-3 cm/s)低2个量级。测试结果显示砾砂层孔隙率(31.2%)显著高于粉质黏土(19.8%),导致热传导路径偏移15° ~ 23°。
3) 深层泥岩与砂岩的矿物组成抑制冻融变形。1号钻孔7.0 m细泥岩含火山岩屑(占比38%),其单轴抗压强度(12.7 MPa)是表层土的6.5倍。虽然蒙脱石含量达14.3%,但刚性骨架使冻融循环后孔隙比仅增加0.04(e=0.52→0.56),同时,刚性骨架限制冰晶扩展,团聚体破坏率低于表层。
综上,钻探及测试数据表明,黑土区冻融过程受多尺度因素控制:表层矿物活性与冻胀特性主导水分迁移(R²=0.83);中层渗透差异调控热传导方向(P < 0.01);深层岩土力学性质抑制变形扩展(应变能降低62%)。
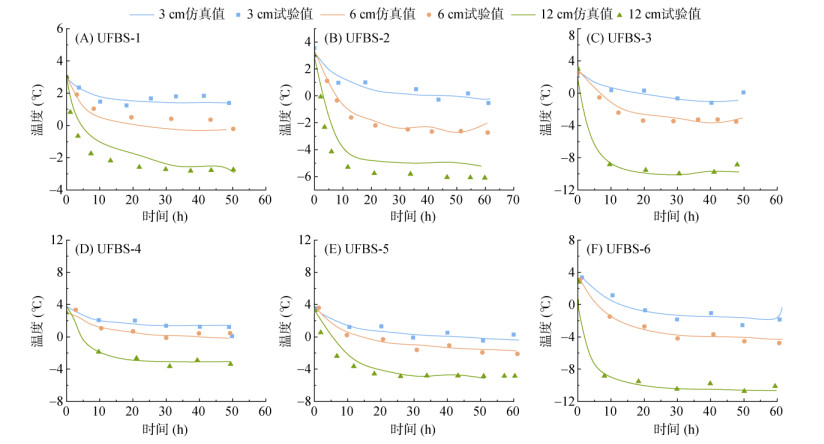
2.2 冻融作用下黑土水热及变形特性 2.2.1 试验验证本研究基于0 ~ 50 h单向冻结温度数据,用精度0.05 ℃的传感器进行分析。为避免冷热端边界效应,选取试件竖向距底部3、6和12 cm处的数据。通过热–水–变形多物理场模型与黑土试件单向冻结试验数据(部分引自文献[25])的定量和定性对比校验模型可靠性。温度及含水量仿真值与试验值对比结果见图 5和图 6。
|
图 5 不同深度单向冻结温度仿真值和试验值对照曲线 Fig. 5 Simulated and tested temperatures at different depths during unidirectional freezing |
|
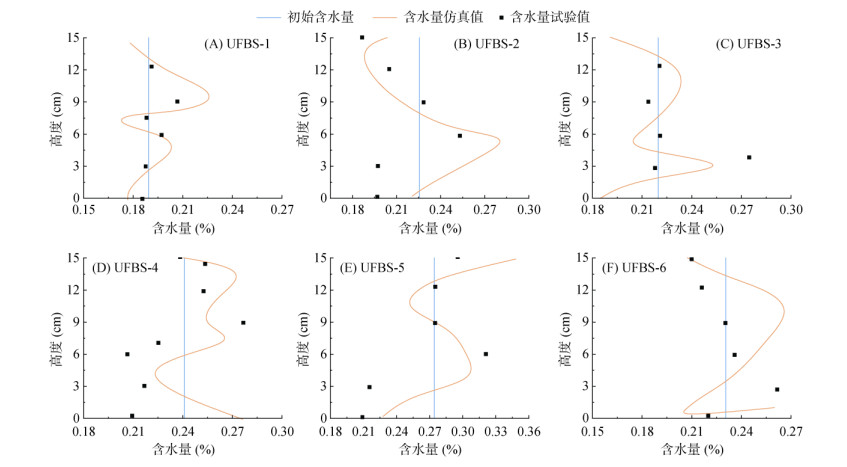
图 6 不同高度单向冻结过程含水量仿真值和试验值对照曲线 Fig. 6 Simulated and tested water contents at different hights during unidirectional freezing |
图 5显示不同深度(3、6、12 cm)单向冻结温度仿真值与试验值对照曲线,各深度温度曲线高度一致,冻结初期(0 ~ 10 h)和稳定冻结阶段(30 ~ 50 h),仿真模型能准确捕捉温度变化动态特征。图 6为不同高度点单向冻结过程最终含水量仿真值与试验值对比曲线。初始高含水量区域和最终稳定冻结区的含水量仿真值与试验值吻合较好,中间过渡区存在微小偏差,可能与冰水相变潜热动态分配差异有关。
为进一步验证模型精度,采用SPSS Statistics对同一时间不同深度的温度和含水量数据进行Pearson相关性分析(表 4、表 5)。温度仿真值与试验值的相关系数均值为0.919 ~ 0.959(表 4),含水量相关系数均值为0.708 ~ 0.816(表 5),均通过α=0.01显著性检验。结果表明,模型能有效表征黑土水热变形的时空分布特征,突变点与试验数据一致,适用于后续冻融过程模拟。
|
|
表 4 不同试件单向冻结温度试验值及仿真值相关系数 Table 4 Correlation coefficients between tested and simulated values of unidirectional freezing temperatures at different depths |
|
|
表 5 不同试件含水量试验值及仿真值相关系数 Table 5 Correlation coefficients between tested and simulated water contents at different depths |
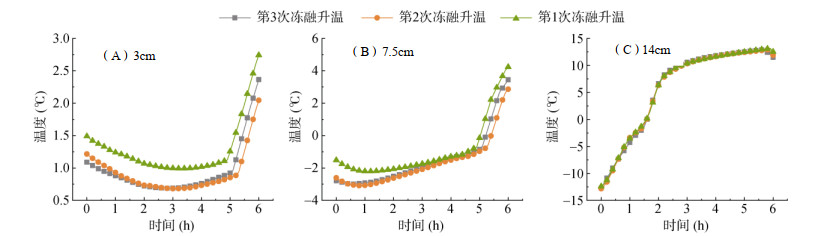
升温阶段:以试件CFBS-1为例,不同测点高度(3、7.5、14 cm)3次冻融升温曲线如图 7所示。升温阶段(5 ~ 11 h第1次冻融、17 ~ 23 h第2次冻融、29 ~ 35 h第3次冻融)显示,靠近冻融端的14 cm处温度响应更敏感(图 7C),升温速率显著高于底部3 cm和7.5 cm处。例如,第一次冻融时,14 cm处初始升温速率为8 ℃/h,而3 cm处因热量传递滞后,仍处于降温阶段。
|
图 7 不同高度三次冻融过程中升温变化曲线 Fig. 7 Temperature rise curves during three freeze-thaw cycles at different heights |
相变热力学分析表明,升温过程的阶段性特征(快–缓–快–缓)与冰晶融化吸热相关。当温度接近相变点(–0.56 ℃)时,潜热吸收导致升温速率下降(图 7C)。此外,第三次冻融升温温度整体高于前两次,但速率略低,这与冻融循环中水分迁移引起的比热差异有关。
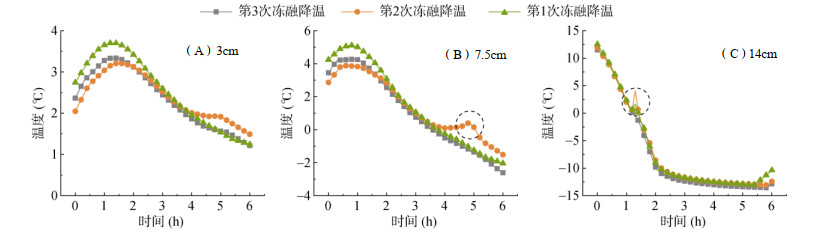
降温阶段:图 8显示不同高度3次冻融降温曲线(11 ~ 17 h第1次冻融、23 ~ 29 h第2次冻融、35 ~ 41 h第3次冻融)。靠近冻融端的14 cm处降温速率最快,而底部3 cm和7.5 cm处因热量传递滞后,初期呈现短暂升温后呈降温趋势。随冻融循环次数增加,高温阶段温度逐渐降低(3 cm处:3.75 ℃→3.27 ℃),低温阶段温度略升(1.24 ℃→1.26 ℃),反映了水分迁移对区域热容的累积影响。
|
图 8 不同高度三次冻融过程中降温变化曲线 Fig. 8 Temperature drop curves during three freeze-thaw cycles at different heights |
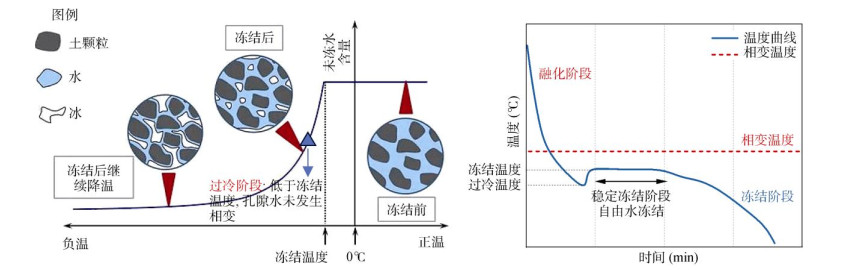
另外,在温度降低到相变点(–0.56 ℃)会出现温度上下波动,这与冻结过程过冷等现象有关,表层相变过冷度达1.2 ~ 2.5 ℃。通过图 8和图 9可以看出,土体冻结主要分为5个阶段:冷却阶段,温度降至冰点(0 ℃),未形成冰相;过冷阶段,温度降至–1.2 ~ –2.5 ℃,自由水维持过冷态;温度突升阶段,冰晶成核释放潜热,温度回升至冰点;稳定冻结阶段,温度恒定,冰相持续扩展;冻土强化阶段,温度进一步下降,冻土强度递增。
|
图 9 土体冻结过程温度–时间曲线及过冷现象 Fig. 9 Temperature-time curve and supercooling phenomenon during soil freezing |
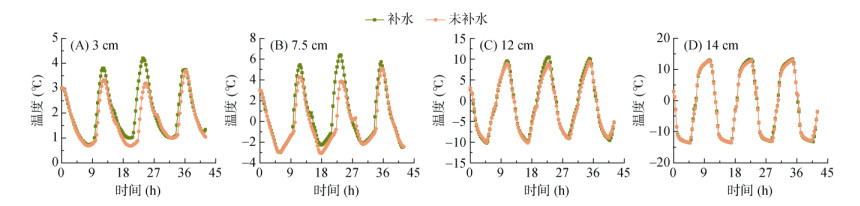
图 10对比了补水与未补水条件下各高度(3、7.5、12、14 cm)的温度变化。结果表明:3 cm和7.5 cm处,补水条件下整体温度较未补水高2 ~ 4 ℃,且冻深减少28% ~ 35%,表明水分补给可削弱地表负温效应(图 10A、10B);12 cm处,降温阶段两者温度趋近,但补水条件下升温阶段温度略高(图 10C);14 cm处,3次冻融升降温曲线基本重叠,表明补水对表层温度影响较小(图 10D)。机理分析表明,补水通过毛细作用向上层输水,增加未冻水含量,提升土体热容,从而延缓冻结速率并提高升温阶段温度;而未补水条件下,水分迁移受限,冻胀量随温度变化速率减缓而增大。
|
图 10 不同补水条件下各高度温度变化情况 Fig. 10 Temperature variations at different depths under different water replenishment conditions |
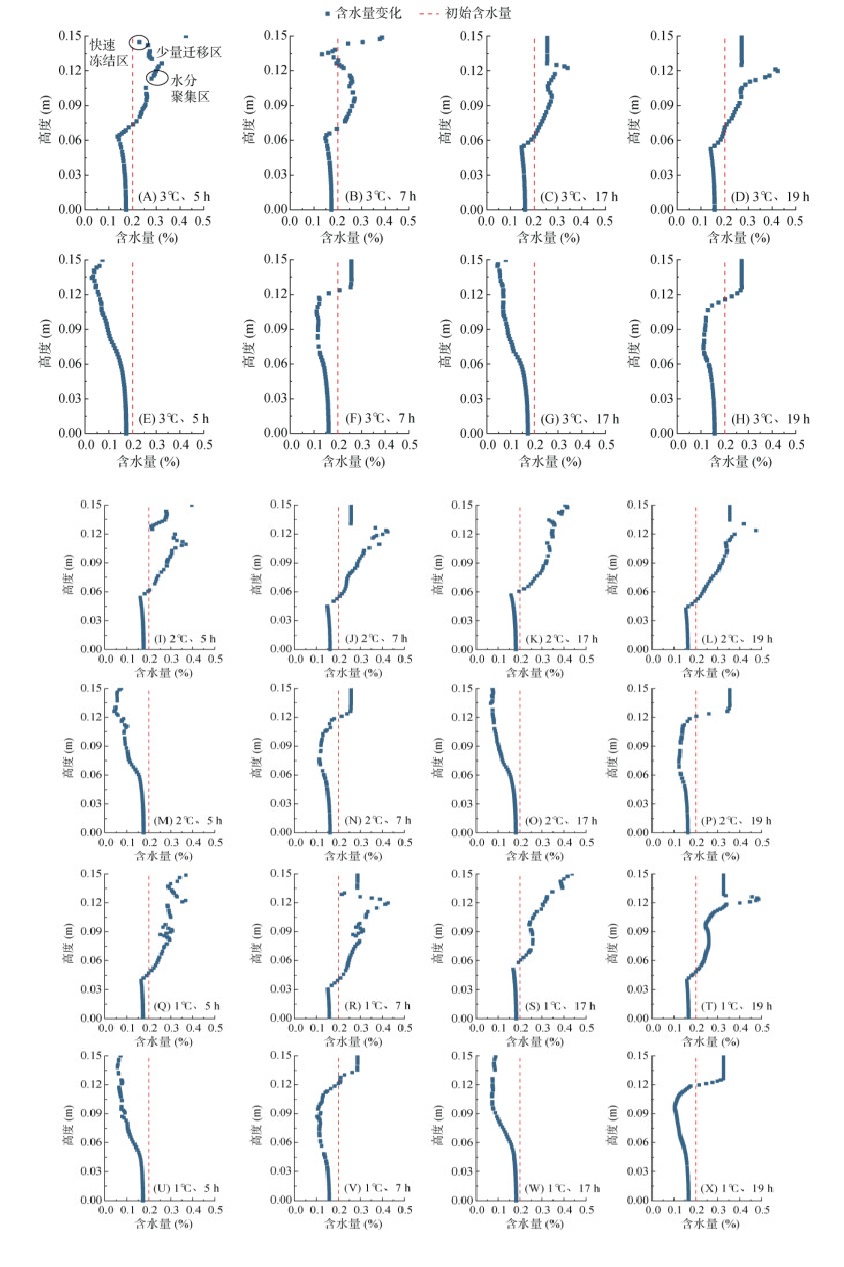
图 11为不同初始温度(1、2、3 ℃)及冻融阶段下总含水量和未冻水含量的竖向分布特征。冻结过程结束后,水分场表现出显著的重新分布现象,各试样的总含水量均呈现“S”型分布特征。
|
(图A ~ D、I ~ L、Q ~ T为总含水量;E ~ H、M ~ P、U ~ X为未冻水含量) 图 11 不同初始温度及冻融阶段总含水量和未冻水含量竖向分布特征 Fig. 11 Vertical distributions of total and unfrozen water contents at different initial temperatures and freeze-thaw stages |
总含水量整体呈上高下低趋势(图 11A ~ D、I ~ L、Q ~ T),根据水分迁移速率差异,可将土层自上而下划分为:快速冻结区(靠近冷端),温度梯度大,水分原位冻结为主,迁移受限;少量迁移区(中部),降温速率减缓,未冻水部分迁移;水分积聚区(远离冷端),温度稳定,未冻水在低负温下缓慢冻结,迁移剧烈,含水量达峰值。随着冻融循环次数增加,下部水分逐渐向中上部迁移,表明冻结过程中水分受温度梯度驱动发生定向迁移。
未冻水含量呈自下而上逐渐降低趋势(图 11E ~ H、M ~ P、U ~ X),主要源于上部冷端低温向下传递形成的温度梯度。融化阶段,上部温度升高导致热流方向反转,未冻水含量在冷端附近显著增加。且距离冷端越近的土层,降温速率越大,冻结锋面移动越快,冰水界面热状态越不稳定,未冻水迁移时间越短,迁移量越小。
另外,初始温度对冻结后水分场分布趋势影响较小,但初始温度较低的土柱(如1 ℃)最大含水量略高于初始温度较高的土柱(如3 ℃)。这归因于低温条件下相变时间延长,水分迁移条件更优。
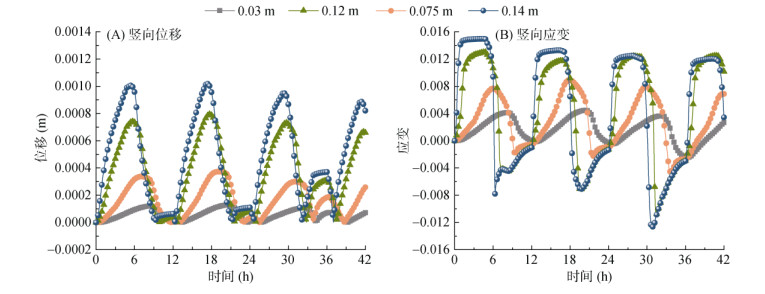
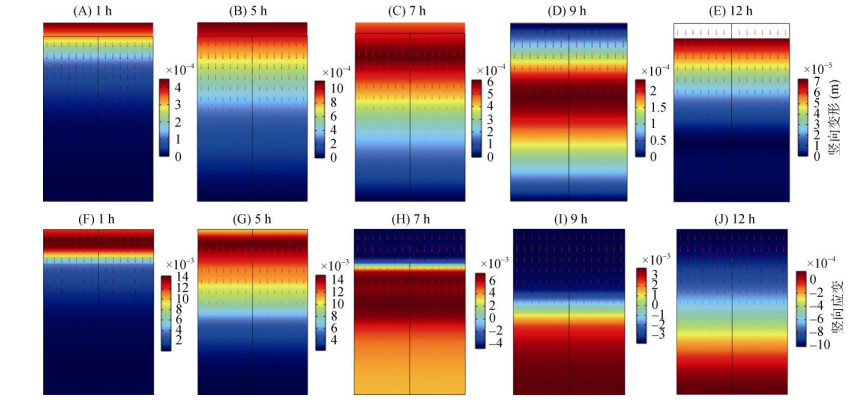
2.2.5 考虑补水冻融过程宏观竖向形变特征图 12和图 13分别为补水下冻融过程的竖向位移和应变曲线及其云图,其中竖向位移变化规律(图 12A、图 13A ~ E):冻胀变形沿试件高度递增,冷端附近(0.14 m高度)变形最大(第一次冻融达0.001 1 m),而远离冷端处(0.03 m高度)变形最小(0.000 11 m)。温度传递滞后性导致冷端区更早达到最大冻胀变形。随冻融循环次数增加,最大冻胀变形呈递减趋势(如0.14 m处:第1次0.001 1 m→第4次0.000 89 m),表明土体结构因反复冻融逐渐密实,水分迁移能力减弱。
|
图 12 考虑补水冻融过程竖向位移及应变曲线 Fig. 12 Vertical displacement and strain curves during freeze-thaw cycles with water replenishment |
|
(图A ~ E为竖向变形云图;F ~ J为应变云图) 图 13 考虑补水冻融过程竖向位移及应变云图 Fig. 13 Vertical displacement and strain contour maps during freeze-thaw cycles with water replenishment |
针对应变变化规律(图 12B、图 13F ~ J):应变分布与位移一致,冷端附近正应变最大(第一次冻融达0.014 5),随冻融次数增加,正应变减小,负应变增大(如0.14 m处:正应变第1次0.014 5→第3次0.012 5;负应变第1次–0.008 1→第3次–0.012 4)。这一现象反映了土体在冻胀阶段因冰晶生长产生拉应力,融沉阶段因冰融化和孔隙塌缩产生压应力的动态响应。
形变动力学分析表明,补水条件下,水分补给加剧了冻胀效应,但多次冻融循环后,土体内部孔隙结构因冰晶反复生成-融化而逐渐重组,导致迁移通道堵塞,冻胀潜力下降。此外,热滞后效应和温度梯度非线性分布是形变空间异质性的核心驱动因素。
2.2.6 冻融过程微观形变及团聚体破碎特征进一步通过扫描电镜(SEM)对初始含水量为3.4%、32.3% 及43.4% 的黑土样本进行观测(图 14),发现冻融循环显著改变其微观孔隙结构。低含水量样本(3.4%):未冻融时,颗粒镶嵌紧密,微裂缝与孔隙清晰可见(天然损伤);5次冻融后,大颗粒破碎重组;30次冻融后,小颗粒填充孔隙,土体松散,结构破坏。这表明低含水量条件下,冻融主要通过机械破碎改变颗粒分布,但整体结构稳定性较高。

|
图 14 不同含水量及冻融次数下代表性黑土扫描电镜(SEM)图像 Fig. 14 Representative scanning electron microscope (SEM) images of soil samples with different water contents and freeze-thaw cycles |
中高含水量样本(32.3% 和43.4%):未冻融时,颗粒边界模糊,孔隙难辨;随着冻融次数增加,5次冻融后,孔隙显现,颗粒圆润化,破碎重组显著;30次冻融后,微孔洞数量剧增,呈伸长、交叉及贯通形态,次生孔隙发育,土体逐渐疏松,其中高含水量样本(43.4%)因水分冻胀效应更强,孔隙扩展更剧烈。
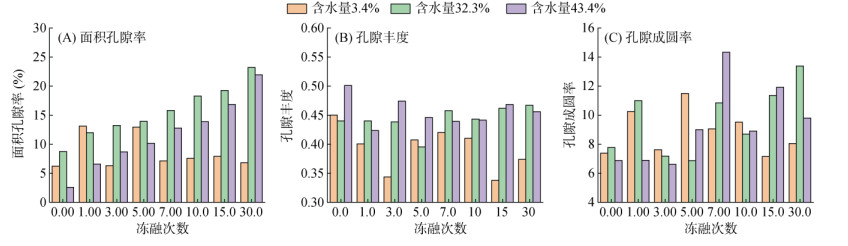
图 15A为不同冻融循环次数后面积孔隙率变化特征,其中初始孔隙率为5.73%(初始含水量3.4%)、8.75%(初始含水量32.3%)、2.52%(初始含水量43.4%);30次冻融后,孔隙率分别增至6.97%、23.14%、22.18%,增长率分别达21.62%、164.36%、546.47%。可以看出,初始含水量越高,冻融对孔隙率的提升效应越显著(初始含水量43.4% 样本因冻胀主导,孔隙扩展幅度最大)。
|
图 15 不同冻融次数下土体结构参数变化 Fig. 15 Changes in soil structure parameters after different freeze-thaw cycles |
图 15B、15C为不同冻融循环次数后孔隙丰度和孔隙成圆率变化特征,用以定量描述孔隙形态。其中孔隙丰度(反映形状规则性)表现为:随冻融次数增加,丰度下降(初始含水量3.4% 样本降幅最大,达17.80%),表明孔隙趋向狭长化(冰晶劈裂沿长轴扩展)。孔隙成圆率(反映颗粒圆度)表现为:短期冻融(7次),成圆率显著上升(初始含水量43.4% 样本增长率达113.92%),因颗粒棱角被冻融应力磨圆;长期冻融(30次),成圆率下降,孔隙轮廓不规则化(冰晶反复冻胀导致颗粒二次破碎)。
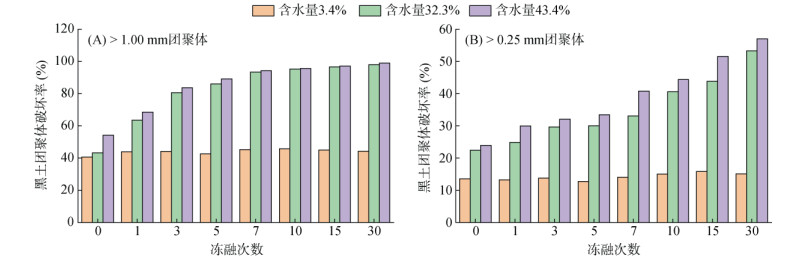
图 16为不同含水量及冻融次数下黑土团聚体破坏率,可以看出:对于团聚体 > 1.00 mm(粗颗粒),高含水量样本(43.4%)的初始破坏率达54.2%,显著高于低含水量样本(3.4%)的40.7%。另外,破坏率冻融响应随冻融次数快速上升(5次冻融后达89.2%,30次后达99.0%),其中10次冻融后增速趋缓。这是由于高含水量下冰晶生长产生膨胀应力,直接破坏大颗粒间连接。
|
图 16 不同含水量及冻融次数下黑土团聚体破坏率 Fig. 16 Soil aggregate destruction rates under different water contents and freeze-thaw cycles |
对于团聚体 > 0.25 mm(细颗粒),高含水量(43.4%)样本的初始破坏率为23.9%,低含水量(3.4%)样本仅13.6%。破坏率冻融响应持续上升(30次冻融后达57.0%),但增幅低于粗颗粒,表明细颗粒抗冻融能力较强。所以高含水量(> 32.3%)显著加剧冻融对团聚体的破坏,尤其是粗颗粒;10次冻融为团聚体破坏速率转折点,后续破坏趋于饱和。
3 结论1) 未补水条件下,黑土冻结后总含水量呈“S”型分布,未冻水含量自上而下递减;补水通过提升热容削弱地表负温效应,冻深减少28% ~ 35%;冻融锋面推进受温度梯度与相变潜热动态调控,表层相变过冷度达1.2 ~ 2.5 ℃,温度传递滞后性显著。
2) 冻胀变形沿试件高度递增,冷端附近(0.14 m)最大位移达0.001 1 m;多次冻融后土体密实化,冻胀潜力下降;高含水量(> 32.3%)样本孔隙率增长546.47%,团聚体破坏率高达99%,表明水分是冻融侵蚀的核心驱动因素。
3) 表层草炭土与黑土的高冻胀性需通过秸秆覆盖或排水措施抑制水分迁移;中层渗透差异(如粉质黏土与砾砂层)要求工程中需优化填料级配,避免滞水引发热传导偏移;深层细泥岩的刚性骨架可为土基稳定层设计提供参考。
4) 构建的热-水-变形多场耦合模型(相关系数 > 0.9)可精准预测黑土冻融响应,为寒区农业保墒与工程防冻设计提供理论支撑;建议寒区农田采用低含水量耕作制度,并建立动态监测体系以预警冻融侵蚀风险。
| [1] |
沈海鸥, 任明, 温磊磊, 等. 黑土区坡耕地水力侵蚀及其防治技术研究进展[J]. 灌溉排水学报, 2024, 43(10): 97-105 (  0) 0) |
| [2] |
穆青, 夏淑媛, 李庆阳, 等. 不同秸秆还田方式对典型砂姜黑土收缩特征的影响[J]. 土壤, 2024, 56(5): 1084-1090 DOI:10.13758/j.cnki.tr.2024.05.020 (  0) 0) |
| [3] |
赵显波, 刘振平, 许士国, 等. 季节冻土区黑土耕层土壤冻融循环期湿度与温度变化研究[J]. 冰川冻土, 2015, 37(4): 931-939 (  0) 0) |
| [4] |
Li P, Ying D, Li J, et al. Global-scale no-tillage impacts on soil aggregates and associated carbon and nitrogen concentrations in croplands: A meta-analysis[J]. Science of The Total Environment, 2023, 881: 163570 DOI:10.1016/j.scitotenv.2023.163570 (  0) 0) |
| [5] |
El Harche S, Chikhaoui M, Naimi M, et al. No-tillage and agroforestry decrease sediment loss from a hilly landscape in northern Morocco[J]. Catena, 2023, 223: 106951 DOI:10.1016/j.catena.2023.106951 (  0) 0) |
| [6] |
王恩姮, 卢倩倩, 陈祥伟. 模拟冻融循环对黑土剖面大孔隙特征的影响[J]. 土壤学报, 2014, 51(3): 490-496 (  0) 0) |
| [7] |
Huang D H, Su L, Zhou L L, et al. Gully is the dominant sediment source of snowmelt erosion in the black soil region–A case study[J]. Soil and Tillage Research, 2022, 215: 105232 DOI:10.1016/j.still.2021.105232 (  0) 0) |
| [8] |
黄伟根, 倪浩为, 黄瑞林, 等. 不同气候条件下土壤有机碳水热响应驱动机制研究[J]. 土壤学报, 2024, 61(5): 1260-1270 (  0) 0) |
| [9] |
赵露, 叶含春, 王振华, 等. 基于SHAW模型的北疆地区不同滴灌年限棉田冻融期土壤水热盐动态模拟研究[J]. 土壤, 2024, 56(3): 623-638 DOI:10.13758/j.cnki.tr202307050260 (  0) 0) |
| [10] |
张茜, 马仁明, 贾燕锋, 等. 冻融对典型黑土团聚体输移破碎特征的影响[J]. 应用生态学报, 2024, 35(5): 1275-1282 (  0) 0) |
| [11] |
Dai Z G, Fei L J, Huang D L, et al. Coupling effects of irrigation and nitrogen levels on yield, water and nitrogen use efficiency of surge-root irrigated jujube in a semiarid region[J]. Agricultural Water Management, 2019, 213: 146-154 DOI:10.1016/j.agwat.2018.09.035 (  0) 0) |
| [12] |
Ban Y Y, Lei T W, Liu Z Q, et al. Comparative study of erosion processes of thawed and non-frozen soil by concentrated meltwater flow[J]. Catena, 2017, 148: 153-159 DOI:10.1016/j.catena.2016.06.019 (  0) 0) |
| [13] |
Rui D H, Zhai J B, Li G Y, et al. Field experimental study of the characteristics of heat and water transfer during frost heaving[J]. Cold Regions Science and Technology, 2019, 168: 102892 DOI:10.1016/j.coldregions.2019.102892 (  0) 0) |
| [14] |
孙国静, 卞建民, 王宇, 等. 东北典型黑土区积雪-冻融耦合作用下的包气带水热运移模拟[J]. 吉林农业大学学报, 2024, 46(2): 306-314 (  0) 0) |
| [15] |
王文刚, 王彬, 顾汪明, 等. 冻融循环对黑土团聚体稳定性与微结构特征的影响[J]. 水土保持学报, 2022, 36(1): 66-73 (  0) 0) |
| [16] |
刘乃飞, 李宁, 汪双杰, 等. 含相变低温岩体水–热–力特性研究进展与展望[J]. 岩石力学与工程学报, 2025, 44(3): 521-542 (  0) 0) |
| [17] |
刘红希, 范昊明, 许秀泉. 黑土冻融过程中水分垂直迁移模拟研究[J]. 水土保持学报, 2021, 35(1): 169-173 (  0) 0) |
| [18] |
Lai Y M, Liu S Y, Wu Z W, et al. Numerical simulation for the coupled problem of temperature and seepage fields in cold region dams[J]. Journal of Hydraulic Research, 2002, 40(5): 631-635 DOI:10.1080/00221680209499907 (  0) 0) |
| [19] |
Wang C, Ma Z P. Mathematical model and numerical simulation of hydrothermal coupling for unsaturated soil subgrade in the seasonal frozen zone[J]. IOP Conference Series: Earth and Environmental Science, 2021, 719(3): 032042 DOI:10.1088/1755-1315/719/3/032042 (  0) 0) |
| [20] |
Huang X, Rudolph D L. Coupled model for water, vapour, heat, stress and strain fields in variably saturated freezing soils[J]. Advances in Water Resources, 2021, 154: 103945 DOI:10.1016/j.advwatres.2021.103945 (  0) 0) |
| [21] |
何瑞霞, 金会军, 赵淑萍, 等. 冻土导热系数研究现状及进展[J]. 冰川冻土, 2018, 40(1): 116-126 (  0) 0) |
| [22] |
Bai R Q, Lai Y M, Zhang M Y, et al. Study on the coupled heat-water-vapor-mechanics process of unsaturated soils[J]. Journal of Hydrology, 2020, 585: 124784 DOI:10.1016/j.jhydrol.2020.124784 (  0) 0) |
| [23] |
Zhou J Z, Li D Q. Numerical analysis of coupled water, heat and stress in saturated freezing soil[J]. Cold Regions Science and Technology, 2012, 72: 43-49 DOI:10.1016/j.coldregions.2011.11.006 (  0) 0) |
| [24] |
蒋瑶钰, 王彬, 陈祖明, 等. 基于COMSOL模型的黑土农耕地剖面冻结水热耦合分析[J]. 水土保持学报, 2023, 37(6): 187-193 (  0) 0) |
| [25] |
陈祖明. 基于连通性和水热耦合作用的黑土坡面径流侵蚀阻控机制[D]. 北京: 北京林业大学, 2022.
(  0) 0) |
| [26] |
顾汪明. 冻融循环对东北黑土团聚体稳定性影响机制的研究[D]. 北京: 北京林业大学, 2020.
(  0) 0) |
| [27] |
Zhang J, Lai Y M, Zhang M Y, et al. Numerical study on the hydro-thermal-chemical–mechanical coupling mechanism in sulfate saline soil under freeze–thaw cycles[J]. Computers and Geotechnics, 2024, 176: 106803 DOI:10.1016/j.compgeo.2024.106803 (  0) 0) |
| [28] |
李雪冬, 红英, 费龙, 等. 中国东北黑土区地表土壤含水量时空分异特征研究[J]. 长春师范大学学报, 2024, 43(4): 92-100 (  0) 0) |
| [29] |
Dal Ferro N, Delmas P, Duwig C, et al. Coupling X-ray microtomography and mercury intrusion porosimetry to quantify aggregate structures of a cambisol under different fertilisation treatments[J]. Soil and Tillage Research, 2012, 119: 13-21 DOI:10.1016/j.still.2011.12.001 (  0) 0) |
2. Ministry of Education Northeast Permafrost Zone Geological Environment System Field Scientific Observation and Research Station, Northeast Forestry University, Harbin 150040, China;
3. Ministry of Water Resources Key Laboratory of River and Lake Source Area Water Ecological Management and Protection, Qinghai University, Xining 810016, China;
4. Hunan Provincial Research Center for Urban Underground Infrastructure Structural Safety and Disaster Prevention Engineering, Hunan City University, Yiyang, Hunan 413002, China;
5. Hunan Provincial Key Laboratory of Digital Urban and Rural Spatial Planning Technology, Hunan City University, Yiyang, Hunan 413002, China;
6. Heilongjiang Provincial Key Laboratory of Disaster Prevention and Mitigation Engineering and Protective Engineering in Colleges and Universities, Northeast Petroleum University, Daqing, Heilongjiang 163318, China;
7. Ministry of Education Key Laboratory of Structural Disaster and Control, Harbin Institute of Technology, Harbin 150040, China
 2025, Vol. 57
2025, Vol. 57


















